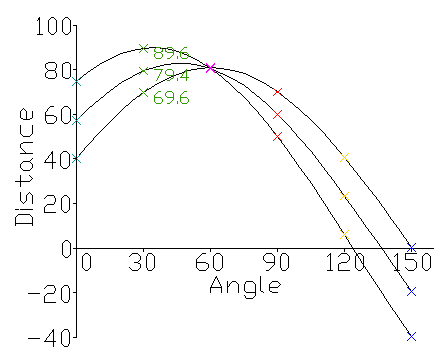
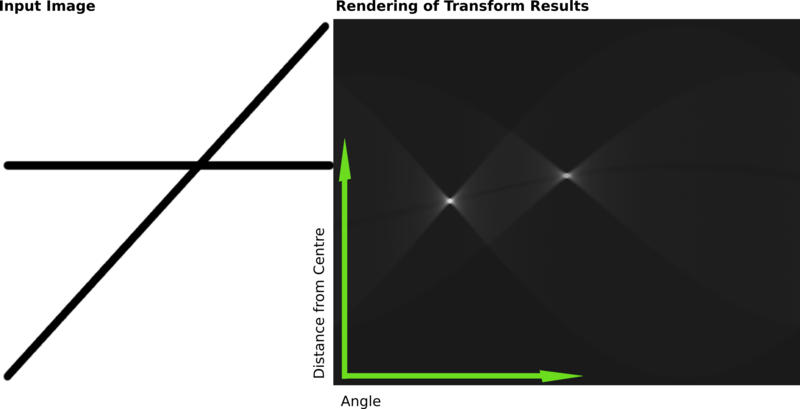
Преобразование Хафа
|
Read other articles:

Raja Mithridates atau Antiochus I dari Commagene berjabat tangan dengan Heracles Arsameia di Nymphaios (bahasa Armenia: Արշամաշատ, translit. Arshamashan; Turkish: Eski Kalecode: tr is deprecated – Kastil Lama) adalah sebuah kota kuno yang terletak di Kâhta Lama (Eski Kâhta), distrik Kâhta, Provinsi Adıyaman, Turki. Situs tersebut terletak di dekat Kâhtaçay, yang dikenal pada zaman kuno sebagai Nymphaios. Daftar pustaka Friedrich Karl Dörner, Theresa Goell: Arsameia ...

Map Sophene sebagai negara vasal Kerajaan Armenia Kerajaan Sophene (Armenian: Cop'khcode: hy is deprecated , bahasa Yunani Kuno: Σωφηνή, translit. Sōphēnē),[1] merupakan entitas politik era Helenistik yang terletak di antara Armenia kuno dan Suriah.[2] Dipimpin oleh Dinasti Orontid, kerajaan ini memiliki budaya campuran dengan pengaruh Yunani, Armenia, Iran, Syam, Anatolia dan Romawi.[3] Kerajaan Sophene didirikan pada sekitar abad ke-3 SM, kerajaan m...

Ekspedisi Manchu ke Tibet (1720)Bagian dari Peperangan Qing–DzungarTanggal1720LokasiTibetHasil Kemenangan Qing Tibet di bawah kekuasaan QingPihak terlibat Dinasti QingPolhanas (sekutu Qing)Kangchennas (sekutu Qing) Kekhanan DzungarTokoh dan pemimpin Kangxi EmperorYue Zhongqi [zh][1] (keturunan Yue Fei)Polhané Sönam TopgyéKhangchenné TagtsepaKekuatan Delapan PanjiTentara Standar Hijau Tentara Dzungar Bagian dari seri artikel mengenaiSejarah Tibet Neolitikum Tibet Zha...

Election to the European Parliament 2019 European Parliament election ← 2014 23–26 May 2019[1] 2024 → ← outgoing memberselected members →All 751 seats to the European Parliament376 seats needed for a majorityTurnout198,352,638 (50.66%[2] 8.01 pp) Leader Manfred Weber Frans Timmermans Margrethe Vestager Alliance EPP S&D Renew Leader's seat Germany Netherlands Denmark[a] Last election 221 seats, 23.8% 191...

Pour les articles homonymes, voir Matignon. Cet article est une ébauche concernant une commune des Côtes-d'Armor. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture du projet Communes de France est à votre disposition pour v...

Disambiguazione – Se stai cercando il batteriologo omonimo, vedi Antonio Carini (medico). Antonio Carini Antonio Carini (Monticelli d'Ongina, 7 settembre 1902 – Meldola, 13 marzo 1944) è stato un partigiano e antifascista italiano, noto col nome di battaglia di Orso e/o Orsi. Comunista, Garibaldino in Spagna, confinato politico, membro del Comando Generale delle Brigate Garibaldi, torturato e ucciso dai fascisti, Medaglia d'argento al valor militare alla memoria. Indice 1 Biografia 2 On...

Questa voce sull'argomento calciatori burkinabé è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Alassane Ouédraogo Nazionalità Burkina Faso Altezza 173 cm Calcio Ruolo Centrocampista Termine carriera 2012 Carriera Giovanili Santos Ouagadougou Squadre di club1 1996-2000 Charleroi54 (4)2000-2003 Colonia3 (0)2003-2005 RW Oberhausen60 (7)2005-2009 Coblenza24 (1)2010 Rot-Weiss Essen15 (0)2010-2012 Fortuna Coloni...

American judge Richard Stockton FieldJudge of the United States District Court for the District of New JerseyIn officeJanuary 14, 1863 – April 25, 1870Appointed byAbraham LincolnPreceded byPhilemon DickersonSucceeded byJohn T. NixonUnited States Senatorfrom New JerseyIn officeNovember 21, 1862 – January 14, 1863Appointed byCharles Smith OldenPreceded byJohn Renshaw ThomsonSucceeded byJames Walter Wall Personal detailsBornRichard Stockton Field(1803-12-31)December 31, 180...

Cape in the northeastern United States This article is about the area of Massachusetts. For other uses, see Cape Cod (disambiguation). Cape CodCapeCape Cod National SeashoreCape Cod (Barnstable County), in MassachusettsCoordinates: 41°41′N 70°12′W / 41.68°N 70.2°W / 41.68; -70.2LocationMassachusetts, United StatesOffshore water bodiesCape Cod BayBuzzards BayCape Cod CanalNantucket SoundArea • Total339 sq mi (880 km2)[1]Elevati...

Contea di HowardconteaLocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoBig Spring Data di istituzione1876 TerritorioCoordinatedel capoluogo32°18′36″N 101°26′24″W / 32.31°N 101.44°W32.31; -101.44 (Contea di Howard)Coordinate: 32°18′36″N 101°26′24″W / 32.31°N 101.44°W32.31; -101.44 (Contea di Howard) Superficie2 342 km² Abitanti35 012 (2010) Densità14,95 ab./km² Altre informazioni...

Азиатский барсук Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКласс:Мле�...

В Википедии есть статьи о других людях с фамилией Тимошина. Любовь Константиновна Слиска blank300.png|1px]] Заместитель председателя Государственной думы 24 декабря 2007 года — 21 декабря 2011 года Первый заместитель председателя Государственной думы 19 января 2000 года — 24 декаб...

Private liberal arts college in St. Peter, Minnesota, US Gustavus Adolphus CollegeFormer namesMinnesota Elementarskola (1862–1865)St. Ansgar's Academy(1865–1873)Gustavus Adolphus Literary & Theological Institute(1873–1876)MottoE Caelo Nobis Vires[1]Motto in EnglishStrength Comes To Us From HeavenTypePrivate liberal arts collegeEstablished1862; 162 years ago (1862)Religious affiliationEvangelical Lutheran Church in AmericaEndowment$281.6 million (2021)&...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) المقالات الرئيسة: الدين في العراق والإسلام في العراق جامع تكريت الكبير جامع أبو دلف. تحتوي محافظة صلاح ال...

Japanese knife Japanese kaiken-style tantō A kaiken (懐剣) is a 20–25 cm (7.9–9.8 in) long, single or (very rarely) double-edged Japanese knife[1] usually without ornamental fittings housed in a plain but lacquered mount. Uses The kaiken was once carried by men and women of the samurai class in Japan. It was useful for self-defense in indoor spaces where the long-bladed katana and intermediate-length wakizashi were inconvenient. Women carried them in their kimono eith...

This article is missing information about members elected for each party by province. Please expand the article to include this information. Further details may exist on the talk page. (February 2024) 1920 Indian general election 1920 1923 → 104 seats contested53 seats needed for a majority First party Second party Leader Hari Singh Gour W. H. H. Vincent Party DP Independent Seats won 48 47 This article is part of a series on the Politics of India Constitution a...

Swedish bishop The Most ReverendNathan SöderblomArchbishop of UppsalaPrimate of SwedenChurchChurch of SwedenDioceseUppsalaElected20 May 1914In office1914–1931PredecessorJohan August EkmanSuccessorErling EidemOrdersOrdination1893 (priest)Consecration8 November 1914by Gottfrid BillingPersonal detailsBornLars Olof Jonathan Söderblom(1866-01-15)15 January 1866Trönö, SwedenDied12 July 1931(1931-07-12) (aged 65)Uppsala, SwedenNationalitySwedishDenominationChurch of SwedenParentsJona...

2012 American cartoon anthology Looney Tunes Platinum Collection: Volume 2Directed byChuck Jones, Bob Clampett, Friz Freleng, Robert McKimson, Tex Avery, Arthur Davis, Ben Hardaway, Cal DaltonProduced byLeon Schlesinger, Eddie Selzer, John W. Burton, Fred Quimby (Disc 3 only)Starringvoice of Mel BlancMusic byNorman SpencerCarl StallingMilt FranklynScott Bradley (in Disc 3, Special features)Distributed byWarner Home VideoRelease date October 16, 2012 (2012-10-16) CountryUnited S...

Johnny Wahab Informasi pribadiLahir1950 (1950)Kotabumi, Lampung Utara, LampungMeninggal2 Juli 2012JakartaPartai politikGerindraSuami/istriDr. Hj. R.A. Evita Isretno Israhadi, S.H., M.H.Alma materAkademi Militer (1974)Karier militerPihak IndonesiaDinas/cabang TNI Angkatan DaratMasa dinas1974—2007Pangkat Mayor Jenderal TNISatuanInfanteriPertempuran/perangOperasi SerojaPemberontakan di AcehSunting kotak info • L • B Mayor Jenderal TNI (Purn.) Drs. H. Johnny Wahab, ...




![{\displaystyle \theta \in [0,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c833964ea08aa30df8b6f56664461a5499b38144)

![{\displaystyle \theta \in [0,2\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e90716b30df198360bcc41f8f9b230b76bf26163)