Подгруппа
|
Read other articles:

العلاقات البريطانية اللبنانية المملكة المتحدة لبنان المملكة المتحدة لبنان تعديل مصدري - تعديل العلاقات البريطانية اللبنانية هي العلاقات الثنائية التي تجمع بين المملكة المتحدة ولبنان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومر�...

American baseball player (born 1990) Baseball player Tim HillHill with the San Diego Padres in 2022Chicago White Sox – No. 54PitcherBorn: (1990-02-10) February 10, 1990 (age 34)Mission Hills, California, U.S.Bats: RightThrows: LeftMLB debutMarch 29, 2018, for the Kansas City RoyalsMLB statistics (through April 14, 2024)Win–loss record16–14Earned run average4.23Strikeouts210 Teams Kansas City Royals (2018–2019) San Diego Padres (2020–2023) Chicago White Sox (2024�...

Voce principale: Vicenza Calcio. Associazione Fascista Calcio VicenzaStagione 1943-1944Sport calcio SquadraVicenza Calcio Allenatore Italo Ferrero poi Pietro Spinato Presidente Antonio Roi Divisione Nazionale 1943-19441º posto nel Campionato Veneto girone B. Maggiori presenzeCampionato: Colaussi, Suppi (11) Miglior marcatoreCampionato: Quaresima (9) 1942-1943 1945-1946 Si invita a seguire il modello di voce Questa voce raccoglie le informazioni riguardanti l'Associazione Fascista Calcio Vic...

Public university in Wrocław, Poland Leopoldina (university) redirects here. For the German National Academy of Sciences, see Leopoldina (academy of sciences). University of WrocławUniwersytet WrocławskiLatin: Universitas WratislaviensisFormer namesGerman: Leopoldina, Universität Breslau, Schlesische Friedrich-Wilhelms-Universität zu Breslau (before 1945)TypePublicEstablished21 October 1702; 321 years ago (1702-10-21) (reorganised 1945)PresidentRobert OlkiewiczAdministr...

В Википедии есть статьи о других людях с такой фамилией, см. Марков. Леонид Марков Имя при рождении Леонид Васильевич Марков Дата рождения 13 декабря 1927(1927-12-13)[1][2] Место рождения с. Алексеевка,Казахская АССР, СССР Дата смерти 1 марта 1991(1991-03-01)[3] (63 года) Место смер...

† Стеллерова корова Муляж стеллеровой коровы в Лондонском музее естествознания Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстно�...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: New Zealand cricket team in Sri Lanka in 2012–13 – news · newspapers · books · scholar · JSTOR (September 2012) (Learn how and when to remove this message) New Zealand cricket team in Sri Lanka in 2012–13 Sri Lanka New ZealandDates 30 October 2...
2020年夏季奥林匹克运动会波兰代表團波兰国旗IOC編碼POLNOC波蘭奧林匹克委員會網站olimpijski.pl(英文)(波兰文)2020年夏季奥林匹克运动会(東京)2021年7月23日至8月8日(受2019冠状病毒病疫情影响推迟,但仍保留原定名称)運動員206參賽項目24个大项旗手开幕式:帕维尔·科热尼奥夫斯基(游泳)和马娅·沃什乔夫斯卡(自行车)[1]闭幕式:卡罗利娜·纳亚(皮划艇)&#...

Penggilingan padi di Kota Baru, Uram Jaya, Lebong, Bengkulu Mesin penyemprot pestisida modern Alat dan mesin pertanian adalah berbagai alat dan mesin yang digunakan dalam usaha pertanian. Pengelompokan penggunaan istilah alat dan mesin pertanian tidak lepas dari definisi dari alat dan mesin itu sendiri. Perbedaan mendasar antara alat dan mesin adalah, mesin memiliki poros yang berputar, sedangkan alat tidak. Sehingga mesin bisa saja digerakkan dengan tenaga manusia. Lebih lengkapnya dapat dil...

لمعانٍ أخرى، طالع الحمة (توضيح).الحمّةالحمّةالقضاءطبرياالإحداثيات32°41′10″N 35°39′51″E / 32.68611°N 35.66417°E / 32.68611; 35.66417شبكة فلسطين212/232السكان336 (1948)المساحة1،692 دونم1،7 كم²تاريخ التهجير20 يوليو 1949سبب التهجيرطرد من قبل القوات الصهيونيةمستعمرات حاليةهامات غ�...

Nature preserve in California View from Arastradero Preserve, the Stanford Dish is in the background This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Arastradero Preserve – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message) Arastradero Preserve, officially ...

The ruling dynasty of Qatar House of Thaniآل ثانيParent houseBanu Hanzala[1]CountryQatarFoundedc. 1847FounderMohammed bin ThaniCurrent headTamim bin HamadTitles Hakim Emir Sheikh TraditionsIslam (Sunni) Politics of Qatar Member State of the Arab League Constitution Human rights Monarchy Emir Tamim bin Hamad Al Thani Cabinet Prime Minister Mohammed bin Abdulrahman Al Thani Consultative Assembly Consultative Assembly Chairman Ahmad bin Abdullah Al Mahmoud Elections Recent el...

Japanese urban legend of two-mouthed woman This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Futakuchi-onna – news · newspapers · books · scholar · JSTOR (April 2018) An image of futakuchi-onna from the Ehon Hyaku Monogatari Futakuchi-onna (ふたくちおんな, two-mouthed woman) is a type of yōka...
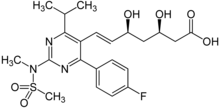
Regulatory class of pharmaceutical drug An orphan drug is a pharmaceutical agent that is developed to treat certain rare medical conditions. An orphan drug would not be profitable to produce without government assistance, due to the small population of patients affected by the conditions. The conditions that orphan drugs are used to treat are referred to as orphan diseases. The assignment of orphan status to a disease and to drugs developed to treat it is a matter of public policy that depend...

Book by Abdul Kalam This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (November 2011) (Learn how and when to remove this message) Ignited Minds This article is part of a series aboutA. P. J. Abdul Kalam President of India(2002-2007) Awards and honours Eponym World Students' Day Presidential election 2002 Books and ...

Australian politician This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Frank Bond politician – news · newspapers · books · scholar · JSTOR (May 2016) Frank Bond (1856 – 15 December 1931) was an Australian politician. He was born in Longford, Tasmania. In 1903 he was elected to the Tasmani...

「シェイク」はこの項目へ転送されています。その他の用法については「シェイク (曖昧さ回避)」をご覧ください。 イスラム教 教義・信仰 アッラーフ · イスラーム 六信 · 五行 タウヒード · ジハード モスク · マドラサ カアバ · ハッジ 指導者 ムハンマド ハディージャ · アーイシャ アブー・バクル ウ�...

Questa voce sull'argomento algebra è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Questa voce o sezione sull'argomento matematica non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Il lemma della farfalla è un risultato utilizzato nell'algebra. Siano U {\displaystyl...

Map of arrondissements of the Ardèche department. The 3 arrondissements of the Ardèche department are:[1] Arrondissement of Largentière, (subprefecture: Largentière) with 151 communes.[2] The population of the arrondissement was 101,490 in 2016. Arrondissement of Privas, (prefecture of the Ardèche department: Privas) with 66 communes. The population of the arrondissement was 84,907 in 2016. Arrondissement of Tournon-sur-Rhône, (subprefecture: Tournon-sur-Rhône) with 118...

For the cycling team, see Adria Mobil (cycling team). Adria Mobil motorhome as sponsor of 2021 Tour of Slovenia Adria Adora 572 UT Adria Mobil is a Slovene speciality vehicle manufacturer company based in Novo Mesto that specializes in production of travel trailers and recreational vehicles. The company's products are branded under under the Adria brand name, and it markets and sells its entire stock within the European single market.[1] Adria motorhomes are commonly based on Fiat and...



















![{\displaystyle [G:H]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28c19ed6f18e6db133b5a0257ecde8026808fd1c)

