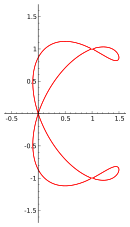
Плоская кривая четвёртой степени
|
Read other articles:

Love in SpacePoster di film Love in SpaceSutradaraTony ChanWing ShyaProduserFruit ChanSkenarioTony ChanHo Man ManPemeranAaron KwokEason ChanRené LiuKwai Lun-MeiAngelababy YeungJing BoranXu FanSinematograferBartek KaczmarekPerusahaanproduksiSundream Motion PicturesHuayi Brothers Media GroupFox International ProductionsDistributorSundream Motion PicturesHuayi Brothers20th Century FoxTanggal rilis8 September 2011Negara Hong KongBahasaMandarinKantonisInggris Love in Space (Hanzi sederhana: �...

Pertempuran Kambula Pertempuran Kambula terjadi pada tahun 1879 selama masa perang Inggris-Zulu (perang Anglo-Zulu). Hal ini terjadi ketika pasukan tentara Zulu menyerang perkemahan tentara Inggris di Kambula, pertempuran ini dimenangkan oleh Inggris dan menjadi awal dari perang Anglo-Zulu. Pranala luar Natal Native Horseman at Kambula Diarsipkan 2011-05-26 di Wayback Machine. battle-of-khambula Travellers Impressions Diarsipkan 2007-10-20 di Wayback Machine. Anglo-Zulu War: Battle of Khambul...

Argentine football manager Miguel Ángel Zahzú Zahzú in 2007Personal informationFull name Miguel Ángel ZahzúDate of birth (1966-02-24) 24 February 1966 (age 58)Place of birth Morón, ArgentinaHeight 1.87 m (6 ft 2 in)Position(s) GoalkeeperYouth career Vélez SarsfieldSenior career*Years Team Apps (Gls)1987–1988 Atlético Lugano 1988–1989 Midland 38 (0)1989–1990 San Telmo 1990–1991 Nueva Chicago 1991–1993 Laferrere 1994 Cobreloa 1994–1995 Colegiales 1995 Arg...

L'expression de monde arabe (arabe : العالم العربي, al-ʿālam al-ʿarabī ou الوطن العربي al-wațan al-ʿarabī) désigne un ensemble de pays couvrant la péninsule arabique, l'Afrique du Nord et le Proche-Orient, ayant en commun la langue arabe. Bien qu'assez largement utilisé, ce terme ne renvoie pas à une liste définie de pays, et à la différence de la Ligue arabe par exemple, le monde arabe ne constitue pas une entité politique formelle. On peut néanmoi...

رجاء لا تعدل هذه الصفحة هنا لأنها نسخة عن صفحة في الميتا. يمكنك تعديل الصفحة هناك. صفحة التفضيلات تتيح لك تخصيص بعض جوانب برنامج ميدياويكي الذي يقوم بتشغيل ويكيبيديا وباقي المشاريع الشقيقة الأخرى ، وهي متاحة فقط عندما تقوم بتسجيل الدخول. لتعديل تفضيلاتك قم بالنقر على رابط �...

Air warfare branch of Libya's armed forces For the air force of Libya's National Transitional Council, see Free Libyan Air Force. Libyan Air Forceالقوات الجوية الليبيةLibyan Air Force emblemActive1962; 62 years ago (1962)Country LibyaAllegianceGovernment of National UnityHouse of Representatives FormerlyGovernment of National AccordBranchLibyan Armed ForcesTypeAir forceRoleAerial warfareSize4,500 personnelHeadquartersTripoli (GNU-backed)Tobruk (HoR-ba...

Species of bird White-naped crane White-naped crane at Saijo, Ehime, Japan Conservation status Vulnerable (IUCN 3.1)[1] CITES Appendix I (CITES)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Order: Gruiformes Family: Gruidae Genus: Antigone Species: A. vipio Binomial name Antigone vipio(Pallas, 1811) Geographical distribution. Green: Breeding Yellow: Migratory passage Red: Non-breeding The white-naped crane (Antig...

烏克蘭總理Прем'єр-міністр України烏克蘭國徽現任杰尼斯·什米加尔自2020年3月4日任命者烏克蘭總統任期總統任命首任維托爾德·福金设立1991年11月后继职位無网站www.kmu.gov.ua/control/en/(英文) 乌克兰 乌克兰政府与政治系列条目 宪法 政府 总统 弗拉基米尔·泽连斯基 總統辦公室 国家安全与国防事务委员会 总统代表(英语:Representatives of the President of Ukraine) 总...

Questa voce sull'argomento calciatori francesi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Jean-Marc Pilorget Nazionalità Francia Altezza 180 cm Peso 74 kg Calcio Ruolo Allenatore (ex difensore) Termine carriera 1990 - giocatore CarrieraSquadre di club1 1975-1987 Paris Saint-Germain336 (12)1987-1988 Cannes29 (1)1988-1989 Paris Saint-Germain35 (2)1989-1990 Guingamp25 (0)Ca...

1997–98 World CupWinnersOverall Primož PeterkaSki Jumping (NH, LH) Primož PeterkaSki Flying Sven HannawaldFour Hills Tournament Kazuyoshi FunakiNordic Tournament Andreas WidhölzlNations Cup JapanCompetitionsVenues20Individual27Cancelled1← 1996–97 1998–99 → The 1997–98 FIS Ski Jumping World Cup was the 19th World Cup season in ski jumping and the 8th official World Cup season in ski flying. It began in Lillehammer, Norway on 29 November 1997 and finished i...

US security policy think tank For the think tank based in Geneva, Switzerland, see Geneva Centre for Security Policy. Center for Security PolicyAbbreviationCSPFormation1988 (36 years ago) (1988)FounderFrank J. Gaffney, Jr.[1][2]TypenonprofitTax ID no. 52-1601976Legal status501(c)(3)[3]Purposedefense policy think tankHeadquarters PMB 189 2020 Pennsylvania Avenue, NW Washington, D.C. 20006-1811 United States PresidentTommy Waller[a]ChairmanE. Miles ...

Seafood from the Cantabrian Sea This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Cantabrian cuisine – news · newspapers · books · scholar · JSTOR (August 2015) The cocido montañés, the most representative dish of Cantabrian cuisine. Cantabrian cuisine is the cuisine from Cantabria, an autonomous c...

Acropoli di AlatriCivitaAcropoli di Alatri. La Porta MaggioreLocalizzazioneStato Italia Altitudine502 m s.l.m. DimensioniSuperficie19 000 m² Mappa di localizzazione Modifica dati su Wikidata · Manuale L'Acropoli di Alatri, nota localmente come Civita, è posta nel cuore del centro storico di Alatri, sulla cima del colle su cui sorge la città, a circa 500 m s.l.m. La rocca è cinta da mura in opera poligonale, dette mura ciclopiche; vi si accede da due porte (P...

Jalaratan lima jalur di NY 78 di Amherst, New York, dikelilingi oleh pengembangan komersial berorientasi mobil dengan trotoar kosong Jalaratan (lakuran dari jalan + ratan ) adalah jenis jalantama yang merupakan perpaduan antara ratan dan jalan. [1] [2] Umum di Amerika Serikat dan Kanada, jalaratan adalah arteri lebar yang sering kali menyediakan akses ke mal, drive-through, dan bisnis berorientasi mobil lainnya. [3] Para perencana kota mengkritik jalaratan tersebut kar...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (نوفمبر 2023) موسيقى جامايكا تضم الموسيقى الشعبية الجامايكية والعديد من الأنماط الموسي...

TubelightPoster rilis layar lebarNama lainHindiट्यूब लाइट SutradaraKabir KhanProduserSalman KhanKabir KhanDitulis olehKabir KhanSkenario Kabir Khan Parveez Sheikh CeritaKabir KhanBerdasarkanLittle Boyoleh Alejandro Gómez Monteverde[1][2][3]PemeranSalman KhanSohail KhanOm PuriMatin Rey TanguZhu Zhu Shah Rukh KhanPenata musikPritam(lagu)Julius Packiam(musik latarSinematograferAseem MishraPenyuntingRameshwar S. BhagatPerusahaanproduksiSalman...

2 Tawarikh 24Kitab Tawarikh (Kitab 1 & 2 Tawarikh) lengkap pada Kodeks Leningrad, dibuat tahun 1008.KitabKitab 2 TawarikhKategoriKetuvimBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen14← pasal 23 pasal 25 → 2 Tawarikh 24 (atau II Tawarikh 24, disingkat 2Taw 24) adalah pasal kedua puluh empat Kitab 2 Tawarikh dalam Alkitab Ibrani dan Perjanjian Lama di Alkitab Kristen. Dalam Alkitab Ibrani termasuk dalam bagian Ketuvim (כְּתוּבִים, tulisan).[1] ...
American business executive (born 1960) For other people named Tim Cook, see Tim Cook (disambiguation). Tim CookCook in 2023BornTimothy Donald Cook (1960-11-01) November 1, 1960 (age 63)Mobile, Alabama, U.S.EducationAuburn University (BS)Duke University (MBA)TitleCEO of Apple Inc. (2011–present)WebsiteApple Leadership ProfileSignature Timothy Donald Cook (born November 1, 1960)[1] is an American business executive who is the current chief executive officer of Apple Inc. Cook ha...

La liste des députés d'Eure-et-Loir recense par ordre chronologique, depuis la Révolution française, les députés élus par le département d'Eure-et-Loir à l'Assemblée nationale . Révolution française (1789-1799) Jérôme Pétion de Villeneuve, salle du serment du Jeu de paume - Versailles. Claude-Adrien Jumentier. Antoine Omer Talon. États généraux et Assemblée constituante (1789-1791) Le département d'Eure-et-Loir n'ayant été créé que le 4 mars 1790, les représentants au...

New Zealand-born actor (1917–1985) Ewen Solonas Lucas in TV's Maigret (1960-1963)BornPeter Ewen Solon(1917-09-07)7 September 1917Auckland, New ZealandDied7 July 1985(1985-07-07) (aged 67)Addlestone, Surrey, EnglandOccupationActor Peter Ewen Solon (7 September 1917 – 7 July 1985)[1] was a New Zealand-born actor, who worked extensively in both the United Kingdom and Australia.[2][3] At the outbreak of World War II, Solon became a member of the First Echelon, 2nd...