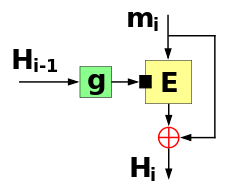
Односторонняя функция сжатия
|
Read other articles:

Painting by Jean-Honoré Fragonard The Storm (c. 1759) by Jean-Honoré Fragonard The Storm (French: L'Orage) (also known as The Stalled Cart or Wagon in the Mud French: La Charrette embourbée)[1][2] is an oil on canvas painting by Jean-Honoré Fragonard that hangs in the Louvre. Painted during his time in Rome, it was inspired by the caravan pictures of Giovanni Benedetto Castiglione that were particularly admired in Paris.[3] The painting, 0.73m high and 0.97m wide, ...

В Википедии есть статьи о других людях с фамилией Семёнов-Тян-Шанский. В Википедии есть статьи о других людях с такими же именем и фамилией: Семёнов, Пётр. Пётр Петрович Семёнов-Тян-Шанский П. П. Семёнов-Тян-Шанский (1870-е годы) Дата рождения 2 (14) января 1827[1] Место рождения...

American reconnaissance satellite launched in 1959; failed to achieve orbit Discoverer 1An Agena-A stage [1]Mission typeTechnologyOperatorU.S. Air Force / CIAHarvard designation1959 Beta 1COSPAR ID1959-002A SATCAT no.00013Mission duration17 days Spacecraft propertiesSpacecraftDiscovererSpacecraft typeCORONA Test VehicleBusAgena-AManufacturerDouglas Aircraft CompanyLaunch mass618 kgDimensions5.73 m long1.52 m diameter Start of missionLaunch date28 February 1959,21:49:16 GMTRocketThor-A...

Amphibious warfare vessel USS Balduck (APD-132) on 23 March 1954 History United States NameUSS Balduck NamesakeRemi A. Balduck BuilderDefoe Shipbuilding Company, Bay City, Michigan Laid down17 June 1944 Launched27 October 1944 Commissioned7 May 1945 Decommissioned31 May 1946 Recommissioned5 November 1953 Decommissioned28 February 1958 ReclassifiedLPR-132, 1 January 1969 Stricken15 July 1975 FateSold for scrap, 1 December 1976 General characteristics Class and typeCrosley-class high speed tran...

باليامبيلا تقسيم إداري البلد اليونان [1] إحداثيات 38°54′39″N 20°57′06″E / 38.91075°N 20.95178°E / 38.91075; 20.95178 السكان التعداد السكاني 514 (resident population of Greece) (2021)992 (resident population of Greece) (2001)1000 (resident population of Greece) (1991)762 (resident population of Greece) (2011) الرمز الجغرافي 256036 تعديل مصدري ...

Robert FiskRobert Fisk di Al Jazeera Forum 2010Lahir(1946-07-12)12 Juli 1946Maidstone, Kent, InggrisMeninggal30 Oktober 2020(2020-10-30) (umur 74)Dublin, IrlandiaWarga negara Irlandia Inggris Pendidikan Universitas Lancaster (BA, 1968) Trinity College Dublin (PhD, 1985) PekerjaanKoresponden Timur Tengah untuk The IndependentKarya terkenal Jacob's Award Amnesty International UK Press Awards British Press Awards International Journalist of the Year Lannan Cultural Freedom Prize Suami/istr...

Former currency of San Marino Sammarinese liralira sanmarinese (Italian) 500 LireISO 4217CodeITL (abbreviation SML is used)UnitUnitliraPlurallireSymbolL. (None official, see Italian lira)DenominationsSubunit 1⁄100centesimoSubunits were abolished after WWIIPlural centesimocentesimi (c.)BanknotesItalian lira banknotesCoins Freq. used50, 100, 200, 500, 1,000 Lire Rarely used1 Lira, 2, 5, 10, 20 LireDemographicsUser(s)None, previously: Ital...

UFC mixed martial arts event in 2014 UFC Fight Night: Brown vs. SilvaThe poster for UFC Fight Night: Brown vs. SilvaInformationPromotionUltimate Fighting ChampionshipDateMay 10, 2014 (2014-05-10)VenueU.S. Bank ArenaCityCincinnati, OhioAttendance6,143[1]Total gate$415,000[1]Event chronology UFC 172: Jones vs. Teixeira UFC Fight Night: Brown vs. Silva UFC 173: Barao vs. Dillashaw UFC Fight Night: Brown vs. Silva (also known as UFC Fight Night 40) was a mixed marti...

Kate BruceBruce di 1921Lahir(1860-02-17)17 Februari 1860Columbus, Indiana, A.S.Meninggal2 April 1946(1946-04-02) (umur 86)New York, New York, A.S.PekerjaanAktrisTahun aktif1908-1931 Kate Bruce (17 Februari 1860 – 2 April 1946) adalah seorang aktris Amerika dari era film bisu.[1] Dia muncul di 289 film antara 1908 dan 1931. Dia lahir di Columbus, Indiana, dan meninggal di New York, New York. Pada tahun 1885, Bruce meninggalkan Boone, Iowa, dalam sebuah geroba...

Sumber referensi dari artikel ini belum dipastikan dan mungkin isinya tidak benar. Mohon periksa, kembangkan artikel ini, dan tambahkan sumber yang benar pada bagian yang diperlukan. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Endemol GroupIndustriProduksiDistribusiLisensiMediaGenrePerusahaan produksiNasibBergabung dengan Shine Group dan membentuk Endemol Shine Group, kemudian berubah nama menjadi BanijayPenerusBanijayDidirikan1994PendiriJoop van den EndeJohn de MolDit...

Dangé-Saint-Romaincomune Dangé-Saint-Romain – Veduta LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Vienne ArrondissementChâtellerault CantoneChâtellerault-2 TerritorioCoordinate46°56′14″N 0°36′24″E / 46.937222°N 0.606667°E46.937222; 0.606667 (Dangé-Saint-Romain)Coordinate: 46°56′14″N 0°36′24″E / 46.937222°N 0.606667°E46.937222; 0.606667 (Dangé-Saint-Romain) Altitudine37-127 m s.l.m....

Gerry O'Hara Nazionalità Inghilterra Calcio Ruolo Centrocampista Termine carriera 1982 CarrieraGiovanili 19??-1975 WolverhamptonSquadre di club1 1975-1978 Wolverhampton9 (0)1978-1979 Hereford Utd1 (0)1979-1982 Worcester City41 (11) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Gerald John O'Hara, più conosciuto con il dimi...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) حققت الامبراطورية العثمانية خلال 600 سنة في فترة حكمها تقدما كبيرا في العلوم والتكنولوجيا على نطاق واسع ف�...

Historic district in Maryland, United States United States historic placeCatoctin Furnace Historic DistrictU.S. National Register of Historic PlacesU.S. Historic district Show map of MarylandShow map of the United StatesLocationCatoctin Furnace, MarylandCoordinates39°34′35″N 77°26′2″W / 39.57639°N 77.43389°W / 39.57639; -77.43389Built1774NRHP reference No.72000578Added to NRHPFebruary 11, 1972[1] Catoctin Furnace (also known as Catoctin Ir...

Commuter rail station in Highwood, Illinois Fort SheridanFort Sheridan station in October 2015.General informationLocation461 West Old Elm RoadFort Sheridan, IllinoisCoordinates42°13′03″N 87°49′16″W / 42.2174°N 87.8210°W / 42.2174; -87.8210Owned byMetraPlatforms2 Side platformsTracks2 tracksConnections Pace BusesConstructionParkingYesAccessibleYesOther informationFare zone4Passengers2018259 (average weekday)[1] 5.5%Rank156 out of 23...

1955 film by Nicholas Ray Run for CoverTheatrical release posterDirected byNicholas RayScreenplay byWinston MillerStory byHarriet Frank, Jr.Irving RavetchProduced byWilliam H. PineWilliam C. ThomasStarringJames CagneyViveca LindforsJohn DerekCinematographyDaniel FappEdited byHoward SmithMusic byHoward JacksonColor processTechnicolorProductioncompanyPine-Thomas ProductionsDistributed byParamount PicturesRelease date May 14, 1955 (1955-05-14) (United States) Running time93 mi...

Politics of the Philippines Government Constitution of the Philippines Charter Change Laws Legal codes Taxation Executive President of the Philippines Bongbong Marcos (PFP) Vice President of the Philippines Sara Duterte (HNP) Cabinet (lists) Executive departments Local government Legislature Congress of the Philippines 19th Congress Senate President Migz Zubiri (Independent) House of Representatives Speaker Martin Romualdez (Lakas) Districts Party-list representation Bangsamoro Parliament Pro...

Pertemuan komunitas adalah cara yang digunakan FEMA dan SBA untuk mendistribusikan informasi setelah bencana. Badan musyawarah adalah sebuah organisasi yang secara bersama membuat keputusan setelah debat dan diskusi. Contoh dari badan musyawarah termasuk legislatif, dewan direksi, badan administratif dan rapat anggota dari sebuah serikat, klub atau organisasi lainnya. Biasanya keputusan oleh badan ini dibuat atas dasar pemungutan suara, debat dan amendemen, dilakukan sesuai dengan kebiasaan a...

Pour les articles homonymes, voir Benitez. Cet article est une ébauche concernant un footballeur paraguayen. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Miguel Ángel Benítez Biographie Nationalité Paraguayen Naissance 19 mai 1970 (54 ans) Asuncion Taille 1,71 m (5′ 7″) Poste Attaquant Parcours senior1 SaisonsClubsM (B.)1993-1995 CA de Madrid10 (0)1994-1995 Mérida UD23 (...

Conflicts mainly between the Kingdom of Mysore and the British East India Company (late 1700s) Part of a series on the Wars of Great Britain Other wars War of the Quadruple Alliance Jacobite risings Anglo-Mysore Wars First Anglo-Maratha War American Revolutionary War Fourth Anglo-Dutch War Australian frontier wars Hawkesbury and Nepean Wars American Indian Wars Queen Anne's War Dummer's War King George's War War of Jenkins' Ear French and Indian War Father Le Loutre's War Second Hundred Years...