–Я–∞—А–∞–і–ЊћБ–Ї—Б –і–љ–µ–є —А–Њ–ґ–і–µћБ–љ–Є—П вАФ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ, —Б–Њ—Б—В–Њ—П—Й–µ–µ –≤ —В–Њ–Љ, —З—В–Њ –≤ –≥—А—Г–њ–њ–µ, —Б–Њ—Б—В–Њ—П—Й–µ–є –Є–Ј 23 –Є–ї–Є –±–Њ–ї–µ–µ —З–µ–ї–Њ–≤–µ–Ї, –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П (—З–Є—Б–ї–Њ –Є –Љ–µ—Б—П—Ж) —Е–Њ—В—П –±—Л —Г –і–≤—Г—Е –ї—О–і–µ–є –њ—А–µ–≤—Л—И–∞–µ—В 50 % . –Э–∞–њ—А–Є–Љ–µ—А, –µ—Б–ї–Є –≤ –Ї–ї–∞—Б—Б–µ 23 —Г—З–µ–љ–Є–Ї–∞ –Є–ї–Є –±–Њ–ї–µ–µ, —В–Њ –±–Њ–ї–µ–µ –≤–µ—А–Њ—П—В–љ–Њ —В–Њ, —З—В–Њ —Г –Ї–∞–Ї–Њ–є-—В–Њ –њ–∞—А—Л –Њ–і–љ–Њ–Ї–ї–∞—Б—Б–љ–Є–Ї–Њ–≤ –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П –њ—А–Є–і—Г—В—Б—П –љ–∞ –Њ–і–Є–љ –і–µ–љ—М, —З–µ–Љ —В–Њ, —З—В–Њ —Г –Ї–∞–ґ–і–Њ–≥–Њ –±—Г–і–µ—В —Б–≤–Њ–є –љ–µ–њ–Њ–≤—В–Њ—А–Є–Љ—Л–є –і–µ–љ—М —А–Њ–ґ–і–µ–љ–Є—П [ 1] –†–Є—Е–∞—А–і–Њ–Љ –Ь–Є–Ј–µ—Б–Њ–Љ –≤ 1939 –≥–Њ–і—Г[ 2] [ 3]
–Ф–ї—П 57 –Є –±–Њ–ї–µ–µ —З–µ–ї–Њ–≤–µ–Ї –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–∞–Ї–Њ–≥–Њ —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –њ—А–µ–≤—Л—И–∞–µ—В 99 % , —Е–Њ—В—П 100 % –Њ–љ–∞ –і–Њ—Б—В–Є–≥–∞–µ—В, —Б–Њ–≥–ї–∞—Б–љ–Њ –њ—А–Є–љ—Ж–Є–њ—Г –Ф–Є—А–Є—Е–ї–µ , —В–Њ–ї—М–Ї–Њ —В–Њ–≥–і–∞, –Ї–Њ–≥–і–∞ –≤ –≥—А—Г–њ–њ–µ –љ–µ –Љ–µ–љ–µ–µ 367 —З–µ–ї–Њ–≤–µ–Ї (—А–Њ–≤–љ–Њ –љ–∞ 1 –±–Њ–ї—М—И–µ, —З–µ–Љ —З–Є—Б–ї–Њ –і–љ–µ–є –≤ –≤–Є—Б–Њ–Ї–Њ—Б–љ–Њ–Љ –≥–Њ–і—Г; —Б —Г—З—С—В–Њ–Љ –≤–Є—Б–Њ–Ї–Њ—Б–љ—Л—Е –ї–µ—В).
–Ґ–∞–Ї–Њ–µ —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –Љ–Њ–ґ–µ—В –њ–Њ–Ї–∞–Ј–∞—В—М—Б—П –љ–µ–Њ—З–µ–≤–Є–і–љ—Л–Љ, —В–∞–Ї –Ї–∞–Ї –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П –і–≤—Г—Е —З–µ–ї–Њ–≤–µ–Ї —Б –ї—О–±—Л–Љ –і–љ—С–Љ –≤ –≥–Њ–і—Г
(
1
365
=
0
,
27
% % -->
)
{\displaystyle ({\tfrac {1}{365}}=0{,}27\,\%)}
1
365
× √Ч -->
23
=
6
,
3
% % -->
{\displaystyle {\tfrac {1}{365}}\times 23=6{,}3\,\%}
—З–Є—Б–ї–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –њ–∞—А
(
23
× √Ч -->
22
2
=
253
)
{\displaystyle ({\tfrac {23\times 22}{2}}=253)}
253 > 23 ). –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, —Г—В–≤–µ—А–ґ–і–µ–љ–Є–µ –љ–µ —П–≤–ї—П–µ—В—Б—П –њ–∞—А–∞–і–Њ–Ї—Б–Њ–Љ –≤ —Б—В—А–Њ–≥–Њ–Љ –љ–∞—Г—З–љ–Њ–Љ —Б–Љ—Л—Б–ї–µ: –ї–Њ–≥–Є—З–µ—Б–Ї–Њ–≥–Њ –њ—А–Њ—В–Є–≤–Њ—А–µ—З–Є—П –≤ –љ—С–Љ –љ–µ—В, –∞ –њ–∞—А–∞–і–Њ–Ї—Б –Ј–∞–Ї–ї—О—З–∞–µ—В—Б—П –ї–Є—И—М –≤ —А–∞–Ј–ї–Є—З–Є—П—Е –Љ–µ–ґ–і—Г –Є–љ—В—Г–Є—В–Є–≤–љ—Л–Љ –≤–Њ—Б–њ—А–Є—П—В–Є–µ–Љ —Б–Є—В—Г–∞—Ж–Є–Є —З–µ–ї–Њ–≤–µ–Ї–Њ–Љ –Є —А–µ–Ј—Г–ї—М—В–∞—В–∞–Љ–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞—Б—З—С—В–∞.
–У—А–∞—Д–Є–Ї –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П —Е–Њ—В—П –±—Л —Г –і–≤—Г—Е —З–µ–ї–Њ–≤–µ–Ї –Њ—В –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ –ї—О–і–µ–є
–Т –≥—А—Г–њ–њ–µ –Є–Ј 23 —З–µ–ї–Њ–≤–µ–Ї –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П —Г –і–≤—Г—Е —З–µ–ї–Њ–≤–µ–Ї —Б—В–Њ–ї—М –≤—Л—Б–Њ–Ї–∞, –њ–Њ—В–Њ–Љ—Г —З—В–Њ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ—В—Б—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П —Г –ї—О–±—Л—Е –і–≤—Г—Е —З–µ–ї–Њ–≤–µ–Ї –≤ –≥—А—Г–њ–њ–µ. –≠—В–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ–Љ –њ–∞—А –ї—О–і–µ–є, –Ї–Њ—В–Њ—А—Л–µ –Љ–Њ–ґ–љ–Њ —Б–Њ—Б—В–∞–≤–Є—В—М –Є–Ј 23 —З–µ–ї–Њ–≤–µ–Ї. –Ґ–∞–Ї –Ї–∞–Ї –њ–Њ—А—П–і–Њ–Ї –ї—О–і–µ–є –≤ –њ–∞—А–∞—Е –љ–µ –Є–Љ–µ–µ—В –Ј–љ–∞—З–µ–љ–Є—П, –Њ–±—Й–µ–µ —З–Є—Б–ї–Њ —В–∞–Ї–Є—Е –њ–∞—А —А–∞–≤–љ–Њ —З–Є—Б–ї—Г —Б–Њ—З–µ—В–∞–љ–Є–є –Є–Ј 23 –њ–Њ 2, —В–Њ –µ—Б—В—М (23 √Ч 22) / 2 = 253 –њ–∞—А—Л .
–Т —Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–Ї–µ –њ–∞—А–∞–і–Њ–Ї—Б–∞ —А–µ—З—М –Є–і—С—В –Є–Љ–µ–љ–љ–Њ –Њ —Б–Њ–≤–њ–∞–і–µ–љ–Є–Є –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П —Г –Ї–∞–Ї–Є—Е-–ї–Є–±–Њ –і–≤—Г—Е —З–ї–µ–љ–Њ–≤ –≥—А—Г–њ–њ—Л. –Ю–і–љ–Њ –Є–Ј —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ—С–љ–љ—Л—Е –Ј–∞–±–ї—Г–ґ–і–µ–љ–Є–є —Б–Њ—Б—В–Њ–Є—В –≤ —В–Њ–Љ, —З—В–Њ —Н—В–Њ—В —Б–ї—Г—З–∞–є –њ—Г—В–∞—О—В —Б –і—А—Г–≥–Є–Љ —Б–ї—Г—З–∞–µ–Љ, –љ–∞ –њ–µ—А–≤—Л–є –≤–Ј–≥–ї—П–і –њ–Њ—Е–Њ–ґ–Є–Љ, –Ї–Њ–≥–і–∞ –Є–Ј –≥—А—Г–њ–њ—Л –≤—Л–±–Є—А–∞–µ—В—Б—П –Њ–і–Є–љ —З–µ–ї–Њ–≤–µ–Ї –Є –Њ—Ж–µ–љ–Є–≤–∞–µ—В—Б—П –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ –і–µ–љ—М —А–Њ–ґ–і–µ–љ–Є—П –Ї–∞–Ї–Є—Е-–ї–Є–±–Њ –і—А—Г–≥–Є—Е —З–ї–µ–љ–Њ–≤ –≥—А—Г–њ–њ—Л —Б–Њ–≤–њ–∞–і—С—В —Б –і–љ—С–Љ —А–Њ–ґ–і–µ–љ–Є—П –≤—Л–±—А–∞–љ–љ–Њ–≥–Њ —З–µ–ї–Њ–≤–µ–Ї–∞. –Т –њ–Њ—Б–ї–µ–і–љ–µ–Љ —Б–ї—Г—З–∞–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ –љ–Є–ґ–µ.
–Ґ—А–µ–±—Г–µ—В—Б—П –Њ–њ—А–µ–і–µ–ї–Є—В—М –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ –≤ –≥—А—Г–њ–њ–µ –Є–Ј n —З–µ–ї–Њ–≤–µ–Ї –Ї–∞–Ї –Љ–Є–љ–Є–Љ—Г–Љ —Г –і–≤—Г—Е –Є–Ј –љ–Є—Е –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П —Б–Њ–≤–њ–∞–і—Г—В.
–Я—Г—Б—В—М –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ , —В–Њ –µ—Б—В—М –њ—А–Є–Љ–µ–Љ, —З—В–Њ:
–Т –і–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В–Є —Н—В–Њ –љ–µ —Б–Њ–≤—Б–µ–Љ —В–∞–Ї вАФ –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –≤ –љ–µ–Ї–Њ—В–Њ—А—Л—Е —Б—В—А–∞–љ–∞—Е –Є–Ј-–Ј–∞ –Њ—Б–Њ–±–µ–љ–љ–Њ—Б—В–µ–є —А–∞–±–Њ—В—Л –±–Њ–ї—М–љ–Є—Ж –±–Њ–ї—М—И–µ –і–µ—В–µ–є —А–Њ–ґ–і–∞–µ—В—Б—П –≤ –Њ–њ—А–µ–і–µ–ї—С–љ–љ—Л–µ –і–љ–Є –љ–µ–і–µ–ї–Є. –Ю–і–љ–∞–Ї–Њ –љ–µ—А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ—Б—В—М —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є—П –Љ–Њ–ґ–µ—В –ї–Є—И—М —Г–≤–µ–ї–Є—З–Є—В—М –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П, –љ–Њ –љ–µ —Г–Љ–µ–љ—М—И–Є—В—М: –µ—Б–ї–Є –±—Л –≤—Б–µ –ї—О–і–Є —А–Њ–ґ–і–∞–ї–Є—Б—М —В–Њ–ї—М–Ї–Њ –≤ 3 –і–љ—П –Є–Ј 365, —В–Њ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П –±—Л–ї–∞ –±—Л –Њ—З–µ–љ—М –≤—Л—Б–Њ–Ї–Њ–є.
–†–∞—Б—Б—З–Є—В–∞–µ–Љ —Б–љ–∞—З–∞–ї–∞
p
¯ ¬ѓ -->
(
n
)
{\displaystyle {\bar {p}}(n)}
n
{\displaystyle n}
n
>
365
{\displaystyle n>365}
–њ—А–Є–љ—Ж–Є–њ–∞ –Ф–Є—А–Є—Е–ї–µ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М
p
¯ ¬ѓ -->
(
n
)
{\displaystyle {\bar {p}}(n)}
n
⩽ в©љ -->
365
{\displaystyle n\leqslant 365}
1
− вИТ -->
1
365
{\displaystyle 1-{\frac {1}{365}}}
1
− вИТ -->
2
365
{\displaystyle 1-{\frac {2}{365}}}
1
− вИТ -->
n
− вИТ -->
1
365
{\displaystyle 1-{\frac {n-1}{365}}}
p
¯ ¬ѓ -->
(
n
)
=
{\displaystyle {\bar {p}}(n)=}
1
⋅ вЛЕ -->
(
1
− вИТ -->
1
365
)
⋅ вЛЕ -->
(
1
− вИТ -->
2
365
)
⋅ вЛЕ -->
… вА¶ -->
⋅ вЛЕ -->
(
1
− вИТ -->
n
− вИТ -->
1
365
)
=
{\displaystyle 1\cdot \left(1-{\frac {1}{365}}\right)\cdot \left(1-{\frac {2}{365}}\right)\cdot \ldots \cdot \left(1-{\frac {n-1}{365}}\right)=}
365
⋅ вЛЕ -->
364
⋅ вЛЕ -->
… вА¶ -->
⋅ вЛЕ -->
(
365
− вИТ -->
n
+
1
)
365
n
=
{\displaystyle {365\cdot 364\cdot \ldots \cdot (365-n+1) \over 365^{n}}=}
365
!
365
n
(
365
− вИТ -->
n
)
!
.
{\displaystyle {365! \over 365^{n}(365-n)!}.}
–Ґ–Њ–≥–і–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ —Е–Њ—В—П –±—Л —Г –і–≤—Г—Е —З–µ–ї–Њ–≤–µ–Ї –Є–Ј n –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П —Б–Њ–≤–њ–∞–і—Г—В, —А–∞–≤–љ–∞
p
(
n
)
=
1
− вИТ -->
p
¯ ¬ѓ -->
(
n
)
.
{\displaystyle p(n)=1-{\bar {p}}(n).}
–Ч–љ–∞—З–µ–љ–Є–µ —Н—В–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –њ—А–µ–≤–Њ—Б—Е–Њ–і–Є—В 1/2 –њ—А–Є
n
=
23
{\displaystyle n=23}
p
(
22
)
≈ вЙИ -->
47
,
57
% % -->
{\displaystyle p(22)\approx 47,57\%}
n –Є —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є—Е –Є–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В–µ–є –њ—А–Є–≤–µ–і—С–љ –≤ —Б–ї–µ–і—Г—О—Й–µ–є —В–∞–±–ї–Є—Ж–µ.
n p (n )
10
12 %
20
41 %
30
70 %
50
97 %
100
99,99996 %
200
99,9999999999999999999999999998 %
300
(1 вИТ 7√Ч10вИТ73 ) √Ч 100 %
350
(1 вИТ 3√Ч10вИТ131 ) √Ч 100 %
367
100 %
–Ф–∞–љ–љ—Г—О –Ј–∞–і–∞—З—Г –Љ–Њ–ґ–љ–Њ –њ–µ—А–µ—Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞—В—М –≤ —В–µ—А–Љ–Є–љ–∞—Е –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–є ¬Ђ–Ј–∞–і–∞—З–Є –Њ —Б–Њ–≤–њ–∞–і–µ–љ–Є—П—Е¬ї. –Я—Г—Б—В—М:
—Г—А–љ–∞ —Б–Њ–і–µ—А–ґ–Є—В
M
{\displaystyle M}
M
{\displaystyle M}
—И–∞—А—Л –њ—А–Њ–љ—Г–Љ–µ—А–Њ–≤–∞–љ–љ—Л—Е —З–Є—Б–ї–∞–Љ–Є 1, 2, вА¶,
M
{\displaystyle M}
–њ—А–Њ–Є–Ј–≤–Њ–і–Є—В—Б—П –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ –≤—Л–±–Њ—А–Њ–Ї –њ–Њ n —И–∞—А–Њ–≤ –Є–Ј —Г—А–љ—Л (–≤ –і–∞–љ–љ–Њ–Љ —Б–ї—Г—З–∞–µ n вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —З–µ–ї–Њ–≤–µ–Ї –≤ –≥—А—Г–њ–њ–µ);
–Є–Ј—К—П—В—Л–µ —И–∞—А—Л –≤–Њ–Ј–≤—А–∞—Й–∞—О—В—Б—П –≤ —Г—А–љ—Г –њ–Њ—Б–ї–µ –Ї–∞–ґ–і–Њ–є –≤—Л–±–Њ—А–Ї–Є;
–≤—Л–±–Њ—А–Ї–Є —Б—З–Є—В–∞—О—В—Б—П —Г–њ–Њ—А—П–і–Њ—З–µ–љ–љ—Л–Љ–Є, —В–Њ –µ—Б—В—М –≤—Л–±–Њ—А–Ї–Є
{
1
,
2
,
4
,
6
}
{\displaystyle \{1,2,4,6\}}
{
4
,
2
,
6
,
1
}
{\displaystyle \{4,2,6,1\}}
–Ґ—А–µ–±—Г–µ—В—Б—П –њ–Њ—Б—З–Є—В–∞—В—М –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–±—Л—В–Є—П, –Ј–∞–Ї–ї—О—З–∞—О—Й–µ–≥–Њ—Б—П –≤ –Њ—В—Б—Г—В—Б—В–≤–Є–Є –њ–Њ–≤—В–Њ—А–µ–љ–Є–є –≤ –≤—Л–±–Њ—А–Ї–µ. –Т—Б–µ —А–∞—Б—З—С—В—Л –∞–љ–∞–ї–Њ–≥–Є—З–љ—Л –њ—А–Є–≤–µ–і—С–љ–љ—Л–Љ –≤—Л—И–µ .
–Т–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П —Г –і–≤—Г—Е —З–µ–ї–Њ–≤–µ–Ї, –≤—Е–Њ–і—П—Й–Є—Е –≤ –≥—А—Г–њ–њ—Г –Є–Ј n –ї—О–і–µ–є, –Љ–Њ–ґ–љ–Њ —В–∞–Ї–ґ–µ —А–∞—Б—Б—З–Є—В–∞—В—М —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —Д–Њ—А–Љ—Г–ї –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–Є [ 4] n —З–µ–ї–Њ–≤–µ–Ї –Љ–Њ–≥—Г—В –±—Л—В—М –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ—Л —Б—В—А–Њ–Ї–Њ–є, —Б–Њ—Б—В–Њ—П—Й–µ–є –Є–Ј n –±—Г–Ї–≤ —В–∞–Ї–Њ–≥–Њ –∞–ї—Д–∞–≤–Є—В–∞. –Я–Њ —Д–Њ—А–Љ—Г–ї–µ –•–∞—А—В–ї–Є , –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е —Б—В—А–Њ–Ї —А–∞–≤–љ–Њ
n
total
=
365
n
.
{\displaystyle n_{\text{total}}=365^{n}.}
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е —Б—В—А–Њ–Ї, –≤ –Ї–Њ—В–Њ—А—Л—Е –±—Г–Ї–≤—Л –љ–µ –њ–Њ–≤—В–Њ—А—П—О—В—Б—П (—А–∞–Ј–Љ–µ—Й–µ–љ–Є–µ –Є–Ј 365 –њ–Њ n ), —Б–Њ—Б—В–∞–≤–Є—В
n
unique
=
365
!
(
365
− вИТ -->
n
)
!
.
{\displaystyle n_{\text{unique}}={\frac {365!}{(365-n)!}}.}
–Х—Б–ї–Є —Б—В—А–Њ–Ї–Є –≤—Л–±–Є—А–∞—О—В—Б—П —Б–ї—Г—З–∞–є–љ–Њ (—Б —А–∞–≤–љ–Њ–Љ–µ—А–љ—Л–Љ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ–Љ ), –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –≤—Л–±–Њ—А–∞ —Б—В—А–Њ–Ї–Є, –≤ –Ї–Њ—В–Њ—А–Њ–є —Е–Њ—В—П –±—Л –і–≤–µ –±—Г–Ї–≤—Л —Б–Њ–≤–њ–∞–і—Г—В, —А–∞–≤–љ–∞
p
(
n
)
=
1
− вИТ -->
n
unique
n
total
=
1
− вИТ -->
365
!
(
365
− вИТ -->
n
)
!
365
n
{\displaystyle p(n)=1-{\frac {n_{\text{unique}}}{n_{\text{total}}}}=1-{\frac {\frac {365!}{(365-n)!}}{365^{n}}}}
n
⩽ в©љ -->
365
{\displaystyle n\leqslant 365}
p
(
n
)
=
1
{\displaystyle p(n)=1}
n
>
365
{\displaystyle n>365}
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ,
(
365
!
(
365
− вИТ -->
n
)
!
)
365
n
=
365
⋅ вЛЕ -->
364
⋅ вЛЕ -->
363
⋯ вЛѓ -->
(
365
− вИТ -->
n
+
1
)
365
n
=
{\displaystyle {\frac {\left({\frac {365!}{(365-n)!}}\right)}{365^{n}}}={\frac {365\cdot 364\cdot 363\cdots (365-n+1)}{365^{n}}}={}}
365
365
⋅ вЛЕ -->
364
365
⋅ вЛЕ -->
363
365
⋯ вЛѓ -->
365
− вИТ -->
n
+
1
365
=
{\displaystyle {\frac {365}{365}}\cdot {\frac {364}{365}}\cdot {\frac {363}{365}}\cdots {\frac {365-n+1}{365}}={}}
1
⋅ вЛЕ -->
(
1
− вИТ -->
1
365
)
⋅ вЛЕ -->
(
1
− вИТ -->
2
365
)
⋯ вЛѓ -->
(
1
− вИТ -->
n
− вИТ -->
1
365
)
,
{\displaystyle 1\cdot \left(1-{\frac {1}{365}}\right)\cdot \left(1-{\frac {2}{365}}\right)\cdots \left(1-{\frac {n-1}{365}}\right),}
–∞ —Н—В–Њ –≤—Л—А–∞–ґ–µ–љ–Є–µ —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–љ–Њ–Љ—Г –≤—Л—И–µ .
–Ґ–∞–Ї–ґ–µ –Њ–±—Й–µ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е —Б—В—А–Њ–Ї –Љ–Њ–ґ–љ–Њ —А–∞—Б—Б—З–Є—В–∞—В—М –њ–Њ —Д–Њ—А–Љ—Г–ї–µ –Ї–Њ–Љ–±–Є–љ–∞—В–Њ—А–Є–Ї–Є –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ —А–∞–Ј–Љ–µ—Й–µ–љ–Є–є —Б –њ–Њ–≤—В–Њ—А–µ–љ–Є—П–Љ–Є –Р (–њ–Њ–≤—В)вАѓn /365 = 365n
–Ш—Б–њ–Њ–ї—М–Ј—Г—П —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ —Н–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є –≤ —А—П–і –Ґ–µ–є–ї–Њ—А–∞
e
x
=
1
+
x
+
x
2
2
!
+
… вА¶ -->
,
{\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\ldots ,}
–њ—А–Є–≤–µ–і—С–љ–љ–Њ–µ –≤—Л—И–µ –≤—Л—А–∞–ґ–µ–љ–Є–µ –і–ї—П
p
¯ ¬ѓ -->
(
n
)
{\displaystyle {\bar {p}}(n)}
–∞–њ–њ—А–Њ–Ї—Б–Є–Љ–Є—А–Њ–≤–∞—В—М —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
p
¯ ¬ѓ -->
(
n
)
≈ вЙИ -->
1
⋅ вЛЕ -->
e
− вИТ -->
1
/
365
⋅ вЛЕ -->
e
− вИТ -->
2
/
365
⋯ вЛѓ -->
e
− вИТ -->
(
n
− вИТ -->
1
)
/
365
=
{\displaystyle {\bar {p}}(n)\approx 1\cdot e^{-1/365}\cdot e^{-2/365}\cdots e^{-(n-1)/365}=}
1
⋅ вЛЕ -->
e
− вИТ -->
(
1
+
2
+
⋯ вЛѓ -->
+
(
n
− вИТ -->
1
)
)
/
365
=
{\displaystyle 1\cdot e^{-(1+2+\cdots +(n-1))/365}=}
e
− вИТ -->
n
(
n
− вИТ -->
1
)
2
⋅ вЛЕ -->
365
.
{\displaystyle e^{-{\frac {n(n-1)}{2\cdot 365}}}.}
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ:
p
(
n
)
=
1
− вИТ -->
p
¯ ¬ѓ -->
(
n
)
≈ вЙИ -->
1
− вИТ -->
e
− вИТ -->
n
(
n
− вИТ -->
1
)
2
⋅ вЛЕ -->
365
.
{\displaystyle p(n)=1-{\bar {p}}(n)\approx 1-e^{-{\frac {n(n-1)}{2\cdot 365}}}.}
–У—А–∞—Д–Є–Ї–Є —Д—Г–љ–Ї—Ж–Є–Є p (n ) –Ч–∞–Љ–µ—В–Є–Љ, —З—В–Њ –Є —Г–њ—А–Њ—Й—С–љ–љ–∞—П –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—П
p
(
n
)
≈ вЙИ -->
1
− вИТ -->
e
− вИТ -->
n
2
2
⋅ вЛЕ -->
365
,
{\displaystyle p(n)\approx 1-e^{-{\frac {n^{2}}{2\cdot 365}}},}
–Ї–∞–Ї –≤–Є–і–љ–Њ –њ–Њ –≥—А–∞—Д–Є–Ї—Г, –≤—Б—С –µ—Й—С –і–∞—С—В –і–Њ—Б—В–∞—В–Њ—З–љ—Г—О —В–Њ—З–љ–Њ—Б—В—М.
–Я—А–Є–≤–µ–і—С–Љ –µ—Й—С –Њ–і–љ—Г –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є—О .
–Т–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ —Г –і–≤—Г—Е –ї—О–і–µ–є –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П –љ–µ —Б–Њ–≤–њ–∞–і–∞—О—В, —А–∞–≤–љ–∞ 364/365. –Т –≥—А—Г–њ–њ–µ –Є–Ј
n
{\displaystyle n}
C
(
n
,
2
)
=
n
(
n
− вИТ -->
1
)
2
{\displaystyle C(n,2)={\frac {n(n-1)}{2}}}
p
¯ ¬ѓ -->
(
n
)
{\displaystyle {\bar {p}}(n)}
–љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є —Н—В–Є—Е —Б–Њ–±—Л—В–Є–є –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–Є–±–ї–Є–ґ–µ–љ–∞ —З–Є—Б–ї–Њ–Љ
(
364
365
)
C
(
n
,
2
)
.
{\displaystyle \left({\frac {364}{365}}\right)^{C(n,2)}.}
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –њ–Њ–ї—Г—З–∞–µ–Љ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–µ –і–ї—П –Є—Б–Ї–Њ–Љ–Њ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є p (n )
p
(
n
)
≈ вЙИ -->
1
− вИТ -->
(
364
365
)
C
(
n
,
2
)
.
{\displaystyle p(n)\approx 1-\left({\frac {364}{365}}\right)^{C(n,2)}.}
–Ш—Б–њ–Њ–ї—М–Ј—Г—П –њ—А–Є–±–ї–Є–ґ–µ–љ–Є–µ –Я—Г–∞—Б—Б–Њ–љ–∞ –і–ї—П –±–Є–љ–Њ–Љ–∞ , –Є—Б—Е–Њ–і—П –Є–Ј –њ—А–µ–і—Л–і—Г—Й–µ–≥–Њ –њ—А–Є–±–ї–Є–ґ–µ–љ–Є—П –і–ї—П
p
(
n
)
{\displaystyle p(n)}
50 % :
Poi
вБ° -->
(
C
(
23
,
2
)
365
)
=
Poi
вБ° -->
(
253
365
)
≈ вЙИ -->
Poi
вБ° -->
(
0,693
2
)
;
{\displaystyle \operatorname {Poi} \left({\frac {C(23,2)}{365}}\right)=\operatorname {Poi} \left({\frac {253}{365}}\right)\approx \operatorname {Poi} (0{,}693\,2);}
P
(
{
X
>
0
}
)
=
1
− вИТ -->
P
(
{
X
=
0
}
)
=
1
− вИТ -->
e
− вИТ -->
0,693
2
=
1
− вИТ -->
0,499
998
=
0,500
002.
{\displaystyle \mathbb {P} \left(\{X>0\}\right)=1-\mathbb {P} \left(\{X=0\}\right)=1-e^{-0{,}693\,2}=1-0{,}499\,998=0{,}500\,002.}
–Ш–Ј –њ—А–Є–≤–µ–і—С–љ–љ–Њ–є —А–∞–љ–µ–µ —Д–Њ—А–Љ—Г–ї—Л
p
(
n
)
=
1
− вИТ -->
p
¯ ¬ѓ -->
(
n
)
≈ вЙИ -->
1
− вИТ -->
e
− вИТ -->
n
(
n
− вИТ -->
1
)
2
⋅ вЛЕ -->
365
{\displaystyle p(n)=1-{\bar {p}}(n)\approx 1-e^{-{\frac {n(n-1)}{2\cdot 365}}}}
n . –Ч–∞—В–µ–Љ –≤–Љ–µ—Б—В–Њ p (n )50 % (0,5). –Т —А–µ–Ј—Г–ї—М—В–∞—В–µ –њ–Њ–ї—Г—З–Є–Љ:
n
≈ вЙИ -->
1
2
+
1
4
− вИТ -->
2
⋅ вЛЕ -->
365
⋅ вЛЕ -->
ln
вБ° -->
0
,
5
=
22,999
9.
{\displaystyle n\approx {\frac {1}{2}}+{\sqrt {{\frac {1}{4}}-2\cdot 365\cdot \ln 0{,}5}}=22{,}9999.}
–°—Г—Й–µ—Б—В–≤—Г–µ—В –µ—Й—С –Њ–і–Є–љ —Б–њ–Њ—Б–Њ–± –Њ—Ж–µ–љ–Ї–Є n –њ—А–Є –≤–µ—А–Њ—П—В–љ–Њ—Б—В–Є 50 % .
–°–Њ–≥–ї–∞—Б–љ–Њ –і–Њ–Ї–∞–Ј–∞–љ–љ–Њ–Љ—Г –≤—Л—И–µ :
p
¯ ¬ѓ -->
(
n
)
=
1
− вИТ -->
p
(
n
)
=
∏ вИП -->
k
=
1
n
− вИТ -->
1
(
1
− вИТ -->
k
365
)
.
{\displaystyle {\bar {p}}(n)=1-p(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right).}
–Э–∞–є–і—С–Љ –љ–∞–Є–Љ–µ–љ—М—И–µ–µ n , –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ
p
(
n
)
>
1
2
{\displaystyle p(n)>{\frac {1}{2}}}
–Є–ї–Є, —З—В–Њ —В–Њ –ґ–µ —Б–∞–Љ–Њ–µ,
p
¯ ¬ѓ -->
(
n
)
<
1
2
.
{\displaystyle {\bar {p}}(n)<{\frac {1}{2}}.}
–Т–Њ—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Б—П –њ—А–Є–≤–µ–і—С–љ–љ–Њ–є –≤—Л—И–µ –∞–њ–њ—А–Њ–Ї—Б–Є–Љ–∞—Ж–Є–µ–є —Д—Г–љ–Ї—Ж–Є–Є
p
¯ ¬ѓ -->
(
n
)
{\displaystyle {\bar {p}}(n)}
—Н–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї—М–љ–Њ–є —Д—Г–љ–Ї—Ж–Є–µ–є :
p
¯ ¬ѓ -->
approx
(
n
)
=
∏ вИП -->
k
=
1
n
− вИТ -->
1
e
− вИТ -->
k
365
=
e
− вИТ -->
n
(
n
− вИТ -->
1
)
2
⋅ вЛЕ -->
365
.
{\displaystyle {\bar {p}}_{\text{approx}}(n)=\prod _{k=1}^{n-1}e^{\frac {-k}{365}}=e^{\frac {-n(n-1)}{2\cdot 365}}.}
–Я–Њ–і—Б—В–∞–≤–Є–≤
p
¯ ¬ѓ -->
approx
(
n
)
{\displaystyle {\bar {p}}_{\text{approx}}(n)}
p
¯ ¬ѓ -->
(
n
)
{\displaystyle {\bar {p}}(n)}
p
¯ ¬ѓ -->
(
n
)
<
1
2
{\displaystyle {\bar {p}}(n)<{\frac {1}{2}}}
e
− вИТ -->
n
(
n
− вИТ -->
1
)
2
⋅ вЛЕ -->
365
<
1
2
.
{\displaystyle e^{\frac {-n(n-1)}{2\cdot 365}}<{\frac {1}{2}}.}
–†–µ—И–∞—П –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ n , –њ–Њ–ї—Г—З–Є–Љ
n
2
− вИТ -->
n
>
2
⋅ вЛЕ -->
365
⋅ вЛЕ -->
ln
вБ° -->
2.
{\displaystyle n^{2}-n>2\cdot 365\cdot \ln 2.}
–Ю—В—Б—О–і–∞ –љ–∞–є–і—С–Љ n –Є –Њ–Ї—А—Г–≥–ї–Є–Љ –і–Њ —Ж–µ–ї–Њ–≥–Њ :
n = 23
–°—А–∞–≤–љ–Є–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М p (n )n —З–µ–ї–Њ–≤–µ–Ї –і–µ–љ—М —А–Њ–ґ–і–µ–љ–Є—П –Ї–∞–Ї–Њ–≥–Њ-–ї–Є–±–Њ —З–µ–ї–Њ–≤–µ–Ї–∞ –Є–Ј –≥—А—Г–њ–њ—Л —Б–Њ–≤–њ–∞–і—С—В —Б –і–љ—С–Љ —А–Њ–ґ–і–µ–љ–Є—П –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –Ј–∞—А–∞–љ–µ–µ –≤—Л–±—А–∞–љ–љ–Њ–≥–Њ —З–µ–ї–Њ–≤–µ–Ї–∞, –љ–µ –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—Й–µ–≥–Њ –≥—А—Г–њ–њ–µ. –≠—В–∞ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —А–∞–≤–љ–∞
q
(
n
)
=
1
− вИТ -->
(
365
− вИТ -->
1
365
)
n
.
{\displaystyle q(n)=1-\left({\frac {365-1}{365}}\right)^{n}.}
–°—А–∞–≤–љ–µ–љ–Є–µ –≥—А–∞—Д–Є–Ї–Њ–≤ —Д—Г–љ–Ї—Ж–Є–є p (n )q (n )–∞–±—Б—Ж–Є—Б—Б : –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —З–µ–ї–Њ–≤–µ–Ї n .–Њ—А–і–Є–љ–∞—В : –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М.p (n )n —З–µ–ї–Њ–≤–µ–Ї –Ї–∞–Ї –Љ–Є–љ–Є–Љ—Г–Љ —Г –і–≤—Г—Е –Є–Ј –љ–Є—Е –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П —Б–Њ–≤–њ–∞–і—Г—В.q (n )n —З–µ–ї–Њ–≤–µ–Ї –і–µ–љ—М —А–Њ–ґ–і–µ–љ–Є—П –Ї–∞–Ї–Њ–≥–ЊвАС–ї–Є–±–Њ —З–µ–ї–Њ–≤–µ–Ї–∞ –Є–Ј –≥—А—Г–њ–њ—Л —Б–Њ–≤–њ–∞–і—С—В —Б –і–љ—С–Љ —А–Њ–ґ–і–µ–љ–Є—П –љ–µ–Ї–Њ—В–Њ—А–Њ–≥–Њ –Ј–∞—А–∞–љ–µ–µ –≤—Л–±—А–∞–љ–љ–Њ–≥–Њ —З–µ–ї–Њ–≤–µ–Ї–∞, –љ–µ –њ—А–Є–љ–∞–і–ї–µ–ґ–∞—Й–µ–≥–Њ –≥—А—Г–њ–њ–µ. –Я–Њ–і—Б—В–∞–≤–ї—П—П n = 23q (n ) вЙИ 6,12 %q (n )50 % , —З–Є—Б–ї–Њ –ї—О–і–µ–є –≤ –≥—А—Г–њ–њ–µ –і–Њ–ї–ґ–љ–Њ –±—Л—В—М –љ–µ –Љ–µ–љ–µ–µ 253 (q (252) вЙИ 49,91 %q (253) вЙИ 50,05 %365/2 = 182,5 ); —В–∞–Ї –њ—А–Њ–Є—Б—Е–Њ–і–Є—В –Є–Ј-–Ј–∞ —В–Њ–≥–Њ, —З—В–Њ —Г –Њ—Б—В–∞–ї—М–љ—Л—Е —З–ї–µ–љ–Њ–≤ –≥—А—Г–њ–њ—Л –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П –Љ–Њ–≥—Г—В —Б–Њ–≤–њ–∞–і–∞—В—М –Љ–µ–ґ–і—Г —Б–Њ–±–Њ–є, –Є —Н—В–Њ —Г–Љ–µ–љ—М—И–∞–µ—В –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М q (n )P (A + B ) = P (A ) + P (B ) вИТ P (AB ) –Є —В. –і —Б –Ї–∞–ґ–і—Л–Љ –і–Њ–±–∞–≤–ї–µ–љ–Є–µ–Љ –љ–Њ–≤–Њ–≥–Њ —Б–ї–∞–≥–∞–µ–Љ–Њ–≥–Њ.
–Ю–њ–Є—Б–∞–љ–љ–∞—П –Ј–∞–і–∞—З–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М —Б—Д–Њ—А–Љ—Г–ї–Є—А–Њ–≤–∞–љ–∞ –≤ –Њ–±—Й–µ–Љ –≤–Є–і–µ:
–і–∞–љ—Л —Б–ї—Г—З–∞–є–љ—Л–µ —З–Є—Б–ї–∞;
—Б–ї—Г—З–∞–є–љ—Л–µ —З–Є—Б–ї–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ –≤ –і–Є–∞–њ–∞–Ј–Њ–љ–µ –Њ—В 1 –і–Њ d ;
n вАФ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —Б–ї—Г—З–∞–є–љ—Л—Е —З–Є—Б–µ–ї;–Њ–њ—А–µ–і–µ–ї–Є—В—М p ( n ; d )–≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ —Б–Њ–≤–њ–∞–і—Г—В —Е–Њ—В—П –±—Л –і–≤–∞ —З–Є—Б–ї–∞ –Є–Ј –Ј–∞–і–∞–љ–љ—Л—Е. –Х—Б–ї–Є —А–∞—Б—Б—Г–ґ–і–∞—В—М —В–∞–Ї–Є–Љ –ґ–µ –Њ–±—А–∞–Ј–Њ–Љ, –Ї–∞–Ї –Њ–њ–Є—Б–∞–љ–Њ –≤—Л—И–µ , –Љ–Њ–ґ–љ–Њ –њ–Њ–ї—Г—З–Є—В—М –Њ–±—Й–Є–µ —А–µ—И–µ–љ–Є—П:
p
(
n
;
d
)
=
{
1
− вИТ -->
∏ вИП -->
k
=
1
n
− вИТ -->
1
(
1
− вИТ -->
k
d
)
n
≤ вЙ§ -->
d
1
n
>
d
;
{\displaystyle p(n;d)={\begin{cases}1-\prod _{k=1}^{n-1}\left(1-{k \over d}\right)&n\leq d\\1&n>d\end{cases}};}
p
(
n
;
d
)
≈ вЙИ -->
1
− вИТ -->
e
− вИТ -->
(
n
(
n
− вИТ -->
1
)
)
/
2
d
;
{\displaystyle p(n;d)\approx 1-e^{-(n(n-1))/2d};}
q
(
n
;
d
)
=
1
− вИТ -->
(
d
− вИТ -->
1
d
)
n
.
{\displaystyle q(n;d)=1-\left({\frac {d-1}{d}}\right)^{n}.}
–Ю–±—А–∞—В–љ–∞—П –Ј–∞–і–∞—З–∞:
–і–∞–љ–∞ p вАФ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ —Б–Њ–≤–њ–∞–і–∞—О—В —Е–Њ—В—П –±—Л –і–≤–∞ —Б–ї—Г—З–∞–є–љ—Л—Е —З–Є—Б–ї–∞;
–Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ —Б–ї—Г—З–∞–є–љ—Л–µ —З–Є—Б–ї–∞ —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ –≤ –і–Є–∞–њ–∞–Ј–Њ–љ–µ –Њ—В 1 –і–Њ d ;
–љ–∞–є—В–Є n (p ;d ) –†–µ—И–µ–љ–Є–µ:
n
(
p
;
d
)
≈ вЙИ -->
2
d
⋅ вЛЕ -->
ln
вБ° -->
(
1
1
− вИТ -->
p
)
.
{\displaystyle n(p;d)\approx {\sqrt {2d\cdot \ln \left({1 \over 1-p}\right)}}.}
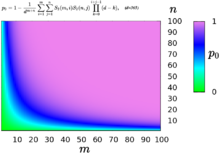
–Т–µ—А–Њ—П—В–љ–Њ—Б—В—М —Б–Њ–≤–њ–∞–і–µ–љ–Є—П –і–љ—П —А–Њ–ґ–і–µ–љ–Є—П —Е–Њ—В—П –±—Л —Г –Њ–і–љ–Њ–≥–Њ –Љ—Г–ґ—З–Є–љ—Л –Є —Г –Њ–і–љ–Њ–є –ґ–µ–љ—Й–Є–љ—Л –Т—Л—И–µ –њ–∞—А–∞–і–Њ–Ї—Б –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П –±—Л–ї –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ –і–ї—П –Њ–і–љ–Њ–≥–Њ ¬Ђ—В–Є–њ–∞¬ї –ї—О–і–µ–є. –Ь–Њ–ґ–љ–Њ –Њ–±–Њ–±—Й–Є—В—М –Ј–∞–і–∞—З—Г, –≤–≤–µ–і—П –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ ¬Ђ—В–Є–њ–Њ–≤¬ї, –љ–∞–њ—А–Є–Љ–µ—А, —А–∞–Ј–і–µ–ї–Є–≤ –ї—О–і–µ–є –љ–∞ –Љ—Г–ґ—З–Є–љ (m ) –Є –ґ–µ–љ—Й–Є–љ (n ). –Я–Њ–і—Б—З–Є—В–∞–µ–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ —Е–Њ—В—П –±—Л —Г –Њ–і–љ–Њ–є –ґ–µ–љ—Й–Є–љ—Л –Є —Г –Њ–і–љ–Њ–≥–Њ –Љ—Г–ґ—З–Є–љ—Л —Б–Њ–≤–њ–∞–і–∞—О—В –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П (—Б–Њ–≤–њ–∞–і–µ–љ–Є–µ –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П —Г –і–≤—Г—Е –ґ–µ–љ—Й–Є–љ –Є–ї–Є —Г –і–≤—Г—Е –Љ—Г–ґ—З–Є–љ –љ–µ —Г—З–Є—В—Л–≤–∞—О—В—Б—П):
p
0
=
1
− вИТ -->
1
d
m
+
n
∑ вИС -->
i
=
1
m
∑ вИС -->
j
=
1
n
S
2
(
m
,
i
)
S
2
(
n
,
j
)
∏ вИП -->
k
=
0
i
+
j
− вИТ -->
1
(
d
− вИТ -->
k
)
,
{\displaystyle p_{0}=1-{\frac {1}{d^{m+n}}}\sum _{i=1}^{m}\sum _{j=1}^{n}S_{2}(m,i)S_{2}(n,j)\prod _{k=0}^{i+j-1}(d-k),}
–≥–і–µ d = 365S 2 () вАФ —З–Є—Б–ї–∞ –°—В–Є—А–ї–Є–љ–≥–∞ –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞ . –Ш–љ—В–µ—А–µ—Б–љ–Њ, —З—В–Њ –љ–µ—В –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ–≥–Њ –Њ—В–≤–µ—В–∞ –љ–∞ –≤–Њ–њ—А–Њ—Б –Њ –≤–µ–ї–Є—З–Є–љ–µ n +m
–Ф—А—Г–≥–Њ–µ –Њ–±–Њ–±—Й–µ–љ–Є–µ –њ–∞—А–∞–і–Њ–Ї—Б–∞ –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П —Б–Њ—Б—В–Њ–Є—В –≤ –њ–Њ—Б—В–∞–љ–Њ–≤–Ї–µ –Ј–∞–і–∞—З–Є –Њ —В–Њ–Љ, —Б–Ї–Њ–ї—М–Ї–Њ —В—А–µ–±—Г–µ—В—Б—П —З–µ–ї–Њ–≤–µ–Ї –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –љ–∞–ї–Є—З–Є—П –≤ –≥—А—Г–њ–њ–µ –ї—О–і–µ–є, –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П –Ї–Њ—В–Њ—А—Л—Е —А–∞–Ј–ї–Є—З–∞—О—В—Б—П –љ–µ –±–Њ–ї–µ–µ —З–µ–Љ –љ–∞ –Њ–і–Є–љ –і–µ–љ—М (–Є–ї–Є –љ–∞ –і–≤–∞, —В—А–Є –і–љ—П –Є —В–∞–Ї –і–∞–ї–µ–µ), –њ—А–µ–≤—Л—Б–Є–ї–∞ 50 % . –Я—А–Є —А–µ—И–µ–љ–Є–Є —Н—В–Њ–є –Ј–∞–і–∞—З–Є –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –њ—А–Є–љ—Ж–Є–њ –≤–Ї–ї—О—З–µ–љ–Є—П-–Є—Б–Ї–ї—О—З–µ–љ–Є—П . –†–µ–Ј—Г–ї—М—В–∞—В (–Њ–њ—П—В—М-—В–∞–Ї–Є –≤ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–Є, —З—В–Њ –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ ) –њ–Њ–ї—Г—З–∞–µ—В—Б—П —Б–ї–µ–і—Г—О—Й–Є–Љ:
–Ь–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–µ —А–∞–Ј–ї–Є—З–Є–µ –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П, –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –і–љ–µ–є
–Э–µ–Њ–±—Е–Њ–і–Є–Љ–Њ–µ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –ї—О–і–µ–є
1
23
2
14
3
11
4
9
5
8
6
8
7
7
8
7
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М —В–Њ–≥–Њ, —З—В–Њ –і–∞–ґ–µ –≤ –≥—А—Г–њ–њ–µ –Є–Ј 7 —З–µ–ї–Њ–≤–µ–Ї –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П —Е–Њ—В—П –±—Л —Г –і–≤—Г—Е –Є–Ј –љ–Є—Е –±—Г–і—Г—В —А–∞–Ј–ї–Є—З–∞—В—М—Б—П –љ–µ –±–Њ–ї–µ–µ —З–µ–Љ –љ–∞ –љ–µ–і–µ–ї—О, –њ—А–µ–≤—Л—И–∞–µ—В 50 % .
–Я–∞—А–∞–і–Њ–Ї—Б –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П –≤ –Њ–±—Й–µ–Љ –≤–Є–і–µ –њ—А–Є–Љ–µ–љ–Є–Љ –Ї —Е–µ—И-—Д—Г–љ–Ї—Ж–Є—П–Љ : –µ—Б–ї–Є —Е–µ—И-—Д—Г–љ–Ї—Ж–Є—П –≥–µ–љ–µ—А–Є—А—Г–µ—В N вАС–±–Є—В–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ, —В–Њ —З–Є—Б–ї–Њ —Б–ї—Г—З–∞–є–љ—Л—Е –≤—Е–Њ–і–љ—Л—Е –і–∞–љ–љ—Л—Е, –і–ї—П –Ї–Њ—В–Њ—А—Л—Е —Е–µ—И-–Ї–Њ–і—Л —Б –±–Њ–ї—М—И–Њ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О –і–∞–і—Г—В –Ї–Њ–ї–ї–Є–Ј–Є—О (—В–Њ –µ—Б—В—М –љ–∞–є–і—Г—В—Б—П —А–∞–≤–љ—Л–µ —Е–µ—И-–Ї–Њ–і—Л, –њ–Њ–ї—Г—З–µ–љ–љ—Л–µ –љ–∞ —А–∞–Ј–љ—Л—Е –≤—Е–Њ–і–љ—Л—Е –і–∞–љ–љ—Л—Е), —А–∞–≤–љ–Њ –љ–µ 2N N /2–∞—В–∞–Ї–∞ вАЮ–і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—ПвАЬ ¬ї.
N
–Ъ–Њ–ї–Є—З–µ—Б—В–≤–Њ —А–∞–Ј–ї–Є—З–љ—Л—Е –≤—Л—Е–Њ–і–љ—Л—Е —Ж–µ–њ–Њ—З–µ–Ї (2N )
–Т–µ—А–Њ—П—В–љ–Њ—Б—В—М —Е–Њ—В—П –±—Л –Њ–і–љ–Њ–є –Ї–Њ–ї–ї–Є–Ј–Є–Є (p )
10вИТ18
10вИТ15
10вИТ12
10вИТ9
10вИТ6
0,1 %
1 %
25 %
50 %
75 %
32
4,3 √Ч 109
2
2
2
2,9
93
2,9 √Ч 10¬≥
9,3 √Ч 10¬≥
5,0 √Ч 10вБі
7,7 √Ч 10вБі
1,1 √Ч 10вБµ
64
1,8 √Ч 1019
6,1
1,9 √Ч 10¬≤
6,1 √Ч 10¬≥
1,9 √Ч 10вБµ
6,1 √Ч 10вБґ
1,9 √Ч 10вБЄ
6,1 √Ч 10вБЄ
3,3 √Ч 10вБє
5,1 √Ч 10вБє
7,2 √Ч 10вБє
128
3,4 √Ч 1038
2,6 √Ч 1010
8,2 √Ч 1011
2,6 √Ч 1013
8,2 √Ч 1014
2,6 √Ч 1016
8,3 √Ч 1017
2,6 √Ч 1018
1,4 √Ч 1019
2,2 √Ч 1019
3,1 √Ч 1019
256
1,2 √Ч 1077
4,8 √Ч 1029
1,5 √Ч 1031
4,8 √Ч 1032
1,5 √Ч 1034
4,8 √Ч 1035
1,5 √Ч 1037
4,8 √Ч 1037
2,6 √Ч 1038
4,0 √Ч 1038
5,7 √Ч 1038
384
3,9 √Ч 10115
8,9 √Ч 1048
2,8 √Ч 1050
8,9 √Ч 1051
2,8 √Ч 1053
8,9 √Ч 1054
2,8 √Ч 1056
8,9 √Ч 1056
4,8 √Ч 1057
7,4 √Ч 1057
1,0 √Ч 1058
512
1,3 √Ч 10154
1,6 √Ч 1068
5,2 √Ч 1069
1,6 √Ч 1071
5,2 √Ч 1072
1,6 √Ч 1074
5,2 √Ч 1075
1,6 √Ч 1076
8,8 √Ч 1076
1,4 √Ч 1077
1,9 √Ч 1077
–Т –±–µ–ї—Л—Е —П—З–µ–є–Ї–∞—Е —Г–Ї–∞–Ј–∞–љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ —З–µ–ї–Њ–≤–µ–Ї –≤ –≥—А—Г–њ–њ–µ, –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ –Ї–Њ–ї–ї–Є–Ј–Є—П –њ—А–Њ–Є–Ј–Њ–є–і—С—В —Б –Ј–∞–і–∞–љ–љ–Њ–є –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М—О (–њ–Њ –∞–љ–∞–ї–Њ–≥–Є–Є —Б –њ–∞—А–∞–і–Њ–Ї—Б–Њ–Љ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –≤—Л—Е–Њ–і–љ—Л—Е —Ж–µ–њ–Њ—З–µ–Ї —А–∞–≤–љ–Њ 365).
–°—Е–Њ–і–љ—Л–є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–є –∞–њ–њ–∞—А–∞—В –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –і–ї—П –Њ—Ж–µ–љ–Ї–Є —А–∞–Ј–Љ–µ—А–∞ –њ–Њ–њ—Г–ї—П—Ж–Є–Є —А—Л–± , –Њ–±–Є—В–∞—О—Й–Є—Е –≤ –Њ–Ј—С—А–∞—Е . –Ь–µ—В–Њ–і –љ–∞–Ј—Л–≤–∞–µ—В—Б—П ¬Ђcapture-recapture¬ї (¬Ђ–њ–Њ–є–Љ–∞—В—М вАФ –њ–Њ–є–Љ–∞—В—М —Б–љ–Њ–≤–∞¬ї). –Ф–µ–є—Б—В–≤–Є—В–µ–ї—М–љ–Њ, –µ—Б–ї–Є –Ї–∞–ґ–і—Г—О –њ–Њ–є–Љ–∞–љ–љ—Г—О —А—Л–±—Г –њ–Њ–Љ–µ—З–∞—В—М –Є –Њ—В–њ—Г—Б–Ї–∞—В—М, —В–Њ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М –њ–Њ–є–Љ–∞—В—М –њ–Њ–Љ–µ—З–µ–љ–љ—Г—О —А—Л–±—Г –±—Г–і–µ—В —А–∞—Б—В–Є –љ–µ–ї–Є–љ–µ–є–љ–Њ (–≤ —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–Є–Є —Б –њ—А–Є–≤–µ–і—С–љ–љ—Л–Љ –≤—Л—И–µ –≥—А–∞—Д–Є–Ї–Њ–Љ) —Б —А–Њ—Б—В–Њ–Љ –Ї–Њ–ї–Є—З–µ—Б—В–≤–∞ –њ–Њ–њ—Л—В–Њ–Ї. –†–∞–Ј–Љ–µ—А –њ–Њ–њ—Г–ї—П—Ж–Є–Є –≥—А—Г–±–Њ –Љ–Њ–ґ–µ—В –±—Л—В—М –Њ—Ж–µ–љ—С–љ –Ї–∞–Ї –Ї–≤–∞–і—А–∞—В —З–Є—Б–ї–∞ –њ–Њ–њ—Л—В–Њ–Ї, —Б–Њ–≤–µ—А—И–∞–µ–Љ—Л—Е –і–Њ –≤—Л–ї–∞–≤–ї–Є–≤–∞–љ–Є—П –њ–µ—А–≤–Њ–є –њ–Њ–Љ–µ—З–µ–љ–љ–Њ–є —А—Л–±—Л.
–†–µ—И–µ–љ–Є–µ –Ј–∞–і–∞—З–Є –≤ –Њ–±—Й–µ–Љ –≤–Є–і–µ –љ–∞—Е–Њ–і–Є—В –њ—А–Є–Љ–µ–љ–µ–љ–Є–µ –≤–Њ –Љ–љ–Њ–≥–Є—Е —А–∞–Ј–і–µ–ї–∞—Е –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є , –љ–∞–њ—А–Є–Љ–µ—А, –≤ –љ–µ–і–µ—В–µ—А–Љ–Є–љ–Є—А–Њ–≤–∞–љ–љ—Л—Е –∞–ї–≥–Њ—А–Є—В–Љ–∞—Е —Д–∞–Ї—В–Њ—А–Є–Ј–∞—Ж–Є–Є . –Ґ–∞–Ї, –Њ–і–љ–Њ –Є–Ј —Б–∞–Љ—Л—Е –њ—А–Њ—Б—В—Л—Е –Њ–±—К—П—Б–љ–µ–љ–Є–є ѕБ-–Љ–µ—В–Њ–і–∞ –Я–Њ–ї–ї–∞—А–і–∞ –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ –Њ–±—К—П—Б–љ–µ–љ–Є—О –њ–∞—А–∞–і–Њ–Ї—Б–∞ –і–љ–µ–є —А–Њ–ґ–і–µ–љ–Є—П: –і–Њ—Б—В–∞—В–Њ—З–љ–Њ –Є–Љ–µ—В—М –њ—А–Є–Љ–µ—А–љ–Њ
p
{\displaystyle {\sqrt {p}}}
n
=
p
q
{\displaystyle n=pq}
p
<
q
{\displaystyle p<q}
gcd
(
|
x
− вИТ -->
y
|
,
n
)
>
1
{\displaystyle \gcd \left(|x-y|,n\right)>1}
n .
–Я–Њ–Є—Б–Ї –љ–∞–Є–Љ–µ–љ—М—И–µ–≥–Њ —З–Є—Б–ї–∞ n , –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М p (n ) –±–Њ–ї—М—И–µ –Ј–∞–і–∞–љ–љ–Њ–≥–Њ —З–Є—Б–ї–∞ p . –Я–Њ–Є—Б–Ї –љ–∞–Є–±–Њ–ї—М—И–µ–≥–Њ —З–Є—Б–ї–∞ n , –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М p (n )p . –Я–Њ–ї—М–Ј—Г—П—Б—М —Д–Њ—А–Љ—Г–ї–Њ–є, –њ—А–Є–≤–µ–і—С–љ–љ–Њ–є –≤—Л—И–µ, –њ–Њ–ї—Г—З–∞–µ–Љ:
n
(
p
;
365
)
≈ вЙИ -->
2
⋅ вЛЕ -->
365
⋅ вЛЕ -->
ln
вБ° -->
(
1
1
− вИТ -->
p
)
.
{\displaystyle n(p;365)\approx {\sqrt {2\cdot 365\cdot \ln \left({1 \over 1-p}\right)}}.}
p
n
n вЖУ
p (n вЖУ)
n вЖС
p (n вЖС)
0,01
0,14178вИЪ365 = 2,70864
2
0,00274
3
0,00820
0,05
0,32029вИЪ365 = 6,11916
6
0,04046
7
0,05624
0,1
0,45904вИЪ365 = 8,77002
8
0,07434
9
0,09462
0,2
0,66805вИЪ365 = 12,76302
12
0,16702
13
0,19441
0,3
0,84460вИЪ365 = 16,13607
16
0,28360
17
0,31501
0,5
1,17741вИЪ365 = 22,49439
22
0,47570
23
0,50730
0,7
1,55176вИЪ365 = 29,64625
29
0,68097
30
0,70632
0,8
1,79412вИЪ365 = 34,27666
34
0,79532
35
0,81438
0,9
2,14597вИЪ365 = 40,99862
40
0,89123
41
0,90315
0,95
2,44775вИЪ365 = 46,76414
46
0,94825
47
0,95477
0,99
3,03485вИЪ365 = 57,98081
57
0,99012
58
0,99166
–Я—Г—Б—В—М –≤ –Ї–Њ–Љ–љ–∞—В–µ –љ–∞—Е–Њ–і—П—В—Б—П n - 1g (n )n , –њ—А–Є –Ї–Њ—В–Њ—А–Њ–Љ –Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є g (n )
–†–µ—И–µ–љ–Є–µ —Б–≤–Њ–і–Є—В—Б—П –Ї –љ–∞—Е–Њ–ґ–і–µ–љ–Є—О –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П –≤—Л—А–∞–ґ–µ–љ–Є—П
p (n ) - p (n -1)–Ш—Б–њ–Њ–ї—М–Ј—Г—П –њ—А–Є–≤–µ–і—С–љ–љ—Г—О –≤—Л—И–µ —Д–Њ—А–Љ—Г–ї—Г –і–ї—П p (n )n = 20
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ –і—А—Г–≥—Г—О –Ј–∞–і–∞—З—Г. –°–Ї–Њ–ї—М–Ї–Њ –≤ —Б—А–µ–і–љ–µ–Љ –љ—Г–ґ–љ–Њ –ї—О–і–µ–є –і–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л —Е–Њ—В—П –±—Л —Г –і–≤—Г—Е –Є–Ј –љ–Є—Е —Б–Њ–≤–њ–∞–ї–Є –і–љ–Є —А–Њ–ґ–і–µ–љ–Є—П?
–≠—В–∞ –њ—А–Њ–±–ї–µ–Љ–∞ –Є–Љ–µ–ї–∞ –Њ—В–љ–Њ—И–µ–љ–Є–µ –Ї –∞–ї–≥–Њ—А–Є—В–Љ–∞–Љ —Е–µ—И–Є—А–Њ–≤–∞–љ–Є—П –Є –±—Л–ї–∞ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–∞ –Ф–Њ–љ–∞–ї—М–і–Њ–Љ –Ъ–љ—Г—В–Њ–Љ .
–Ю–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П, —З—В–Њ –Є–љ—В–µ—А–µ—Б—Г—О—Й–∞—П –љ–∞—Б —Б–ї—Г—З–∞–є–љ–∞—П –≤–µ–ї–Є—З–Є–љ–∞ –Є–Љ–µ–µ—В –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–µ –Њ–ґ–Є–і–∞–љ–Є–µ , —А–∞–≤–љ–Њ–µ
n
¯ ¬ѓ -->
=
1
+
Q
(
M
)
,
{\displaystyle {\overline {n}}\,=\,1+Q(M),}
–≥–і–µ
Q
(
M
)
=
∑ вИС -->
k
=
1
M
M
!
(
M
− вИТ -->
k
)
!
M
k
.
{\displaystyle Q(M)=\sum _{k=1}^{M}{\frac {M!}{(M-k)!M^{k}}}.}
–§—Г–љ–Ї—Ж–Є—П
Q
(
M
)
=
1
+
M
− вИТ -->
1
M
+
(
M
− вИТ -->
1
)
(
M
− вИТ -->
2
)
M
2
+
⋯ вЛѓ -->
+
(
M
− вИТ -->
1
)
(
M
− вИТ -->
2
)
⋯ вЛѓ -->
1
M
M
− вИТ -->
1
{\displaystyle Q(M)\,=\,1+{\frac {M-1}{M}}+{\frac {(M-1)(M-2)}{M^{2}}}+\cdots +{\frac {(M-1)(M-2)\cdots 1}{M^{M-1}}}}
–±—Л–ї–∞ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–∞ –†–∞–Љ–∞–љ—Г–і–ґ–∞–љ–Њ–Љ . –Ю–љ –ґ–µ –њ–Њ–ї—Г—З–Є–ї –і–ї—П —Н—В–Њ–є —Д—Г–љ–Ї—Ж–Є–Є —Б–ї–µ–і—Г—О—Й–µ–µ –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Њ–µ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є–µ :
Q
(
M
)
∼ вИЉ -->
π ѕА -->
M
2
− вИТ -->
1
3
+
1
12
π ѕА -->
2
M
− вИТ -->
4
135
M
+
⋯ вЛѓ -->
.
{\displaystyle Q(M)\sim {\sqrt {\frac {\pi M}{2}}}-{\frac {1}{3}}+{\frac {1}{12}}{\sqrt {\frac {\pi }{2M}}}-{\frac {4}{135M}}+\cdots .}
–Я—А–Є M = 365
n
¯ ¬ѓ -->
=
1
+
Q
(
M
)
≈ вЙИ -->
24
,
61658.
{\displaystyle {\overline {n}}\,=\,1+Q(M)\approx 24,61658.}
–≠—В–Њ —З–Є—Б–ї–Њ –љ–µ–Љ–љ–Њ–≥–Њ –±–Њ–ї—М—И–µ, —З–µ–Љ —З–Є—Б–ї–Њ –ї—О–і–µ–є, –Њ–±–µ—Б–њ–µ—З–Є–≤–∞—О—Й–Є—Е –≤–µ—А–Њ—П—В–љ–Њ—Б—В—М 50 % . –Ъ–∞–Ї –љ–Є —Г–і–Є–≤–Є—В–µ–ї—М–љ–Њ, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ–µ —З–Є—Б–ї–Њ –ї—О–і–µ–є —А–∞–≤–љ–Њ M + 1 = 366
–°—Б—Л–ї–Ї–Є –љ–∞ –≤–љ–µ—И–љ–Є–µ —А–µ—Б—Г—А—Б—Л
–Ґ–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–µ —Б–∞–є—В—Л
–°–ї–Њ–≤–∞—А–Є –Є —Н–љ—Ж–Є–Ї–ї–Њ–њ–µ–і–Є–Є