–Ь–µ—В–Њ–і –Љ–Є–љ–Є–Љ–∞–ї—М–љ—Л—Е –Є–Ј–Љ–µ–љ–µ–љ–Є–є
|
Read other articles:

Nell FranzenFranzen ca. 1922Lahir(1889-11-17)17 November 1889[1]Portland, Oregon, A.S.Meninggal21 Agustus 1973(1973-08-21) (umur 83)Orange, California, A.S.MakamForest Lawn Memorial Park, Glendale, California34¬∞07вА≤31вА≥N 118¬∞14вА≤37вА≥E / 34.1252¬∞N 118.2437¬∞E / 34.1252; 118.2437PekerjaanAktrisTahun aktif1913вАУ1924 Nell W. Franzen (17 November 1889 – 21 Agustus 1973) adalah seorang aktris film dan panggung Amerika dari era bisu....

Provinsi Ise (дЉКеЛҐеЫљcode: ja is deprecated , ise no kuni) atau dikenal sebagai Seishu (еЛҐеЈЮcode: ja is deprecated , seish≈Ђ) adalah nama provinsi lama Jepang yang menempati hampir seluruh wilayah prefektur Mie sekarang. Ise berbatasan dengan provinsi Iga, Kii, Mino, Omi, Owari, Shima, dan provinsi Yamato. Ibu kota berada di Suzuka. Kota istana yang terbesar adalah kota yang sekarang dikenal sebagai Tsu, walaupun ada juga kota sekeliling istana yang berkembang di tempat-tempat yang memil...

Karakteristik kawahKawah Anville dari Apollo 11. foto NASA.Koordinat1.9° U, 49.5° TDiameter11 kmKedalamanTidak diketahuiKolongitud311¬∞ saat Matahari terbitEponimJean-Baptiste d'Anvillelbs Anville adalah sebuah kawah Bulan soliter yang relatif kecil berlokasi di bagian utara Mare Fecunditatis. Kawah ini berbentuk cangkir yang sirkuler dengan tepian yang tajam. Kawah ini bernama 'Taruntius G' sebelum diberi nama oleh IAU. Di sebelah utara-baratdaya, di ujung mare, terletak ...

American college football season 1912 Florida Gators footballThe 1912 Gators practicing on the UF campusBacardi Bowl, W 28вАУ0 vs. Vedado Tennis ClubConferenceSouthern Intercollegiate Athletic AssociationRecord5вАУ2вАУ1 (0вАУ2вАУ1 SIAA)Head coachGeorge E. Pyle (4th season)CaptainSam BuieHome stadiumUniversity Athletic FieldSeasons← 19111913 → 1912 Southern Intercollegiate Athletic Association football standings vte Conf Overall Team W L T W ...

British news publishing company A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (May 2023) (Learn how and when to remove this template message) National World PLCLeeds head office of National World PLCTrade nameNational WorldFormerlyJPIMedia LtdCompany typePublic companyIndustryDigital MediaPredecessorJohnston...

Chronologie de la France вЧДвЧД 1660 1661 1662 1663 1664 1665 1666 1667 1668 вЦЇвЦЇ Chronologies 12 mai : premi√®re repr√©sentation du Tartuffe. Frontispice du Tartuffe par Pierre Brissart (1682).Donn√©es cl√©s 1661 1662 1663 1664 1665 1666 1667D√©cennies :1630 1640 1650 1660 1670 1680 1690Si√®cles :XVe XVIe XVIIe XVIIIe XIXeMill√©naires :-Ier Ier IIe IIIe Chronologies th√©matiques Art Architecture, Arts plastiques (Dessin, ...

SarsaSarsa in 2019Background informationBirth nameMarta MarkiewiczAlso known as Sarsa Markiewicz Born (1989-06-13) 13 June 1989 (age 34)S≈Вupsk, PolandGenres Electropop indie pop Occupation(s) Singer songwriter record producer composer Instrument(s) Vocals guitar ukulele piano Years active2010вАУpresentLabelsUniversal Music PolskaWebsitehttps://www.sarsa.com.pl/Musical artist Sarsa (2015) Marta Markiewicz (born 13 June 1989), better known as Sarsa or Sarsa Markiewicz, is a Polish singer,...

Styphnolobium Dedaunan styphnolobium japonicum Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Rosidae Ordo: Fabales Famili: Fabaceae Subfamili: Faboideae Genus: StyphnolobiumSchott Spesies tipe Styphnolobium japonicum(L.) Schott Spesies Lihat teks Sinonim Sophora sect. Styphnolobium (Schott) Yaklovev Styphnolobium adalah genus kecil dari tiga atau empat spesies pohon kecil dan perdu dalam subfamili Faboideae dari keluarga kacang po...

Department of the state government of Oregon, United States Oregon Department of TransportationAgency overviewFormed1969Preceding agenciesOregon State Highway CommissionOregon State Highway DepartmentJurisdictionOregonHeadquarters355 Capitol Street NE, Salem, Oregon 97301-3871Agency executiveKris Strickler, DirectorParent agencyOregon Transportation CommissionWebsiteoregon.gov/ODOT The Oregon Department of Transportation (ODOT) is a department of the state government of the U.S. state of Oreg...

–•—А–∞–Љ–Њ–≤—Л–є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–Я—А—Н–∞—Е–≤–Є—Е–µ–∞–Ї—Е–Љ–µ—А. бЮФбЯТбЮЪбЮґбЮЯбЮґбЮСбЮЦбЯТбЮЪбЯЗбЮЬбЮЈбЮ†бЮґбЮЪ 14¬∞23вА≤26вА≥ —Б. —И. 104¬∞40вА≤49вА≥ –≤. –і.HG–ѓO –°—В—А–∞–љ–∞ –Ъ–∞–Љ–±–Њ–і–ґ–∞ –Ь–µ—Б—В–Њ–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –Я—А—Н–∞—Е–≤–Є—Е–µ–∞ –Ґ–Є–њ –Ј–і–∞–љ–Є—П —Е—А–∞–Љ –®–Є–≤—Л –Ю—Б–љ–Њ–≤–∞—В–µ–ї—М –ѓ—И–Њ–≤–∞—А–Љ–∞–љ I –Ф–∞—В–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є—П 893 –Я–ї–∞–љ —Е—А–∞–Љ–Њ–≤–Њ–≥–Њ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–∞ –Я—А—Н–∞—Е–≤–Є—Е–µ–∞ –Ь–µ–і–Є–∞—Д–∞–є–ї—Л –љ–∞ –Т–Є–Ї–Є—Б–Їпњљ...

Song performed by Kelly Clarkson Save YouSong by Kelly Clarksonfrom the album All I Ever Wanted Recorded2008Studio Henson Recording, Los Angeles Mansfield, Los Angeles Ocean Way, Nashville Blackbird, Nashville GenreRock[1]Length4:03LabelRCASongwriter(s)Ryan Tedder, Aimée ProalProducer(s)Ryan Tedder Save You is a song by American recording artist Kelly Clarkson, from her fourth studio album, All I Ever Wanted (2009). Written by Ryan Tedder and Aimée Proal, and produced by Tedder, Sav...
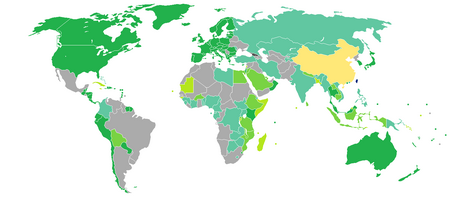
жПРз§ЇпЉЪж≠§жЭ°зЫЃй°µзЪДдЄїйҐШдЄНжШѓдЄ≠еЬЛвАФзСЮе£ЂйЧЬдњВгАВ йЧЬжЦЉдЄ≠иПѓж∞СеЬЛиИЗгАМзСЮгАНе≠ЧеЬЛеЃґзЪДе§ЦдЇ§йЧЬдњВпЉМи©≥и¶ЛдЄ≠зСЮйЧЬдњВ (жґИж≠ІзЊ©)гАВ дЄ≠иПѓж∞СеЬЛвАФзСЮе£ЂйЧЬдњВ дЄ≠иПѓж∞СеЬЛ зСЮе£Ђ дї£и°®ж©ЯжІЛйІРзСЮе£ЂеП∞еМЧжЦЗеМЦзґУжњЯдї£и°®еЬШзСЮе£ЂеХЖеЛЩиЊ¶дЇЛиЩХдї£и°®дї£и°® йїГеБЙе≥∞ е§Ідљњ[и®ї 1][4]иЩХйХЈ йЩґжЦєе©≠[5]Mrs. Claudia Fontana Tobiassen дЄ≠иПѓж∞СеЬЛвАФзСЮе£ЂйЧЬдњВпЉИеЊЈи™ЮпЉЪSchweizerischeвАУrepublik china BeziehungenгАБж≥Хпњљ...

–І–∞—Б—В–Є–љ–∞ —Б–µ—А—Ц—Ч –њ—А–Њ–§—Ц–ї–Њ—Б–Њ—Д—Ц—ПLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, Averroes–Я–ї–∞—В–Њ–љ–Ъ–∞–љ—В–Э—Ц—Ж—И–µ–С—Г–і–і–∞–Ъ–Њ–љ—Д—Г—Ж—Ц–є–Р–≤–µ—А—А–Њ–µ—Б –§—Ц–ї–Њ—Б–Њ—Д–Є –Х–њ—Ц—Б—В–µ–Љ–Њ–ї–Њ–≥–Є –Х—Б—В–µ—В–Є–Ї–Є –Х—В–Є–Ї–Є –Ы–Њ–≥—Ц–Ї–Є –Ь–µ—В–∞—Д—Ц–Ј–Є–Ї–Є –°–Њ—Ж—Ц–∞–ї—М–љ–Њ-–њ–Њ–ї—Ц—В–Є—З–љ—Ц —Д—Ц–ї–Њ—Б–Њ—Д–Є –Ґ—А–∞–і–Є—Ж—Ц—Ч –Р–љ–∞–ї—Ц—В–Є—З–љ–∞ –Р—А—Ц—Б—В–Њ—В–µ–ї—Ц–≤—Б—М–Ї–∞ –Р—Д—А–Є–Ї–∞–љ—Б—М–Ї–∞ –С–ї–Є–Ј—М–Ї–Њ—Б—Е—Ц–і–љ–∞ —Ц—А–∞–љ—Б—М–Ї–∞ –С—Г–і–і—Ц–єпњљ...

Islamic organisation based in Pakistan Dawat-e-IslamiЎѓЎєўИЎ™ўР ЎІЎ≥ўДЎІўЕџМTotal population30 to 40 millionFounderIlyas Qadri[1]ReligionsIslamScripturesQuranHadithSunnatLanguagesLiturgical: ArabicIn India and Pakistan: UrduIn the diaspora:In the UK: Respective regional languagesWebsitewww.dawateislami.net Dawat-e-Islami (Urdu: ЎѓЎєўИЎ™ўР ЎІЎ≥ўДЎІўЕџМ) is a Sunni Islamic organization based in Pakistan. It has several Islamic educational institutions around the world. In addition to l...

United States naval base on the island of Oahu, Hawaii Naval Station Pearl Harbor Part of Navy Region HawaiiOahu, Hawaii Naval Station Pearl HarborCoordinates21¬∞20вА≤57вА≥N 157¬∞56вА≤38вА≥W / 21.349270¬∞N 157.943970¬∞W / 21.349270; -157.943970TypeMilitary baseSite informationControlled byUnited States NavySite historyIn use1899вАУpresent United States historic placePearl Harbor, U.S. Naval BaseU.S. National Register of Historic PlacesU.S. National Historic L...

жШОжЬЭеЕ≥и•њеЕЂеНЂ 赧жЦ§иТЩеП§еНЂпЉМжШОжЬЭеЕ≥и•њеЕЂеНЂдєЛдЄАпЉМзЃАзІ∞赧жЦ§еНЂпЉМеПИдљЬ赧йЗСеНЂгАВ жШОжЬЭ жШОжЬЭж∞ЄдєРдЇМеєіпЉИ1404еєіпЉЙеЕГжЬЭдЄЮзЫЄиЛ¶жЬѓдєЛе≠Ре°ФеКЫе∞ЉжКХйЩНжШОжЬЭпЉМдї•еЕґжЙАйГ®еܮ赧жЦ§зЂЩ职皁赧жЦ§иТЩеП§еНГжИЈжЙАпЉМеЬ®дїКзФШиВГзЬБзОЙйЧ®еЄВи•њеМЧ赧йЗСе†°гАВж∞ЄдєРеЕЂеєіпЉИ1410еєіпЉЙеНЗ䪯赧жЦ§еНЂпЉМж≠£еЊЈеєій׳襀еРРй≤БзХ™ж±ЧеЫљжЙАз†іпЉМељУеЬ∞дЇЇеЖЕеЊЩиВГеЈЮзЪДеНЧе±±пЉМ赧жЦ§еЯОз©ЇгАВ жЄЕжЬЭ жЄЕеЬ£з•ЦеЇЈзЖЩдЇФеНБдЄГеєіпЉИ1718еєіпЉЙпЉМжБҐе§Н赧йЗСеНЂпЉМжЄЕдЄЦеЃЧйЫНж≠£...

ЎІўДЎєўДЎІўВЎІЎ™ ЎІўДўЖўКЎђўКЎ±ўКЎ© ЎІўДўЖўКўГЎІЎ±ЎІЎЇўИўКЎ© ўЖўКЎђўКЎ±ўКЎІ ўЖўКўГЎІЎ±ЎІЎЇўИЎІ ўЖўКЎђўКЎ±ўКЎІ ўЖўКўГЎІЎ±ЎІЎЇўИЎІ Ў™ЎєЎѓўКўД ўЕЎµЎѓЎ±ўК - Ў™ЎєЎѓўКўД ЎІўДЎєўДЎІўВЎІЎ™ ЎІўДўЖўКЎђўКЎ±ўКЎ© ЎІўДўЖўКўГЎІЎ±ЎІЎЇўИўКЎ© ўЗўК ЎІўДЎєўДЎІўВЎІЎ™ ЎІўДЎЂўЖЎІЎ¶ўКЎ© ЎІўДЎ™ўК Ў™ЎђўЕЎє Ў®ўКўЖ ўЖўКЎђўКЎ±ўКЎІ ўИўЖўКўГЎІЎ±ЎІЎЇўИЎІ.[1][2][3][4][5] ўЕўВЎІЎ±ўЖЎ© Ў®ўКўЖ ЎІўДЎ®ўДЎѓўКўЖ ўЗЎ∞ўЗ ўЕўВЎІЎ±ўЖЎ© ЎєЎІўЕЎ© ўИўЕЎ±ЎђЎєўКЎ© ўДўДпњљ...

2014 European Rowing ChampionshipsLocationBelgrade, SerbiaDates30 May вАУ 1 June 2014← 2013 Seville2015 Pozna≈Д → The 2014 European Rowing Championships was held in Belgrade, Serbia, between 30 May and 1 June 2014. Medal summary Men Event Gold Time Silver Time Bronze Time LM1x[1] Pedro Fraga (POR) 6:51.72 Marcello Miani (ITA) 6:54.42 Michael Schmid (SUI) 6:56.44 M1x[2] Ond≈Щej Synek (CZE) 6:54.95 Marcel H...

Football stadium in Rafaela, Argentina This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Estadio Parque Barrio Ilolay вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (January 2021) (Learn how and when to remove this message) Estadio-parque-bh.JPG Estadio Parque Barrio Ilolay is a multi-use stadium in Rafaela, Ar...

–Т –Т–Є–Ї–Є–њ–µ–і–Є–Є —Б—Г—Й–µ—Б—В–≤—Г—О—В —Б—В–∞—В—М–Є –Њ –і—А—Г–≥–Є—Е –ї—О–і—П—Е —Б –Є–Љ–µ–љ–µ–Љ –°–µ—А–∞—Д–Є–Љ –Є —Д–∞–Љ–Є–ї–Є–µ–є –°–Њ–±–Њ–ї–µ–≤. –Р—А—Е–Є–µ–њ–Є—Б–Ї–Њ–њ –°–µ—А–∞—Д–Є–Љ –Р—А—Е–Є–µ–њ–Є—Б–Ї–Њ–њ –С–Њ–≥—Г—З–∞—А—Б–Ї–Є–є, –≤–Є–Ї–∞—А–Є–є –Т–Њ—А–Њ–љ–µ–ґ—Б–Ї–Њ–є –µ–њ–∞—А—Е–Є–Є –∞–њ—А–µ–ї—М 1921 вАФ 1920-–µ –¶–µ—А–Ї–Њ–≤—М –†—Г—Б—Б–Ї–∞—П –њ—А–∞–≤–Њ—Б–ї–∞–≤–љ–∞—П —Ж–µ—А–Ї–Њ–≤—М, –†—Г—Б—Б–Ї–∞—П –њ—А–∞–≤–Њ—Б–ї–∞–≤–љ–∞—П —Ж–µ—А–Ї–Њ–≤—М –Ј–∞–≥—А–∞–љ–Є—Ж–µ–є –Я—А–µ–µ–Љ–љ–Є–Ї –Т–їпњљ...











