Линейная древесность
|
Read other articles:

Independent school in Flowood, Mississippi, United StatesJackson Preparatory SchoolAddress3100 Lakeland DriveFlowood, MississippiUnited StatesCoordinates32°19′59″N 90°6′30″W / 32.33306°N 90.10833°W / 32.33306; -90.10833InformationTypeIndependentMottoScholarship, Service, Character, LeadershipEstablished1970FounderDr. Marshall FortenberryHeadmasterLawrence CocoGradesPre-k through 12GenderCoeducationalCampus size84 acres (34 ha)Color(s)Blue and RedAthlet...

1964–65 in Scottish footballDivision One championsKilmarnockDivision Two championsStirling AlbionScottish Cup winnersCelticLeague Cup winnersRangersJunior Cup winnersLinlithgow RoseTeams in EuropeCeltic, Dundee, Dunfermline Athletic, Kilmarnock, RangersScotland national team1965 BHC, 1966 World Cup qualification The 1964–65 season was the 92nd season of competitive football in Scotland and the 68th season of Scottish league football.[1] Scottish League Division One Main article: ...

Model kapal Trireme Yunani Kapal perang layar adalah kapal perang masa lampau yang tenaga penggeraknya dengan bantuan angin dan layar. lazim digunakan pada masa lampau pada abad abad tumbuhnya peradaban, abad pertengahan, perdagangan, sampai abad penjelajahan. Tercatat pertempuran-pertempuran terjadi pada masa lampau di antaranya perang laut antara armada Romawi dan Karthago, pertempuran Lepanto, pertempuran laut Inggris-Spanyol serta pertempuran Trafalgar. Pada awalnya, kapal perang yang dig...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Mangkunegara Xꦩꦁꦏꦸꦤꦒꦫ꧇꧑꧐꧇Kanjeng Gusti Pangeran Adipati AryoAdipati Mangkunegaran ke-10Berkuasa12 Maret 2022 – sekarangPenobatan12 Maret 2022PendahuluMangkunegara IXPresidenJoko WidodoInformasi pribadiKelahiranGusti Pangeran Haryo Bhre Cakrahutomo Wira Sudjiwo29 Maret 1997 (umur 27)WangsaWa...

Unicameral legislature and representative body of Albania Parliament of Albania Kuvendi i Shqipërisë31st LegislatureTypeTypeUnicameral Term limitsFour yearsHistoryFounded27 March 1920; 104 years ago (1920-03-27)LeadershipSpeakerLindita Nikolla, PS since 10 September 2023 (2023-09-10) Majority parliamentary group leaderBledar Çuçi, PS since 26 July 2023 (2023-07-26) Minority parliamentary group leaderDisputed, PD[a] since ...

Supertall skyscraper in Wenzhou, Zhejiang, China Wenzhou World Trade CenterGeneral informationStatusCompletedTypeMixed-useLocationWenzhou, Zhejiang, ChinaCoordinates28°00′25″N 120°39′54″E / 28.006896°N 120.664993°E / 28.006896; 120.664993Construction startedJune 9, 2003CompletedApril 18, 2010OpeningOctober 20, 2010HeightArchitectural321.9 m (1,056 ft)[1]Technical detailsFloor count68[1]Floor area174,361 m2 (1,876,806 sq&#...

Johann Petrejus, illustration du Livre II du De Architectura de Vitruve, par Walther Hermann Ryff, 1547. Une définition de l'histoire de la construction, qui la distingue de l'histoire de l'architecture, pourrait nous être donnée par Vitruve : elle s'attache à décrire les matériaux que fournit la nature et l'usage qu'on en fait. Il n'y est pas question de l'origine de l'architecture, mais bien de celle des bâtiments, ainsi que de la manière dont on est parvenu à donner à l'art ...

Cet article est une ébauche concernant le Canada. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Commissaire des Territoires du Nord-Ouest(en) Commissioner of the Northwest Territories Armoiries du commissairedes Territoires du Nord-Ouest. Drapeau du commissaire. Titulaire actuelleMargaret Thomdepuis le 18 septembre 2017 Création 24 août 1905 Titre L'honorable Mandant Gouverneur général du Canada Premier t...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (septembre 2010). Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes. Flux migratoire des Bretons au VIe siècle,...
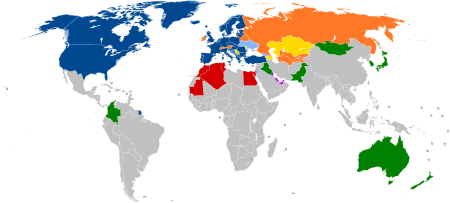
NATO initiative in West Asia Member states of the ICI. The Istanbul Cooperation Initiative (ICI) is a NATO initiative that was launched during the organisation's 2004 Istanbul summit. During the summit, NATO leaders decided to elevate[clarification needed] the Alliance's Mediterranean Dialogue to a genuine partnership and to launch the ICI with selected countries in West Asia.[1] The initiative is an offer to engage in practical security cooperation activities with states thro...

1988 single by Morrissey This article is about the song. For the subculture, see Suedehead (subculture). For the album, see Suedehead: The Best of Morrissey. SuedeheadSingle by Morrisseyfrom the album Viva Hate B-side I Know Very Well How I Got My Name Hairdresser on Fire Oh Well, I'll Never Learn Released15 February 1988 (1988-02-15)[1]GenreJangle pop[2]Length3:54LabelHMVSongwriter(s) Morrissey Stephen Street Producer(s)Stephen StreetMorrissey singles chronolog...

Chinese manufacturer owned by Changan Automobile Changan OshanFormerlyChangan Commercial Vehicles (2010-2017)Company typeState-ownedIndustryAutomotiveFounded2010Defunct2024FateMerged into Changan brandHeadquartersChongqing, ChinaArea servedWorldwideProductsMotor vehiclesWebsitehttps://www.oshanauto.com/ Oshan (Chinese: 欧尚; pinyin: Ōushàng) was a passenger car brand under Changan Automobile. It was originally known as the Changan Commercial Vehicles, the division which focuses pr...

Capital city of Jilin Province, China For other uses, see Changchun (disambiguation). Prefecture-level & Sub-provincial city in Jilin, ChinaChangchun 长春市Prefecture-level & Sub-provincial cityClockwise from top: panoramic view from Shengtai Plaza, panoramic view of Ji Tower, Former Manchukuo State Department, Statue on cultural square, Changchun Christian Church, Soviet martyr monument.Nickname: 北国春城 (Spring City of the Northern Country)Location of Changchun City (ye...

Practitioner of accounting or accountancy This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Accountant – news · newspapers · books · scholar · JSTOR (September 2015) (Learn how and when to remove this message) OccupationNamesCertified Public Accountant (Accounts Officer), Chartered Certified Accountants, Chart...

Mechanical apparatus used to send messages For other uses, see Semaphore (disambiguation). Coastal semaphore using moving arms at Scheveningen, circa 1799 Semaphore (lit. 'apparatus for signalling'; from Ancient Greek σῆμα (sêma) 'mark, sign, token', and Greek -φόρος (-phóros) 'bearer, carrier')[1] is the use of an apparatus to create a visual signal transmitted over distance.[2][3] A semaphore can be performed with dev...

جمهورية الدومينيكان (بالإسبانية: República Dominicana) جمهورية الدومينيكانعلم جمهورية الدومينيكان جمهورية الدومينيكانشعار جمهورية الدومينيكان الشعار الوطني(بالإسبانية: Dios, Patria, Libertad) النشيد: نشيد جمهورية الدومينيكان الوطني الأرض والسكان إحداثيات 18°48�...

American teen sitcom This article is about the Nickelodeon television series. For other uses, see Victorious (disambiguation). VictoriousGenreTeen sitcomCreated byDan SchneiderShowrunnerDan SchneiderStarring Victoria Justice Leon Thomas III Matt Bennett Elizabeth Gillies Ariana Grande Avan Jogia Daniella Monet Theme music composer Łukasz Gottwald Michael Corcoran Dan Schneider Opening themeMake It Shine, performed by Victoria JusticeCountry of originUnited StatesOriginal languageEnglishNo. o...

Disambiguazione – Se stai cercando altri significati, vedi Lodi (disambigua). Lodicomune (dettagli) (dettagli) Lodi – VedutaPiazza della Vittoria LocalizzazioneStato Italia Regione Lombardia Provincia Lodi AmministrazioneSindacoAndrea Furegato (PD) dal 15-6-2022[1] TerritorioCoordinate45°19′N 9°30′E45°19′N, 9°30′E (Lodi) Altitudine87 m s.l.m. Superficie41,38 km² Abitanti45 212[2] (28-2-2024) Densità1 092,61...

Untuk planet ini dinamai setelah Dewa Romawi ini, lihat Mars. MarsDewa Perang dan AgrikulturPatung Mars dari Forum Nerva, abad ke-2 M, berdasarkan karya asli era Augustus yang pada gilirannya menggunakan model Yunani Helenistik dari abad ke-4 SM. Museum Capitolini di Roma, Italia.[1]Nama lainMavors, Mavorte (kuno, puitis)PlanetMarsSimbolTombak Mars ♂ (Ikon tombak dan tameng)HariSelasaInformasi pribadiNerio dan lainnya Rhea Silvia (raped), Venus, BellonaAnakRomulus dan Remus, CupidOr...

Pour les articles homonymes, voir Bagdad (homonymie). Cet article possède un paronyme, voir Bagad. Bagdad (ar) بَغْدَاد Héraldique Drapeau De haut en bas et de gauche à droite :tour de l'horloge d'al-Qushla, cathédrale Saint-Joseph, mains de la victoire et mosquée al-Khulafa ;porte assyrienne du musée national d'Irak ;mausolée d'Omar Sohrawardi et sanctuaire al-Kadhimiya. Administration Pays Irak Province Bagdad Maire Alaa Maan Démographie Gentilé Bagdadien[1]...






