Крус, Вальтер

В Википедии есть статьи о других людях с фамилией Крус.
Шахматы
Вальтер Крус
Walter Cruz
Страны  Бразилия
Дата рождения 23 января 1910(1910-01-23)
Место рождения Петрополис
Дата смерти 3 января 1967(1967-01-03) (56 лет)
Место смерти Рио-де-Жанейро

Вальтер Освальдо Крус (порт. Walter Oswaldo Cruz, 23 января 1910, Петрополис — 3 января 1967, Рио-де-Жанейро) — бразильский шахматист, национальный мастер.

Чемпион Бразилии 1938, 1940, 1942, 1948, 1949 и 1953 гг. (в 1942 г. сохранил звание, добившись ничьей в матче с П. Дуарте). Вице-чемпион Бразилии 1928, 1929 и 1939 гг. (в 1928 и 1929 гг. проиграл матчи за титул Ж. Соузе Мендешу, в 1939 г. — О. Тромповскому).

В составе сборной Бразилии участник официальной и неофициальной шахматных олимпиад.

Участник ряда крупных турниров на территории Северной и Южной Америки, в том числе чемпионата Южной Америки 1928 г. и зональных турниров 1954 и 1957 гг.

В 1939 г. вместе со своим старшим братом О. Крусом, О. Тромповским, Р. Шарлиером и А. Силвой Рошей участвовал в показательных выступлениях чемпиона мира А. А. Алехина в Рио-де-Жанейро.[1]

По специальности — врач-гематолог. Возглавлял Институт Освальдо Круса (эпидемиологический центр) в Рио-де-Жанейро. Институт назван именем его отца Освальдо Круса-старшего, известного эпидемиолога, бактериолога и гигиениста.

Спортивные результаты

Год Город Соревнование + − = Результат Место
1928 Мар-дель-Плата Чемпионат Южной Америки 6 6 4 8 из 16 9[2]
Рио-де-Жанейро Матч с Ж. Соузой Мендешем (на звание чемпиона Бразилии) Матч проигран
1929 Рио-де-Жанейро Матч с Ж. Соузой Мендешем (на звание чемпиона Бразилии) Матч проигран
1936 Мюнхен Неофициальная шахматная олимпиада (сборная Бразилии, 3-я доска) 3 9 8 7 из 20[3]
1938 Рио-де-Жанейро Матч с О. Тромповским (на звание чемпиона Бразилии) Матч выигран
Монтевидео Международный турнир 4 3 8 8 из 15 7[4]
1939 Рио-де-Жанейро Матч с О. Тромповским (на звание чемпиона Бразилии) 2 5 1 2½ : 5½
Буэнос-Айрес VIII Олимпиада (сборная Бразилии, 3-я доска) 4 7 5 6½ из 16
1940 Рио-де-Жанейро Чемпионат Бразилии (отборочный турнир) 5½ из 8 1[5]
Рио-де-Жанейро Матч с О. Тромповским (на звание чемпиона Бразилии) 5 1 1 5½ : 1½
Гамильтон Чемпионат Шахматной ассоциации штата Нью-Йорк 4
1941 Гамильтон Чемпионат Шахматной ассоциации штата Нью-Йорк 7—8[6]
1942 Сан-Паулу Матч с П. Дуарте (на звание чемпиона Бразилии) 5 : 5
1943 Рио-де-Жанейро Международный турнир 3—4[7]
Рио-де-Жанейро Турнир четырех шахматистов 3[7]
1945 Голливуд Панамериканский чемпионат 2 4 6 5 из 12 9—10[8]
1946 Рио-де-Жанейро Турнир памяти А. А. Алехина 3[7]
Рио-де-Жанейро Международный турнир 3[9]
1947 Мар-дель-Плата Международный турнир 2 8 7 5½ из 17 15[9]
Рио-де-Жанейро Международный турнир 3
1948 Рио-де-Жанейро Чемпионат Бразилии 1
Рио-де-Жанейро Международный турнир 3
1949 Рио-де-Жанейро Чемпионат Бразилии 1
Мар-дель-Плата Международный турнир 3 5 9 7½ из 17 11—13[10]
1952 Рио-де-Жанейро Международный турнир 3 8 5 5½ из 16 12—13[10]
1953 Рио-де-Жанейро Чемпионат Бразилии 1
1954 Мар-дель-Плата Зональный турнир 6 9 6 9 из 21 13[11]
1957 Рио-де-Жанейро Зональный турнир 1 10 4 3 из 15 16[11]

Примечания

  1. ↑ Чарушин В. А. 226 коротких партий Александра Алехина. — Н. Новгород: Автозаводец-книга, 1992. — С. 110—112.
  2. ↑ Победил Р. Грау.
  3. ↑ В базах есть победа над М. Монтичелли (Италия) и ничья с А. Цветковым (Болгария).
  4. ↑ Победил А. А. Алехин.
  5. ↑ 5 участников играли в 2 круга.
  6. ↑ Победил Р. Файн.
  7. ↑ 1 2 3 Победил Э. Элисказес.
  8. ↑ Победил С. Решевский.
  9. ↑ 1 2 Победил М. Найдорф.
  10. ↑ 1 2 Победил Э. Россетто.
  11. ↑ 1 2 Победил О. Панно.

Ссылки

Read other articles:

Maia (grup musik)

MAIAAsalJakarta, IndonesiaGenrePopTahun aktif2008–sekarangLabelSony Music Entertainment Indonesia (2008–2011)Le Moesiek (2012–sekarang)Situs webwww.duniamaia.comAnggotaMaia EstiantyMantan anggotaMey Chan MAIA (juga dikenal sebagai DuoMaia) adalah sebuah grup duet yang dibentuk pada tahun 2008 dan awalnya beranggotakan Maia Estianty dan Mey Chan. Pada tahun 2018, Mey Chan mengundurkan diri karena ingin fokus dengan keluarga dan berkarier solo. Sejak itu belum ditemukan penggantinya oleh ...

 

 

Photographic lens design

Design of lenses for use in cameras For general lens design, see Optical lens design. The design of photographic lenses for use in still or cine cameras is intended to produce a lens that yields the most acceptable rendition of the subject being photographed within a range of constraints that include cost, weight and materials. For many other optical devices such as telescopes, microscopes and theodolites where the visual image is observed but often not recorded the design can often be signif...

 

 

Longkeyang, Bodeh, Pemalang

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Longkeyang, Bodeh, Pemalang – berita · surat kabar · buku · cendekiawan · JSTOR Artikel atau bagian mungkin perlu ditulis ulang agar sesuai dengan standar kualitas Wikipedia. Anda dapat membantu memperba...

Address space

Computing concept In computing, an address space defines a range of discrete addresses, each of which may correspond to a network host, peripheral device, disk sector, a memory cell or other logical or physical entity. For software programs to save and retrieve stored data, each datum must have an address where it can be located. The number of address spaces available depends on the underlying address structure, which is usually limited by the computer architecture being used. Often an addres...

 

 

Concordia, Entre Ríos

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2012) (Learn how and when to remove this message) City in Entre Ríos, ArgentinaConcordiaCityConcordiaLocation of Concordia in ArgentinaCoordinates: 31°24′S 58°2′W / 31.400°S 58.033°W / -31.400; -58.033Country ArgentinaProvinceEntre RíosDepartmentConcordiaFoundedNovemb...

 

 

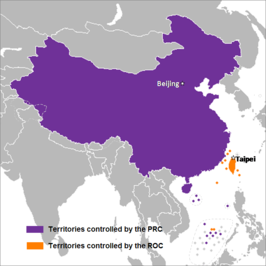
Dua Tiongkok

Dua Tiongkok Wilayah yang dikuasai oleh Republik Rakyat Tiongkok (RRT) (ungu) dan Republik Tiongkok (Taiwan) (oranye). Ukuran pulau kecil telah diperbesar dalam peta ini untuk kemudahan identifikasi. Hanzi tradisional: 兩個中國 Hanzi sederhana: 两个中国 Alih aksara Mandarin - Hanyu Pinyin: liǎng gè Zhōngguóliǎng ge Zhōngguó - Wade-Giles: liang3 ge4 zhong1 guo2 - Romanisasi Yale: LyangGeJungGwo - Bopomofo: ㄌㄧㄤˇ ㄍㄜ` ㄓㄨㄥ ㄍㄨㄛ´ Dua Tiongkok mengacu kepada si...

Campeonato de Portugal 1925

Campeonato de Portugal 1925Campeonato de Portugal 1925 Competizione Taça de Portugal Sport Calcio Edizione 4ª Date dal 31 maggio 1925al 28 giugno 1925 Luogo  Portogallo Sede finale Campo de Monserrate Risultati Vincitore  Porto(2º titolo) Secondo  Sporting Lisbona Semi-finalisti  Olhanense Espinho Statistiche Incontri disputati 8 Gol segnati 39 (4,88 per incontro) Cronologia della competizione 1924 1926 Manuale Il Campeonato de Portugal 1925 fu la qua...

 

 

密西西比州

此條目可参照英語維基百科相應條目来扩充。 (2017年8月)若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。 密西西比州 美國联邦州State of Mississippi 州旗州徽綽號：木蘭之州地图中高亮部分为密西西比州坐标：30°13'N�...

 

 

St. Josaphat Roman Catholic Church (Chicago)

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: St. Josaphat Roman Catholic Church Chicago – news · newspapers · books · scholar · JSTOR (October 2013) (Learn how and when to remove this message) Church in Chicago, United StatesSt. JosaphatChurchSt. JosaphatChurch41°55′25.1″N 87°39′46.8″Wþ...

约翰斯顿环礁

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题，请协助参考外语维基百科扩充条目。请勿直接提交机械翻译，也不要翻译不可靠、低品质内容。依版权协议，译文需在编辑摘要注明来源，或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌：《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

 

 

Філософія

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

 

 

Ashmore and Cartier Islands

External territory of Australia in the Indian Ocean Territory of Ashmore and Cartier IslandsLocation of the Ashmore and Cartier IslandsGeographyLocationIndian OceanCoordinates12°15′30″S 123°02′30″E / 12.25833°S 123.04167°E / -12.25833; 123.04167Major islands4Administration AustraliaDemographicsPopulation0 (July 2021) Satellite image of Ashmore reef on 26 August 2021. The Territory of Ashmore and Cartier Islands[1] is an uninhabited Australian e...

Одесса

У этого термина существуют и другие значения, см. Одесса (значения). ГородОдессаукр. Одеса Против часовой стрелки, начиная с верхнего правого угла: памятник дюку де Ришельё, Воронцовский маяк, городской сад, театр оперы и балета, Приморский бульвар, Потёмкинская лестница Ф...

 

 

Andrew Barclay Sons & Co.

UK locomotive manufacturer Andrew Barclay Sons & Co.Operating as Wabtec Rail ScotlandTraded asBrodie EngineeringIndustryEngineeringPredecessorBarclays & Co.Founded1892FounderAndrew BarclaySuccessorHunslet-Barclay (1972-2007)Brush-Barclay (2007-2011)Wabtec Rail Scotland (2011-2020)Brodie Engineering Ltd (2020–present)HeadquartersWest Langland Street, Kilmarnock, ScotlandArea servedScotlandProductsLocomotivesServicesLocomotive repairs and maintenanceOwnerBrodie Engineering Ltd.Website...

 

 

Logical positivism

Movement in Western philosophy Part of a series onPhilosophy Philosophy portal Contents Outline Lists Glossary History Categories Philosophies By period Ancient Ancient Egyptian Ancient Greek Medieval Renaissance Modern Contemporary Analytic Continental By region African Egypt Ethiopia South Africa Eastern philosophy Chinese Indian Indonesia Japan Korea Vietnam Indigenous American Aztec philosophy Middle Eastern philosophy Iranian Western American British French German Italian Russian By ...

Westham, Dorset

Place in Dorset, UK Human settlement in EnglandWesthamWestham BridgeWesthamLocation within DorsetCivil parishWeymouthUnitary authorityDorsetShire countyDorsetRegionSouth WestCountryEnglandSovereign stateUnited KingdomPost townWeymouthPostcode districtDT4PoliceDorsetFireDorset and WiltshireAmbulanceSouth Western UK ParliamentSouth Dorset List of places UK England Dorset 50°36′43″N 2°28′12″W / 50.61194°N 2.47000°W / 50.61194; -2.47000...

 

 

Patricia Cornwell

Patricia Cornwell Patricia Cornwell lahir pada tanggal 9 Juni 1956. Kota kelahirannya adalah Miami, yang terletak di negara bagian Florida, Amerika Serikat. Cornwell merupakan penulis novel dengan genre kejahatan hukum.[1] Patricia menulis novel-novel terkenal dengan seorang tokoh bernama Scarpetta pada tahun 1984 hingga tahun 1988. Novel-novel karya Patricia telah diterjemahkan ke berbagai bahasa dan terjual laris di berbagai negara.[2] Keluarga Nama asli dari Patricia Cornwe...

 

 

Amanattō

Japanese traditional confectionery AmanattōPeanut amanattōTypeConfectioneryPlace of originJapanRegion or stateEast AsiaCreated byHosoda YasubeiMain ingredientsAdzuki or other beans, sugar, sugar syrup Amanattō (甘納豆) is a Japanese traditional confectionery made of azuki or other beans, covered with refined sugar after simmering with sugar syrup and drying.[1] It was developed by Hosoda Yasubei during the Bunkyū years (1861–1863) in the Edo period. He opened a wagashi store ...

Sentience

Déterminer quels animaux peuvent éprouver des sensations est difficile, mais les scientifiques s'accordent généralement à dire que les vertébrés, ainsi que certaines espèces d'invertébrés, sont probablement sentients[1],[2]. La sentience (du latin sentiens, de sentire « percevoir par les sens ») désigne la capacité d'éprouver des choses subjectivement, d'avoir des expériences vécues. Les philosophes du XVIIIe siècle utilisaient ce concept pour distinguer la ca...

 

 

German reunification

1989–1991 unification process of Germany with its full sovereignty returned For the unification of most German states in the 1800s, see Unification of Germany. Reunification of GermanyPart of the Revolutions of 1989 and the end of the Cold WarGermans stand on top of the Wall in front of the Brandenburg Gate in the days before the Wall was torn down.Native name Deutsche WiedervereinigungDie WendeDate9 November 1989 – 15 March 1991 (1989-11-09 – 199...