–ö–Ľ–Ķ—ā–ļ–į (—ā–Ķ–ĺ—Ä–ł—Ź –≥—Ä–į—Ą–ĺ–≤)
|
Read other articles:
Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak men...

Country Garden Holdings Company Limited ÁĘßś°āŚõ≠śéߍā°śúČťôźŚÖ¨ŚŹłJenisPerusahaan publikKode emitenSEHK: 2007IndustriLahan yasan, pendidikanDidirikan1992PendiriYang GuoqiangKantorpusatShunde, Guangdong, TiongkokWilayah operasiTiongkok, Malaysia,[1] Australia[2]TokohkunciKetua: Yang GuoqiangPemegang saham terbesar: Yang HuiyanProdukPerumahan, komersial, rekreasi dan perhotelanJasaManajemen properti dan fasilitas, manajemen hotel, sekolahPendapatanUS$33,8 miliar (2018...

Panci dari tembaga dengan telinga pada sisinya. Panci (bahasa Inggris: saucepan) adalah alat masak yang terbuat dari logam (alumunium, baja, dll) dan berbentuk silinder atau mengecil pada bagian bawahnya. Panci bisa memiliki gagang tunggal atau dua telinga pada kedua sisinya, gagang atau telinga ini difungsikan sebagai pegangan untuk membawa ataupun mengangkat panci dan biasanya digunakan untuk memasak air, sayur berkuah, dll. Ukuran panci biasanya dinyatakan dengan volumenya (biasanya antara...

ōßŔĄōĻŔĄōßŔāōßō™ ōßŔĄō•ŔÖōßōĪōßō™Ŕäō© ōßŔĄōĻōĪōßŔāŔäō© ōßŔĄōĻōĪōßŔā ōßŔĄō•ŔÖōßōĪōßō™ ōßŔĄō≥ŔĀōßōĪōßō™ ō≥ŔĀōßōĪō© ōßŔĄō£ŔÖōßōĪōßō™ ŔĀŔä ō®ōļōĮōßōĮ ōßŔĄō≥ŔĀŔäōĪ : ō≠ō≥ŔÜ ō£ō≠ŔÖōĮ ōßŔĄōīō≠Ŕä ōßŔĄōĻŔÜŔąōßŔÜ : ō®ōļōĮōßōĮ ŔÖō¨ŔÖōĻ ōßŔĄō≥ŔĀōßōĪōßō™ -ōßŔĄŔÖŔÜō∑Ŕāō© ōßŔĄōģō∂ōĪōßō° ō≥ŔĀōßōĪō© ōßŔĄōĻōĪōßŔā ŔĀŔä ō£ō®Ŕąōłō®Ŕä ōßŔĄō≥ŔĀŔäōĪ : ōĻō®ōĮ ōßŔĄŔĄŔá ōßŔĄōĘŔĄŔąō≥Ŕä ōßŔĄōĻŔÜŔąōßŔÜ : ō£ō®Ŕąōłō®Ŕä ŔÖŔÜō∑Ŕāō© ōß...

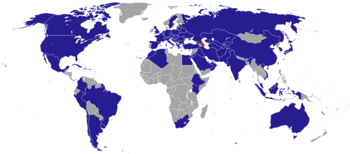
Duta Besar Amerika Serikat untuk YugoslaviaSegel Kementerian Dalam Negeri Amerika SerikatDicalonkan olehPresiden Amerika SerikatDitunjuk olehPresiden Berikut ini adalah daftar Duta Besar Amerika Serikat untuk Yugoslavia Daftar Henry Percival Dodge John Dyneley Prince Charles S. Wilson Arthur Bliss Lane Anthony J. Drexel Biddle, Jr. Lincoln MacVeagh Richard C. Patterson, Jr. Cavendish W. Cannon George V. Allen James Williams Riddleberger Karl L. Rankin George F. Kennan Charles Burke Elbrick Wi...

Town in New Hampshire, United StatesWalpole, New HampshireTownTown Hall in 2019Location in Cheshire County, New HampshireCoordinates: 43¬į04‚Ä≤46‚Ä≥N 72¬į25‚Ä≤33‚Ä≥W / 43.07944¬įN 72.42583¬įW / 43.07944; -72.42583CountryUnited StatesStateNew HampshireCountyCheshireIncorporated1756Named forRobert WalpoleVillagesWalpoleNorth WalpoleDrewsvilleGovernment ‚ÄĘ SelectboardPeggy Pschirrer, ChairSteve DalessioCheryl MayberryArea[1] ‚ÄĘ Total36....

ō≥ō™ŔäŔĀōßŔÜ ŔĄōßŔÜŔąŔä (ō®ōßŔĄŔĀōĪŔÜō≥Ŕäō©: St√©phane Lannoy)‚ÄŹ ŔÖōĻŔĄŔąŔÖōßō™ ōīōģōĶŔäō© ōßŔĄŔÖŔäŔĄōßōĮ 18 ō≥ō®ō™ŔÖō®ōĪ 1969 (ōßŔĄōĻŔÖōĪ 54 ō≥ŔÜō©)ō®ŔąŔĄŔąŔÜŔä ō≥ŔąōĪ ŔÖŔäōĪ ōßŔĄō∑ŔąŔĄ 185 ō≥ŔÜō™ŔäŔÖō™ōĪ ōßŔĄō¨ŔÜō≥Ŕäō© ŔĀōĪŔÜō≥ōß ō™ōĻōĮŔäŔĄ ŔÖōĶōĮōĪŔä - ō™ōĻōĮŔäŔĄ ō≥ō™ŔäŔĀōßŔÜ ŔĄōßŔÜŔąŔä (ō®ōßŔĄŔĀōĪŔÜō≥Ŕäō©: St√©phane Lannoy)‚ÄŹōĆ ŔÖŔÜ ŔÖŔąōßŔĄŔäōĮ 18 ō≥ō®ō™ŔÖō®ōĪ 1969 ŔĀŔä ŔĀōĪŔÜō≥ōßōĆ ō≠ŔÉŔÖ ŔÉōĪō© ŔāōĮŔÖ ŔĀōĪŔÜō≥Ŕä.[1][2][3] ō≠ōĶŔĄ ōĻŔĄÔŅĹ...

Henk LubberdingHenk Lubberding en 1977.InformationsNaissance 4 ao√Ľt 1953 (70 ans)VoorstNationalit√© n√©erlandaise√Čquipes professionnelles 1977TI-Raleigh1978-1979TI-Raleigh-Mac Gregor1980-1981TI-Raleigh-Creda1982-1983TI-Raleigh-Campagnolo01.1984-06.1987Panasonic06.1987-12.1989Panasonic-Isostar1990-1992Panasonic-SportlifePrincipales victoires 2 championnats Champion des Pays-Bas sur route 1978 et 19791 classement annexe de grand tour Classement du meilleur jeune du Tour de France 19783 ÔŅĹ...

Self-help and meditation program The Silva Method is a self-help and meditation program developed by José Silva. It claims to increase an individual's abilities through relaxation, development of higher brain functions, and psychic abilities such as clairvoyance.[1] It has been variously classified as a self-religion,[2] a new religious movement, and a cult,[3] and has been criticised as pseudoscience.[4] Biography José Silva, an electronics repairman, grew u...

–£ —ć—ā–ĺ–≥–ĺ —ā–Ķ—Ä–ľ–ł–Ĺ–į —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –ł –ī—Ä—É–≥–ł–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź, —Ā–ľ. –ß–į–Ļ–ļ–ł (–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź). –ß–į–Ļ–ļ–ł –Ē–ĺ–ľ–ł–Ĺ–ł–ļ–į–Ĺ—Ā–ļ–į—Ź —á–į–Ļ–ļ–į–ó–į–Ņ–į–ī–Ĺ–į—Ź —á–į–Ļ–ļ–į–ö–į–Ľ–ł—Ą–ĺ—Ä–Ĺ–ł–Ļ—Ā–ļ–į—Ź —á–į–Ļ–ļ–į–ú–ĺ—Ä—Ā–ļ–į—Ź —á–į–Ļ–ļ–į –Ě–į—É—á–Ĺ–į—Ź –ļ–Ľ–į—Ā—Ā–ł—Ą–ł–ļ–į—Ü–ł—Ź –Ē–ĺ–ľ–Ķ–Ĺ:–≠—É–ļ–į—Ä–ł–ĺ—ā—č–¶–į—Ä—Ā—ā–≤–ĺ:–Ė–ł–≤–ĺ—ā–Ĺ—č–Ķ–ü–ĺ–ī—Ü–į—Ä—Ā—ā–≤–ĺ:–≠—É–ľ–Ķ—ā–į–∑–ĺ–ł–Ď–Ķ–∑ —Ä–į–Ĺ–≥–į:–Ē–≤—É—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ-—Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ—č–Ķ–Ď–Ķ–∑ —Ä–į–Ĺ–≥–į:–í—ā–ĺ—Ä–ł—á...

American model Samantha HoopesHoopes in 2014Born (1991-02-10) February 10, 1991 (age 33)Doylestown, Pennsylvania, U.S.Children2Modeling informationHeight5 ft 8 in (1.73 m)Hair colorBlondeBrown (natural)Eye colorHazelAgency MGM Models (Hamburg)[1] Samantha Hoopes (born February 10, 1991) is an American model known for her appearances in the Sports Illustrated Swimsuit Issue from 2014 to 2020.[2] Early life and education Samatha Hoopes was born on February 10...

Moscow Metro station Barrikadnaya–Ď–į—Ä—Ä–ł–ļ–į–ī–Ĺ–į—ŹMoscow Metro stationGeneral informationLocationPresnensky District,Central Administrative OkrugMoscowRussiaCoordinates55¬į45‚Ä≤40‚Ä≥N 37¬į34‚Ä≤46‚Ä≥E / 55.7612¬įN 37.5795¬įE / 55.7612; 37.5795Owned byMoskovsky MetropolitenLine(s) Tagansko-Krasnopresnenskaya linePlatforms1 island platformTracks2ConnectionsBus: 116Trolleybus: 35ConstructionDepth30 metres (98 ft)Platform levels1ParkingNoOther informationStat...

ś≠§śĚ°ÁõģŚļŹŤ®ÄÁꆍäāś≤°śúČŚÖÖŚąÜśÄĽÁĽďŚÖ®śĖáŚÜÖŚģĻŤ¶ĀÁāĻ„Äā (2019ŚĻī3śúą21śó•)ŤĮ∑ŤÄÉŤôϜȩŚÖÖŚļŹŤ®ÄԾƜłÖśôįś¶āŤŅįśĚ°ÁõģśČÄśúČťá杼ě„ÄāŤĮ∑Śú®śĚ°ÁõģÁöĄŤģ®Ťģļť°ĶŤģ®Ťģļś≠§ťóģťĘė„Äā ŚďąŤź®ŚÖčśĖĮŚĚ¶ÁłĹÁĶĪŚďąŤĖ©ŚÖčÁłĹÁĶĪśóóÁŹĺšĽĽ“ö–į—Ā—č–ľ-–Ė–ĺ–ľ–į—Ä—ā –ö–Ķ–ľ–Ķ–Ľ“Ī–Ľ—č –Ę–ĺ“õ–į–Ķ–≤Ść°ÁĎüŚßÜŤč•ť©¨ŚįĒÁČĻ¬∑śČėŚć°ŤÄ∂Ś§ęŤá™2019ŚĻī3śúą20śó•Śú®šĽĽšĽĽśúü7ŚĻīť¶ĖšĽĽŚä™ŚįĒŤčŹšłĻ¬∑Áļ≥śČéŚįĒŚ∑īŤÄ∂Ś§ęŤģĺÁęč1990ŚĻī4śúą24śó•ÔľąŚďąŤĖ©ŚÖčŤėáÁ∂≠ŚüÉÁ§ĺśúÉšłĽÁĺ©ŚÖĪŚíĆŚúčÁłĹÁĶĪÔľČ ŚďąŤź®ŚÖčśĖĮŚĚ¶ ŚďąŤź®ŚÖčśĖĮŚĚ¶śĒŅŚļú...

ōßŔĄōĻŔĄōßŔāōßō™ ōßŔĄōļōßŔÖō®Ŕäō© ōßŔĄŔÉŔąō®Ŕäō© ōļōßŔÖō®Ŕäōß ŔÉŔąō®ōß ōļōßŔÖō®Ŕäōß ŔÉŔąō®ōß ō™ōĻōĮŔäŔĄ ŔÖōĶōĮōĪŔä - ō™ōĻōĮŔäŔĄ ōßŔĄōĻŔĄōßŔāōßō™ ōßŔĄōļōßŔÖō®Ŕäō© ōßŔĄŔÉŔąō®Ŕäō© ŔáŔä ōßŔĄōĻŔĄōßŔāōßō™ ōßŔĄōęŔÜōßō¶Ŕäō© ōßŔĄō™Ŕä ō™ō¨ŔÖōĻ ō®ŔäŔÜ ōļōßŔÖō®Ŕäōß ŔąŔÉŔąō®ōß.[1][2][3][4][5] ŔÖŔāōßōĪŔÜō© ō®ŔäŔÜ ōßŔĄō®ŔĄōĮŔäŔÜ ŔáōįŔá ŔÖŔāōßōĪŔÜō© ōĻōßŔÖō© ŔąŔÖōĪō¨ōĻŔäō© ŔĄŔĄōĮŔąŔĄō™ŔäŔÜ: Ŕąō¨Ŕá ōßŔĄŔÖŔāōßōĪŔÜō© ōļōßŔÖō®Ŕäōß ŔÉŔąō®ōß ÔŅĹ...

Azikin Solthan Anggota Dewan Perwakilan RakyatPetahanaMulai menjabat 1 Oktober 2014Daerah pemilihanSulawesi Selatan IBupati Bantaeng ke-8Masa jabatan1998‚Äď2008PresidenB. J. Habibie Abdurrahman Wahid Megawati Soekarnoputri Susilo Bambang YudhoyonoGubernurZainal Basri Palaguna Amin Syam Syahrul Yasin LimpoWakilAbd. Azis Muttalib (2003‚Äď2008)PendahuluSaid SaggafPenggantiNurdin Abdullah Informasi pribadiLahir7 Agustus 1953 (umur 70)Bantaeng, Sulawesi, IndonesiaKebangsaanIndonesiaPa...

Il tricloruro di cromo o cloruro di cromo(III) √® il composto chimico di formula CrCl3. Esiste in forme diverse a seconda del grado di idratazione. Anidro, √® un solido cristallino viola inodore, insolubile in acqua. Esiste inoltre il tricloruro di cromo esaidrato, che si pu√≤ isolare in tre isomeri differenti. Indice 1 Tricloruro di cromo anidro, CrCl3 1.1 Struttura 1.2 Sintesi 1.3 Reattivit√† 2 Tricloruro di cromo esaidrato, CrCl3‚ÄĘ6H2O 3 Sicurezza 4 Note 5 Bibliografia 6 Altri progetti Tr...

Public park in Queens, New York Baisley Pond ParkView across Baisley PondTypePublic parkLocationQueens, New York City, NY, United StatesCoordinates40¬į40‚Ä≤40‚Ä≥N 73¬į47‚Ä≤5‚Ä≥W / 40.67778¬įN 73.78472¬įW / 40.67778; -73.78472Area109.61 acres (44.36 ha)Created1919Operated byNYC ParksStatusOpen all year Baisley Pond Park is a public park located in the southeastern part of Queens, New York City, bordering the neighborhoods of South Jamaica, Rochdale, and St. A...

Biblical figure identified with fallen angel For other uses, see Azazel (disambiguation). Not to be confused with Azazil or Azrael. And Aaron shall cast lots over the two goats, one lot for the LORD and the other lot for Azazel. Lincoln Cathedral In the Hebrew Bible, the name Azazel (/…ôňąze…™z…ôl, ňą√¶z…ôňĆz…õl/; Hebrew: ◊Ę÷≤◊Ė÷ł◊ź◊Ė÷Ķ◊ú ŅńāzńĀ ĺzńďl; Arabic: ōĻō≤ōßō≤ŔäŔĄ, romanized: ŅAzńĀzńęl) represents a desolate place where a scapegoat bearing the sins of the Jews was sent during ...

Governing body for basketball in the United States USA BasketballFormation1974; 50 years ago (1974)TypeNational Governing Body (NGB)LocationColorado Springs, ColoradoRegion served United StatesOfficial language English, SpanishChairmanMartin DempseyKey peopleJim Tooley (CEO) Chauncey Billups (Athlete representative) Kim Bohuny (NBA representative)AffiliationsFIBAFIBA AmericasWebsitewww.usab.com USA Basketball (USAB) is a non-profit organization and the governing body for bas...

2013 soundtrack album by Ramin DjawadiGame of Thrones: Season 3Soundtrack album by Ramin DjawadiReleasedJune 4, 2013 (2013-06-04)GenreSoundtrackLength53:12LabelWaterTower MusicProducerRamin DjawadiGame of Thrones music chronology Game of Thrones: Season 2(2012) Game of Thrones: Season 3(2013) Game of Thrones: Season 4(2014) Ramin Djawadi soundtrack chronology Red Dawn(2012) Game of Thrones: Season 3(2013) Pacific Rim(2013) Singles from Game of Thrones: Season 3 The Bear...






