ÐÐūÐŋÐūÐŧÐ―ÐĩÐ―ÐļÐĩ ŅзÐŧа
|
Read other articles:
Heritage-listed military building in Adelaide, South Australia Headquarters Building, Keswick BarracksKeswick Barracks, Adelaide, c.1918LocationAnzac Highway, Keswick, South Australia, AustraliaCoordinates34°56âē38âģS 138°34âē57âģE / 34.9438°S 138.5824°E / -34.9438; 138.5824 Commonwealth Heritage ListOfficial nameHeadquarters Building 32, Keswick BarracksTypeListed place (Historic)Designated22 June 2004Reference no.105308 Location of Headquarters Building,...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala. Honda Civic GLi hatchback 3 pintu (di Indonesia dikenal dengan nama Civic Estilo) Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipert...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sachaai â news · newspapers · books · scholar · JSTOR (May 2018) (Learn how and when to remove this template message) Indian filmSachaaiPosterDirected byK. ShankarScreenplay byK. ShankarProduced byM.C. RamamurthyStarringShammi KapoorSanjeev KumarSadhanaCinematographySudhin Maju...

Cet article est une ÃĐbauche concernant une ÃĐlection en France. Vous pouvez partager vos connaissances en lâamÃĐliorant (comment ?) selon les recommandations des projets correspondants. 1965 1971 Ãlections sÃĐnatoriales françaises de 1968 22 septembre 1968 RI â François Schleiter SÃĐnateurs ÃĐlus 54 6 SOC â Antoine CourriÃĻre SÃĐnateurs ÃĐlus 52 UCDP â AndrÃĐ Colin SÃĐnateurs ÃĐlus 47 9 GD â Lucien Grand SÃĐnateurs ÃĐlus ...

American Catholic prelate (born1949) His EminenceJames Michael HarveyArchpriest of the Basilica of Saint Paul Outside the WallsCardinal-Deacon of San Pio V a Villa CarpegnaHarvey in 2013ChurchCatholic ChurchLatin ChurchSeeBasilica of Saint Paul Outside the WallsAppointedNovember 23, 2012PredecessorFrancesco MonterisiOrdersOrdinationJune 29, 1975by Pope Paul VIConsecrationMarch 19, 1998by Pope John Paul IICreated cardinalNovember 24, 2012by Pope Benedict XVIRankCardinal-DeaconPersona...

1939â1940 massacres in Pomerania committed by Nazi Germany Intelligenzaktion PommernPart of Generalplan OstMass shootings in Darzlubska WildernessPomerania: places of executions marked in redLocationGerman occupied Pomeranian Voivodeship, Free City of Danzig annexed as Reichsgau Danzig-West Prussia in Polish areas annexed by Nazi GermanyDate1939â1940TargetPolish intellectuals and the upper classes from prescribed list.Attack typeMassacresWeaponsAutomatic weaponsDeaths23,000 [1]Per...

Chemical compound JWH-398Legal statusLegal status CA: Schedule II DE: NpSG (Industrial and scientific use only) UK: Class B US: Schedule I Illegal in Latvia[1] Identifiers IUPAC name 1-Pentyl-3-(4-chloro-1-naphthoyl)indole CAS Number1292765-18-4 NChemSpider28647395 NUNIIRX0E95S90HCompTox Dashboard (EPA)DTXSID40156131 Chemical and physical dataFormulaC24H22ClNOMolar mass375.90 g·molâ13D model (JSmol)Interactive image SMILES c14ccccc1n(CCCCC)cc4C(=O...
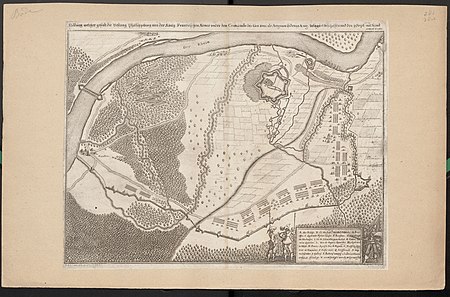
Siege of PhilippsburgPart of the Thirty Years' WarPainting of the siege by Jean-Baptiste Le Paon (1769)Date25 August â 12 September 1644(2 weeks and 4 days)LocationPhilippsburg, Prince-Bishopric of Speyer, Holy Roman Empire,(present-day Germany)49°14âē13âģN 8°27âē17âģE / 49.2370°N 8.4548°E / 49.2370; 8.4548Result French victoryBelligerents France Holy Roman EmpireCommanders and leaders Duc d'Enghien Vicomte de Turenne Duc de Gramont Casp...

Ganga (Cyrillic: ÐÐ°Ð―Ðģа) is a type of singing that originated from rural Dinaric mountain region. It is most commonly found in the regions of Herzegovina and Dalmatia, but it can also be found to an extent in western Bosnia, Lika, Kordun and rural areas of north-west Montenegro. It is characterized by a lone singer singing a single line of lyrics, followed by others joining in, using a vocal style that is best described as a wail. Ganga has historically been closely associated with the re...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Daftar stasiun televisi di Sumatera Selatan â berita · surat kabar · buku · cendekiawan · JSTOR (September 2021) Berikut ini adalah daftar stasiun televisi di Sumatera Selatan. Catatan: Kecuali pada stasiun t...

NBC affiliate in Cleveland For the television station in Philadelphia that currently uses the callsign formerly used by WKYC, see KYW-TV. WKYCClevelandâAkron, OhioUnited StatesCityCleveland, OhioChannelsDigital: 19 (UHF)Virtual: 3BrandingWKYC Studios, 3 NewsProgrammingAffiliations3.1: NBCfor others, see § SubchannelsOwnershipOwnerTegna Inc.(WKYC-TV, LLC)HistoryFirst air dateOctober 31, 1948(75 years ago) (1948-10-31)Former call signsWNBK (1948â1956)KYW-TV (1956â1965)WKYC...

PausUrbanus IVAwal masa kepausan29 Agustus 1261Akhir masa kepausan2 Oktober 1264PendahuluAleksander IVPenerusKlemens IVInformasi pribadiNama lahirJacques PantalÃĐonLahirc. 1195Troyes, Champagne, PrancisWafat2 Oktober 1264Perugia, Negara Gereja, Kekaisaran Romawi SuciPaus lainnya yang bernama Urbanus Paus Urbanus IV (lahir 1195 di Troyes, Prancis meninggal di Perugia 2 Oktober 1264), lahir Jacques PantalÃĐon, adalah Paus, dari tahun 1261 hingga tahun 1264. Referensi David Abulafia, 1988. Frede...

FÃķrsta sidan av regeringsformen i Finlands fÃķrfattningssamling nr. 94/1919. Regeringsformen (FFS 94/1919), som trÃĪdde i kraft den 17 juli 1919, var det sjÃĪlvstÃĪndiga Finlands fÃķrsta egna grundlag. Den ersatte den gamla gustavianska regeringsformen frÃĨn 1772, med sitt tillÃĪgg frÃĨn 1789, FÃķrenings- och sÃĪkerhetsakten. Den ersattes i sin tur ÃĨr 2000 av Finlands grundlag. Bakgrund Huvudartikel: FÃķrfattningsstriden i Finland Tiden frÃĨn ryska revolutionen och Finlands sjÃĪlvstÃĪnd...

CannelleL'ourse Cannelle (1989-2004) naturalisÃĐe et exposÃĐe au MusÃĐum de Toulouse.InformationsEspÃĻce Ours brun, ours brunSexe FemelleDate de naissance 1989Lieu de naissance PyrÃĐnÃĐes-AtlantiquesLieu de vie PyrÃĐnÃĐesDate de dÃĐcÃĻs 1er novembre 2004Lieu de dÃĐcÃĻs UrdosCause de dÃĐcÃĻs Chasse, blessure par arme à feuMasse 95 kgPÃĻre InconnuMÃĻre InconnueEnfant Cannellitomodifier - modifier le code - modifier Wikidata Cannelle ÃĐtait la derniÃĻre reprÃĐsentante d'une population d'ours de...

2016åđīįūåįļ―įĩąéļč ← 2012 2016åđī11æ8æĨ 2020 → 538åéļčäššååļä―įēåé270įĨĻæ°æčŠŋæĨæįĨĻį55.7%[1][2] âē 0.8 % č·æåäšš åįī·å·æŪ åļæč·å æé æŋå å ąåéŧĻ æ°äļŧå åŪķéå· įīįīå· įīįīå· įŦéææĄĢ čŋå ·å―æŊ čå§Â·åąæĐ éäļūäššįĨĻ 304[3][4][čĻŧ 1] 227[5] čåšå·/į 30 + į·Ž-2 20 + DC æ°éļåūįĨĻ 62,984,828[6] 65,853,514[6]...

Westhoek françaisFlandre flamingante Pays France RÃĐgion française Hauts-de-France Le Westhoek est la partie nord de la Flandre française. modifier Le Westhoek français, appelÃĐ ÃĐgalement Flandre flamingante[1], est un territoire situÃĐ en France qui correspond à la partie ouest du Westhoek et à la partie nord de la Flandre française. Sur le plan administratif, il correspond à peu prÃĻs à l'arrondissement de Dunkerque dans le dÃĐpartement du Nord. Sur le plan linguistique, il...

Persatuan Nasional Vlaam Vlaams Nationaal VerbondKetua umumStaf de Clerq (1933 â 1942)Hendrik Elias (1942 â 1944)Pendiri Daftar Hendrik Elias Reimond Tollenaere GÃĐrard RomsÃĐe Ernest Van den Berghe Frans Daels Edgard Delvo Jeroom Leuridan Raymond Speleers Dibentuk8 Oktober 1933Dibubarkan2 September 1944Didahului olehFrontpartijKantor pusatBrussel, BelgiaSurat kabarVolk en StaatSayap ParamiliterFlemish Legion (1941 â 1945) (Dutch: Vlaams Legioen)IdeologiFasismeNasionalismeBelanda R...

Thai football club Football clubPrime Bangkok āļāļĢāļēāļĄ āđāļāļāļāđāļāļFull namePrime Bangkok Football ClubNickname(s)The Thunder EaglesFounded2006; 18 years ago (2006), as Bangkok North Central ASSN2016; 8 years ago (2016), as Air Force Robinson2020; 4 years ago (2020), as Prime BangkokGroundRamkhamhaeng University StadiumBang Kapi, Bangkok, ThailandCapacity6,000ChairmanJatuporn PramualbanHead CoachThidarat WivasukLeagueThai Leag...

Caso de los narcosobrinos Campo (segundo de la izquierda) y Flores (tercero desde la derecha) tras su arrestoLocalizaciÃģnPaÃs Haità HaitÃLugar Puerto PrÃncipeDatos generalesEstado Venezuela VenezuelaTipo NarcotrÃĄficoHistÃģricoFecha 10 de noviembre de 2015[editar datos en Wikidata] El incidente de los narcosobrinos es un caso que involucra a dos sobrinos de Cilia Flores, esposa del presidente venezolano NicolÃĄs Maduro. Los detenidos, EfraÃn Antonio Campo Flores y Francis...

Questa voce sull'argomento calciatori argentini ÃĻ solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Gabriel BÃĄezNazionalità Argentina Calcio RuoloCentrocampista Squadra Nacional CarrieraGiovanili Newell's Old Boys Squadre di club1 2015-2017 Newell's Old Boys16 (0)2017-2019â Venados55 (3)2019-2020 Newell's Old Boys0 (0)2020-2021 Cerro Largo12 (1)2021-2022 Sol de...






















