Группа классов преобразований поверхности
|
Read other articles:

Ww WwUrsprungProtokanaiskt (wav)Feniciskt (wāw)Besläktade bokstäver i andra alfabetArabisktو (wāw)Hebreisktו (vav)Arameiskt (waw)GrekisktΥυ (Ypsilon)KyrillisktУуTeknisktMorse ISO/IEC 8859-1W:87 / w:119UnicodeW:U+0057 / w:U+0077BokstaveringWilhelm/Whiskey W [dubbel-ve] är den tjugotredje bokstaven i det moderna latinska alfabetet. Bokstaven räknades i den svenska versionen av detta alfabet fram till 2006 som en variant av V...

Strada statale 520del CerasoDenominazioni successiveStrada regionale 520 del Ceraso LocalizzazioneStato Italia Regioni Abruzzo DatiClassificazioneStrada statale InizioOvindoli FineVado Ceraso Lunghezza4,200[1] km Provvedimento di istituzioneD.M. 19/03/1969 - G.U. 164 del 2/07/1969[2] GestoreTratte ANAS: nessuna (dal 2001 la gestione è passata alla Provincia dell'Aquila) Manuale La ex strada statale 520 del Ceraso (SS 520), ora strada regionale 520 del Ceraso (SR 520...

العلاقات البحرينية الغرينادية البحرين غرينادا البحرين غرينادا تعديل مصدري - تعديل العلاقات البحرينية الغرينادية هي العلاقات الثنائية التي تجمع بين البحرين وغرينادا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه ...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Bensin – berita · surat kabar · buku · cendekiawan · JSTOR (Februari 2014) Untuk senyawa kimia dengan nama yang mirip, lihat Benzena. Sebuah toples berisi bensin Bensin (dari Belanda: benzinecode: nl is depre...

2004 French film by Enki Bilal ImmortalTheatrical release posterDirected byEnki BilalWritten byEnki Bilal (scenario, adaptation and dialogue)Serge Lehman (script)Based onComic book La Foire aux immortels by Enki BilalProduced byCharles GassotStarring Linda Hardy Thomas Kretschmann Charlotte Rampling Frédéric Pierrot Jean-Louis Trintignant CinematographyPascal GennesseauxEdited byVéronique ParnetMusic byGoran VejvodaProductioncompaniesDuran Entertainment Quantic DreamDistributed byUGC Fox D...

Newspaper serving Bangor, Maine, United States Bangor Daily NewsThe May 22, 2009 front page of The Bangor Daily NewsTypeDaily newspaperFormatBroadsheetOwner(s)Bangor Publishing CompanyFounder(s)J. Norman TowleEdward H. BlakePublisherRichard J. WarrenPresidentTodd BenoitEditorDan MacLeodFoundedJune 18, 1889; 134 years ago (1889-06-18)Headquarters1 Merchants Plaza,Bangor, Maine, U.S.CountryUnited StatesISSN0892-8738 (print) 2643-7457 (web)OCLC number8818350 Websiteww...

American record label Riverside RecordsFounded1953 (1953)FounderBill Grauer, Jr Orrin KeepnewsDefunct1964 (1964)StatusDefunctGenreJazz, blues, folkCountry of originU.S.LocationNew York City Riverside Records was an American jazz record company and label. Founded by Orrin Keepnews and Bill Grauer, Jr, under his firm Bill Grauer Productions in 1953, the label played an important role in the jazz record industry for a decade.[1][2] Riverside headquarters were located in...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Nutria asiática de garras pequeñas Estado de conservaciónVulnerable (UICN 3.1)[1]TaxonomíaReino: AnimaliaFilo: ChordataSubfilo: VertebrataClase: MammaliaSubclase: TheriaInfraclase: PlacentaliaOrden: CarnivoraSuborden: CaniformiaFamilia: MustelidaeSubfamilia: LutrinaeGénero: AonyxEspecie: A. cinerea(Illiger, 1815)Distribución Distribución de la nutria enanaSinonimia Lutra cinerea Illiger, 1815 Aonyx cinereus (Illiger, 1815) por error ortográfico Amblonyx cinereus (Il...

Russian professional footballer In this name that follows Eastern Slavic naming customs, the patronymic is Yevgenyevich and the family name is Belyayev. Roman Belyayev Roman Belyayev in 2011Personal informationFull name Roman Yevgenyevich BelyayevDate of birth (1988-02-14) 14 February 1988 (age 36)Place of birth Novosibirsk, Russian SFSRHeight 1.80 m (5 ft 11 in)Position(s) Midfielder/ForwardYouth career FC Sibir NovosibirskSenior career*Years Team Apps (Gls)2007–200...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Beltway Boys – news · newspapers · books · scholar · JSTOR (May 2020) (Learn how and when to remove this message) American TV series or program The Beltway BoysPresented byMort KondrackeFred BarnesCountry of originUnited StatesNo. of episodesUnknownProducti...

Electrical interconnector between the UK and France ElecLinkMap of ElecLinkLocationCountryUnited Kingdom, FranceCoordinates51°5′54.2″N 1°8′40.9″E / 51.098389°N 1.144694°E / 51.098389; 1.144694 (Folkestone Converter Station)50°55′12.7″N 1°46′50.2″E / 50.920194°N 1.780611°E / 50.920194; 1.780611 (Peuplingues Converter Station)General directionNorth–SouthFromFolkestone, United KingdomPasses throughEnglish C...

Language of the Yuchi people in the southeastern United States YuchiEucheeTsoyahaNative toUnited StatesRegionEast central OklahomaEthnicity1,500 Yuchi (2007)[1]Native speakers0[2] (2021)12 L2 speakers (2016)[1]Language familyLanguage isolateLanguage codesISO 639-3yucGlottologyuch1247ELPYuchiDistribution of Yuchi at the time of European contactThis article contains IPA phonetic symbols. Without proper rendering support, you may see question marks, boxes, or ot...

Firefighting equipment This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (January 2017) (Learn how and when to remove this message) A deck gun in the foreground puts water through a window while a ladder-mounted master stream in the background directs water through the collapsed roof. Fixed fire monitor at a plastic manufacturi...

Australian rules football club Not to be confused with Coburg Amateurs Football Club or FC Coburg. Australian rules football club Coburg Football ClubNamesFull nameCoburg Football Club Limited[1]Former name(s)Coburg-Fitzroy Football Club (1999–2000)Nickname(s)Lions, Burgers[2]Former nickname(s)Tigers (2001–2013)Club songTune of California, Here I Come2023 seasonHome-and-away season21stClub detailsFounded1891; 133 years ago (1891)Colours Navy ...

Argentine-Chilean footballer (born 1988) In this Spanish name, the first or paternal surname is Buonanotte and the second or maternal family name is Rende. Diego Buonanotte Buonanotte with Universidad Católica in 2019Personal informationFull name Diego Mario Buonanotte RendeDate of birth (1988-04-19) 19 April 1988 (age 36)Place of birth Teodelina, ArgentinaHeight 1.60 m (5 ft 3 in)[1]Position(s) Attacking midfielder / WingerTeam informationCurrent team O'H...

Voce principale: Associazione Calcio Savoia 1908. Società Sportiva SavoiaStagione 2002-2003 Sport calcio Squadra Savoia Allenatore Alberto Urban (1ª-14ª) poi Piero Cucchi (15ª-19ª) poi Guglielmo Ricciardi (20ª-34ª) Presidente Dario Pasquariello Serie D6º posto Coppa Italia Serie DPrimo turno Maggiori presenzeCampionato: Bucciarelli, Cerrato, Oriente (29)Totale: Bucciarelli, Cerrato, Oriente (29) Miglior marcatoreCampionato: Sgambati (10)Totale: Sgambati (10) StadioAlfredo Giraud...
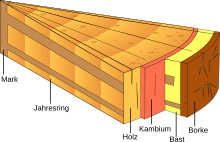
Der Titel dieses Artikels ist mehrdeutig. Weitere Bedeutungen sind unter Borke (Begriffsklärung) aufgeführt. Borke einer 80-jährigen Weißtanne Querschnitt durch einen fünfjährigen Kiefernstamm Die Borke ist die äußerste Schicht der Rinde bei den meisten Bäumen. Sie entsteht aus dem Kork und abgestorbenen Teilen des Bastes. Die Borke schützt die darunterliegenden Schichten des Baumstamms vor physikalischen Einflüssen wie Hitze, Frost, Regen, Wind, Sonne, Feuer und mechanischen Einw...

City in Apulia, Italy This article is about the city in Italy. For other uses, see Bari (disambiguation). Comune in Apulia, ItalyBari Bare (Neapolitan)ComuneComune di BariLungomare di BariTeatro PetruzzelliPiazza del ferrareseBasilica di San NicolaPiazza Mercantile FlagCoat of armsLocation of Bari BariLocation of Bari in ItalyShow map of ItalyBariBari (Apulia)Show map of ApuliaCoordinates: 41°07′31″N 16°52′0″E / 41.12528°N 16.86667°E / 41.12528; 16.866...



















