Выворачивание сферы
|
Read other articles:

Chemical compound Not to be confused with cinazepam, clonazepam, or camazepam. CinolazepamClinical dataTrade namesGerodormAHFS/Drugs.comcinolazepamRoutes ofadministrationOralATC codeN05CD13 (WHO) Legal statusLegal status US: Unscheduled Pharmacokinetic dataBioavailability90–100%MetabolismHepaticElimination half-life3.8 hours[1]ExcretionRenalIdentifiers IUPAC name (RS)-3-[9-Chloro-6-(2-fluorophenyl)-4-hydroxy-3-oxo-2,5-diazabicyclo[5.4.0]undeca-5,8,10,12-tetraen-2-yl]p...

Cette page concerne l'année 1698 du calendrier grégorien. Chronologies 11 septembre : Impôt sur la barbe en Russie. Gravure sur bois contemporaine.Données clés 1695 1696 1697 1698 1699 1700 1701Décennies :1660 1670 1680 1690 1700 1710 1720Siècles :XVe XVIe XVIIe XVIIIe XIXeMillénaires :-Ier Ier IIe IIIe Chronologies thématiques Art Architecture, Arts plastiques (Dessin, Gravure, Peinture et Sculpture), Littérature,...

Nikolay BaskovНиколай БасковLahirNikolay Victorovich Baskov15 Oktober 1976 (umur 47)Balashikha, Uni SovietPekerjaanPenyanyiTahun aktif2000–sekarangSitus webbaskov.ru Nikolay Victorovich Baskov (Rusia: Николай Викторович Басковcode: ru is deprecated , lahir 15 Oktober 1976) adalah seorang penyanyi tenor Rusia yang tampil dalam gaya musik opera dan populer.[1] Penghargaannya termasuk penghargaan sebagai Seniman Berjasa[2] dan Seni...

Primary road on Saba, Dutch Caribbean The RoadThe Road That Couldn't Be Built.Length14 kilometres (8.7 mi)LocationSaba, NetherlandsFromWell's Bay/ Fort BayMajorjunctionsbranch to Fort BayThe Bottomto St. JohnsWindwardsideHiking Trail to Mount SceneryZion's Hillto sulfur mineJuancho E. Yrausquin AirportToCove BayConstructionConstruction start1938Inauguration1943 The Road is the unofficial name for the cement road that connects the villages of Saba, Netherlands, a Caribbean island. It is n...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 2024 BW Open – news · newspapers · books · scholar · JSTOR (March 2024) Tennis tournament2024 BW OpenDate23–28 JanuaryEdition2ndSurfaceHard (indoor)LocationOttignies-Louvain-la-Neuve, BelgiumChampionsSingles Leandro RiediDoubles Luke Johnson / Skand...

Ne doit pas être confondu avec Denise Mützenberg. Willi MünzenbergWilli Münzenberg.FonctionDéputé au Reichstag sous la république de Weimarjusqu'en 1933BiographieNaissance 14 août 1889ErfurtDécès 22 juin 1940 ou 17 octobre 1940Saint-MarcellinNationalité allemandeDomicile BerlinActivités Producteur de cinéma, éditeur, homme politique, journaliste d'opinionAutres informationsPartis politiques Parti communiste d'AllemagneJeunesse socialiste suisseSignaturemodifier - modifier le co...

Peter Arthur Diamond Premio Nobel per l'economia 2010 Peter Arthur Diamond (New York, 29 aprile 1940) è un economista statunitense. È noto per le proprie analisi sulle politiche di sicurezza sociale negli USA e per il suo lavoro presso l'Advisory Council on Social Security tra il 1980 e il 1990. Nel 2010 riceve il Premio Nobel per l'economia insieme con Dale Mortensen e Christopher Pissarides «per le loro analisi sui mercati che presentano frizioni di ricerca». Biografia Dopo un bachelor ...

Samsurizal Tombolotutu Bupati Parigi Moutong ke-2PetahanaMulai menjabat 17 Juni 2011 (Pelaksana tugas sampai 14 Juli 2011)PresidenSusilo Bambang YudhoyonoJoko WidodoGubernurLongki DjanggolaRusdy MasturaWakilBadrun NggaiPendahuluLongki DjanggolaPenggantiPetahanaWakil Bupati Parigi Moutong ke-2Masa jabatan9 Oktober 2008 – 17 Juni 2011PresidenSusilo Bambang YudhoyonoGubernurBandjela PaliudjuLongki DjanggolaPendahuluAsmir NtosaPenggantiKemal Toana Informasi pribadiLahir3 Ma...

Masjid Namirah. Masjid Namirah adalah masjid yang terletak di perbatasan antara Al-Haram dan Arafah, tepatnya di arah barat Jabal Rahmah (Bukit Arafah). Masjid dua lantai yang memiliki luas 124.000 m2 ini mampu menampung jamaah hingga 300.000 orang.[1] Pasca perluasan, sebagian masjid ini berada di luar kawasan arafah, sehingga diberikan tanda informasi dan pengumuman tentang perbatasannya agar jamaah haji tetap berada di lingkungan Arafah.[2] Pada musim haji setiap tahunnya m...
Sclafani Bagni— Comune —Comune di Sclafani Bagni Vị trí của Sclafani Bagni Lỗi Lua trong Mô_đun:Location_map tại dòng 583: Không tìm thấy trang định rõ bản đồ định vị. "Mô đun:Location map/data/Italy Sicilia", "Bản mẫu:Bản đồ định vị Italy Sicilia", và "Bản mẫu:Location map Italy Sicilia" đều không tồn tại.Vị trí của Sclafani Bagni tại ÝQuốc giaÝVùngSiciliaT�...

Species of primate in Malaysia and Singapore Raffles' banded langur[1] Presbytis femoralis in Singapore Conservation status Critically Endangered (IUCN 3.1)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Primates Suborder: Haplorhini Infraorder: Simiiformes Family: Cercopithecidae Genus: Presbytis Species: P. femoralis Binomial name Presbytis femoralis(Martin, 1838) Raffles' banded langur range in Singapore a...

Докладніше: Втрати силових структур внаслідок російського вторгнення в Україну У статті наведено список втрат українських військовослужбовців у російсько-українській війні, починаючи з 17 липня 2022 року по 31 липня 2022 року (включно). Втрати з українського боку публікуют...
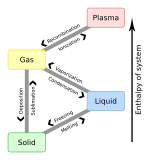
Heating a liquid to a temperature above its boiling point without boiling This article is about the phenomenon where a liquid can exist in a metastable state above its boiling point. For pressurized water above 100 °C, see superheated water. For the device used in steam engines, see superheater. For the 'superheat' used in vapor-compression refrigeration, see Vapor-compression refrigeration § Thermodynamic analysis of the system. In thermodynamics, superheating (sometimes referred to a...

Seorang wanita sedang menikmati segelas kopi susu di sebuah kafe. Ngopi cantik adalah istilah untuk menyebut tren gaya hidup dalam menikmati kopi khususnya pada kalangan perempuan perkotaan di Indonesia. Ngopi cantik dipahami sebagai kegiatan berkumpul dan mengobrol sesama perempuan di kedai kopi atau kafe yang nyaman, biasanya dalam keadaan telah berdandan cantik.[1][2][3][4] Kegiatan ini biasanya diikuti dengan berfoto bersama untuk kemudian diunggah ke media...

Poly(ethyl methacrylate) Names Other names Ethyl 2-methyl-2-propenoate homopolymer[1]Ethylmethacrylate,homopolymer2-Propenoic acid, ethyl ester, homopolymer[2] Identifiers CAS Number 9003-42-3[3] Abbreviations PEMA ChEBI CHEBI:53221[4] ChemSpider none ECHA InfoCard 100.131.117 CompTox Dashboard (EPA) DTXSID701009717 Properties Chemical formula (C6H10O2)n Appearance powder [5] Solubility in water insoluble in water [6] Except where otherwi...

FeelLagu oleh Kumi Kodadari album Best: Second SessionDirilis11 Januari 2006 (JP)FormatCDDirekam2005GenreJ-pop, soulLabelRhythm ZoneRZCD-45306 (Jepang, CD)SM EntertainmentSMJTCD-094 (Korea, CD)PenciptaKoda Kumi, Hitoshi Shimono Feel (ditulis sebagai feel) adalah sebuah lagu R&B karya penyanyi dan penulis Jepang Kumi Koda. Untuk lagu tersebut, ia giat berkarya dengan komponis Hitoshi Shimono, yang mengkomposisikan instrumentalnya. Pranala luar Avex Network (2005), Kumi Koda Official Web Si...

British war material being offloaded in Takoradi in the Gold Coast The involvement of the Gold Coast (modern-day Ghana) in World War II began with the declaration of war on Nazi Germany by the British Empire in September, 1939. Though no combat occurred in the Gold Coast colony, the colony supplied resources and manpower for the Allies. Home Front Two days after the German invasion of Poland on 1 September 1939, the United Kingdom declared war on Nazi Germany. Due to the German loss in World...

LGBT rights in ItalyItaly wrapped in the colors of the rainbow flagStatusSame-sex activity legal nationwide since 1890, with an equal age of consent;[1] legal in Tuscany since 1853 (as the Grand Duchy of Tuscany),[2][3] in Sicily since 1819 (as the Kingdom of the Two Sicilies)[4][5] and in Naples since 1810 (as the Kingdom of Naples)[4][5][6]Gender identityTransgender people allowed to change legal gender since 1982MilitaryGays,...

彭定康勳爵閣下The Rt Hon. The Lord Patten of Barnes2019年的彭定康 欧洲联盟執委會外交專員任期1999年9月16日—2004年11月22日主席羅馬諾·普羅迪若澤·曼努埃爾·巴羅佐前任莱昂布里坦(英语:Leon Brittan)继任贝尼塔·费雷罗 - 瓦尔德纳(英语:Benita Ferrero-Waldner) 英屬香港第28任總督任期1992年7月9日—1997年6月30日君主伊利沙伯二世布政司霍德爵士陳方安生前任衛奕信勳爵继�...

South African Voortrekker leader (1780-1838) This article is about the person. For the town, see Piet Retief, Mpumalanga. Piet RetiefStatue at the Voortrekker MonumentBornPieter Mauritz Retief(1780-11-12)12 November 1780Soetendal, WagenmakersvalleiDied6 February 1838(1838-02-06) (aged 57)KwaMatiwane, near Hlomo amabuto, uMgungundlovuCause of deathClubbed to death by ZulusBody discoveredc. December 21, 1838 KwaMatiwane, uMgungundlovuResting placeDecember 21, 1838 KwaMatiwane, uMgungu...


![{\displaystyle f_{t}\colon \mathbb {S} ^{2}\to \mathbb {R} ^{3},\ \ t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae4211d5d106c966f3e7f4975dd8e828f560dfd8)















