–í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł
| –°—ā–į—ā—Ć—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā—Ć—é —Ā–Ķ—Ä–ł–ł ¬ę–Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į¬Ľ. |
| –Ě–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł |
|---|
![]() |
|
| –†–į–∑–ī–Ķ–Ľ—č —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł |
|---|
|
| –°–ľ. —ā–į–ļ–∂–Ķ ¬ę–§–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ –Ņ–ĺ—Ä—ā–į–Ľ¬Ľ |
–í—ā–ĺ—Ä–ĺŐĀ–Ķ –Ĺ–į—á–įŐĀ–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–įŐĀ–ľ–ł–ļ–ł (–≤—ā–ĺ—Ä–ĺ–Ļ –∑–į–ļ–ĺ–Ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł) –≤ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–ľ –ł–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä—É–Ķ—ā—Ā—Ź –ļ–į–ļ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ—Ď–Ĺ–Ĺ—č–Ļ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č ‚ĒÄ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł –≤–≤–ĺ–ī–ł—ā –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č[1]. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –∑–į–ļ–ĺ–Ĺ –ĺ–Ī —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł –Ķ—Ď —Ā–≤–ĺ–Ļ—Ā—ā–≤–į—Ö [2].
–í –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ľ–ł–Ī–ĺ –ĺ—Ā—ā–į—Ď—ā—Ā—Ź –Ĺ–Ķ–ł–∑–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, –Ľ–ł–Ī–ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā –≤ –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į—Ö, –ī–ĺ—Ā—ā–ł–≥–į—Ź –ľ–į–ļ—Ā–ł–ľ—É–ľ–į –Ņ—Ä–ł —É—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ł–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł—Ź (–∑–į–ļ–ĺ–Ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł)[3][4]
–Ę–Ķ—Ä–ľ–ł–Ĺ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ī—č–Ľ –ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ –†. –ö–Ľ–į—É–∑–ł—É—Ā–ĺ–ľ –ł–∑ —Ā–Ľ–ĺ–≤–į ŌĄŌĀőŅŌÄő∑ ‚ÄĒ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ, –ł –Ņ—Ä–ł—Ā—ā–į–≤–ļ–ł ŠľźőĹ ‚ÄĒ –≤, –≤–Ĺ—É—ā—Ä—Ć, –≤ —Ü–Ķ–Ľ–ĺ–ľ, –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł–Ķ –≤–Ĺ—É—ā—Ä—Ć [5]. –ü–ĺ–Ĺ—Ź—ā–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, —ā–ĺ—á–Ĺ–Ķ–Ķ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ł–Ľ–ł —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–Ĺ–į–≥–Ľ—Ź–ī–Ĺ—č–ľ, –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č–ľ –ł —ā—Ä—É–ī–Ĺ—č–ľ –ī–Ľ—Ź –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –≤–ĺ—Ā–Ņ—Ä–ł—Ź—ā–ł—Ź, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ĺ–į–Ņ—Ä—Ź–ľ—É—é –Ĺ–Ķ –≤—č—ā–Ķ–ļ–į–Ķ—ā –ł–∑ –Ķ—Ď –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź[6]. –ü–ĺ–Ĺ—Ź—ā—Ć –ł –Ņ—Ä–ĺ—á—É–≤—Ā—ā–≤–ĺ–≤–į—ā—Ć –≥–Ľ—É–Ī–ĺ–ļ–ł–Ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ľ–Ķ–≥—á–Ķ –Ņ–ĺ –Ņ–Ķ—Ä–≤–ĺ–Ĺ–į—á–į–Ľ—Ć–Ĺ—č–ľ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į–ľ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —á–į—Ā—ā–Ĺ—č–ľ–ł —Ā–Ľ—É—á–į—Ź–ľ–ł –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–Ī—Č–Ķ–Ļ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–ł.
–í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć —Ä–į—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—É—é —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ—É—é —ą–ļ–į–Ľ—É, –Ĺ–Ķ –∑–į–≤–ł—Ā—Ź—Č—É—é –ĺ—ā –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–į –≤ –≤—č–Ī–ĺ—Ä–Ķ —ā–Ķ—Ä–ľ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ł —É—Ā—ā—Ä–ĺ–Ļ—Ā—ā–≤–į –ī–Ľ—Ź –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č (—ā–Ķ—Ä–ľ–ĺ–ľ–Ķ—ā—Ä–į)[7].
–í–ľ–Ķ—Ā—ā–Ķ –Ņ–Ķ—Ä–≤–ĺ–Ķ –ł –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–į —Ā–ĺ—Ā—ā–į–≤–Ľ—Ź—é—ā –ĺ—Ā–Ĺ–ĺ–≤—É —Ą–Ķ–Ĺ–ĺ–ľ–Ķ–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –ļ–ĺ—ā–ĺ—Ä—É—é –ľ–ĺ–∂–Ĺ–ĺ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ —Ä–į–∑–≤–ł—ā—É—é —Ā–ł—Ā—ā–Ķ–ľ—É —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ļ —ć—ā–ł—Ö –ī–≤—É—Ö –Ĺ–į—á–į–Ľ. –ü—Ä–ł —ć—ā–ĺ–ľ –ł–∑ –≤—Ā–Ķ—Ö –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ–ľ—č—Ö –Ņ–Ķ—Ä–≤—č–ľ –Ĺ–į—á–į–Ľ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –≤—č–ī–Ķ–Ľ–ł—ā—Ć —Ą–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā—č, –Ĺ–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–į—Č–ł–Ķ –∑–į–ļ–ĺ–Ĺ–į–ľ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ć –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ—ā–Ķ–ļ–į–Ĺ–ł—Ź —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, –Ĺ–į–Ļ—ā–ł –Ņ—Ä–Ķ–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ (–Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–Ķ–Ķ –ł–Ľ–ł –Ĺ–į–ł–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ķ) –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —ć–Ĺ–Ķ—Ä–≥–ł–ł, –ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ–Ķ–∑–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ĺ (–Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ –ł–Ľ–ł –∑–į—ā—Ä–į—á–Ķ–Ĺ–ĺ) –≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–Ķ, –į —ā–į–ļ–∂–Ķ —Ā—Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–į—ā—Ć –ļ—Ä–ł—ā–Ķ—Ä–ł–ł —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł—Ź –≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö. [7][3][4][1].
–ü–Ķ—Ä–≤—č–Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ĺ—ā–Ĺ–ĺ—Ā—Ź—ā—Ā—Ź –ļ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–Ķ XIX –≤–Ķ–ļ–į, –ļ–ĺ–≥–ī–į —Ā—Ą–Ķ—Ä–į –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ĺ–≥—Ä–į–Ĺ–ł—á–ł–≤–į–Ľ–į—Ā—Ć –Ņ—Ä–ĺ—Ā—ā–Ķ–Ļ—ą–ł–ľ–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į–ľ–ł –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —ć–Ĺ–Ķ—Ä–≥–ł–ł, –≤ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į–ľ–ł –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —ā–Ķ–Ņ–Ľ–į –≤ —Ä–į–Ī–ĺ—ā—É. –í –ī–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–ľ —Ā—Ą–Ķ—Ä–į –≤–Ľ–ł—Ź–Ĺ–ł—Ź –Ĺ–į—á–į–Ľ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł —Ä–į—Ā—ą–ł—Ä—Ź–Ľ–į—Ā—Ć –ł —Ā—ā–į–Ľ–į –ĺ—Ö–≤–į—ā—č–≤–į—ā—Ć —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ķ, —Ö–ł–ľ–ł—á–Ķ—Ā–ļ–ł–Ķ, –Ī–ł–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł–Ķ, —Ź–ī–Ķ—Ä–Ĺ—č–Ķ, –ļ–ĺ—Ā–ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –ł –ī—Ä—É–≥–ł–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā—č. –í —Ā–≤—Ź–∑–ł —Ā —ć—ā–ł–ľ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –Ņ—Ä–ł–ĺ–Ī—Ä–Ķ–Ľ–į –Ī–ĺ–Ľ–Ķ–Ķ –ĺ–Ī—Č–ł–Ļ, —Ą–ĺ—Ä–ľ–į–Ľ–ł–∑–ĺ–≤–į–Ĺ–Ĺ—č–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä, –ł, –ļ–į–ļ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ, –ľ–Ķ–Ĺ–Ķ–Ķ –ī–ĺ—Ā—ā—É–Ņ–Ĺ—č–Ļ –ī–Ľ—Ź —ą–ł—Ä–ĺ–ļ–ĺ–≥–ĺ –ļ—Ä—É–≥–į —á–ł—ā–į—ā–Ķ–Ľ–Ķ–Ļ. –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ —Ā–Ľ–ĺ–∂–Ĺ—č–ľ, –∑–į–Ņ—É—ā–į–Ĺ–Ĺ—č–ľ –ł –ī–ł—Ā–ļ—É—Ā—Ā–ł–ĺ–Ĺ–Ĺ—č–ľ –≤–ĺ–Ņ—Ä–ĺ—Ā–ĺ–ľ. –≠—ā–ĺ –ĺ–Ī—É—Ā–Ľ–ĺ–≤–Ľ–Ķ–Ĺ–ĺ, —Ā –ĺ–ī–Ĺ–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č, —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć—é —Ā–ĺ–ī–Ķ—Ä–∂–į–Ĺ–ł—Ź —Ā–į–ľ–ĺ–≥–ĺ –ĺ–Ī—ä–Ķ–ļ—ā–į –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź ‚ÄĒ —Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ, –ĺ–Ī—Ä–į–∑—É—é—Č–ł—Ö –≤ —Ü–Ķ–Ľ–ĺ–ľ –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—É—é —Ā–ł—Ā—ā–Ķ–ľ—É, –į, —Ā –ī—Ä—É–≥–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č, –ľ–Ĺ–ĺ–≥–ĺ–∑–Ĺ–į—á–Ĺ–ĺ—Ā—ā—Ć—é —ā–Ķ—Ä–ľ–ł–Ĺ–ĺ–≤ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č—Ö –Ņ–ĺ–Ĺ—Ź—ā–ł–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –≤–≤–ĺ–ī–ł–ľ—č—Ö –≤ –ī—Ä—É–≥–ł—Ö —Ä–į–∑–ī–Ķ–Ľ–į—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł —Ā–ľ–Ķ–∂–Ĺ—č—Ö –Ĺ–į—É–ļ–į—Ö –ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ–ľ—č—Ö –Ņ—Ä–ł –ł–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į. [8].
–ė—Ā—ā–ĺ—Ä–ł—Ź –ĺ—ā–ļ—Ä—č—ā–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ĺ–ī–Ĺ—É –ł–∑ —Ā–į–ľ—č—Ö –∑–į–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö, –Ņ–ĺ–Ľ–Ĺ—É—é –ī—Ä–į–ľ–į—ā–ł–∑–ľ–į, –≥–Ľ–į–≤ –ĺ–Ī—Č–Ķ–Ļ –ł—Ā—ā–ĺ—Ä–ł–ł –Ĺ–į—É–ļ–ł, –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł–Ķ —Ā—ā—Ä–į–Ĺ–ł—Ü—č –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ķ—Č—Ď –ī–į–Ľ–Ķ–ļ–ĺ –Ĺ–Ķ –ī–ĺ–Ņ–ł—Ā–į–Ĺ—č. –ü–ĺ—ā—Ä–Ķ–Ī–ĺ–≤–į–Ľ–ł—Ā—Ć —É—Ā–ł–Ľ–ł—Ź –Ĺ–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ, –į –ľ–Ĺ–ĺ–≥–ł—Ö –Ĺ–į—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö –≥–Ķ–Ĺ–ł–Ķ–≤, –ī–Ľ—Ź —ā–ĺ–≥–ĺ —á—ā–ĺ–Ī—č –Ņ—Ä–ł–ĺ—ā–ļ—Ä—č—ā—Ć –∑–į–≤–Ķ—Ā—É –Ĺ–į–ī —Ā–ĺ–ļ—Ä–ĺ–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ —ā–į–Ļ–Ĺ–ĺ–Ļ –Ņ—Ä–ł—Ä–ĺ–ī—č, –ļ–ĺ—ā–ĺ—Ä—É—é –ľ—č –Ĺ–į–∑—č–≤–į–Ķ–ľ —Ā–Ķ–Ļ—á–į—Ā –≤—ā–ĺ—Ä—č–ľ –Ĺ–į—á–į–Ľ–ĺ–ľ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł.[9]
–ė—Ā—Ö–ĺ–ī–Ĺ—č–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –≤–ĺ–∑–Ĺ–ł–ļ–Ľ–ł –≤ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–Ķ –Ņ–ĺ–Ņ—č—ā–ĺ–ļ —Ä–į–∑—Ä–į–Ī–ĺ—ā–ļ–ł –ĺ–Ī—Č–Ķ–Ļ —ā–Ķ–ĺ—Ä–ł–ł [–Ę–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć | —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ–Ļ]. –ü–Ķ—Ä–≤–į—Ź –ī–ĺ–≥–į–ī–ļ–į –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–ł –ĺ—Ā–ĺ–Ī–ĺ–≥–ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—Č–Ķ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —ā–Ķ–Ņ–Ľ–į –≤ —Ä–į–Ī–ĺ—ā—É, –Ī—č–Ľ–į –≤—č—Ā–ļ–į–∑–į–Ĺ–į –°–į–ī–ł –ö–į—Ä–Ĺ–ĺ –≤ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł–ł ¬ę–†–į–∑–ľ—č—ą–Ľ–Ķ–Ĺ–ł–Ķ –ĺ –ī–≤–ł–∂—É—Č–Ķ–Ļ —Ā–ł–Ľ–Ķ –ĺ–≥–Ĺ—Ź –ł –ĺ –ľ–į—ą–ł–Ĺ–į—Ö, —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ—č—Ö —Ä–į–∑–≤–ł–≤–į—ā—Ć —ć—ā—É —Ā–ł–Ľ—ɬĽ (1824 –≥.), –Ĺ–į–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–ľ –ī–ĺ –ĺ—ā–ļ—Ä—č—ā–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā–ł –ł –≤—Ā–Ķ–ĺ–Ī—Č–Ķ–≥–ĺ –Ņ—Ä–ł–∑–Ĺ–į–Ĺ–ł—Ź –∑–į–ļ–ĺ–Ĺ–į —Ā–ĺ—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł—Ź —ć–Ĺ–Ķ—Ä–≥–ł–ł. –í —ć—ā–ĺ–Ļ —Ä–į–Ī–ĺ—ā–Ķ –°–į–ī–ł –ö–į—Ä–Ĺ–ĺ –ł—Ā—Ā–Ľ–Ķ–ī—É–Ķ—ā —É—Ā–Ľ–ĺ–≤–ł—Ź –Ĺ–į–ł–≤—č–≥–ĺ–ī–Ĺ–Ķ–Ļ—ą–Ķ–Ļ —Ä–į–Ī–ĺ—ā—č —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ–Ļ –Ņ—Ä–ł –Ĺ–į–Ľ–ł—á–ł–ł –ī–≤—É—Ö –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–≤ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä: –Ĺ–į–≥—Ä–Ķ–≤–į—ā–Ķ–Ľ—Ź –ł —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ–į (–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–Ĺ–ĺ)[10]. –ě–Ĺ –Ņ—Ä–ł—Ö–ĺ–ī–ł—ā –ļ –≤—č–≤–ĺ–ī—É, —á—ā–ĺ –ľ–į–Ľ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į —ć—ā–ĺ–≥–ĺ —ć—Ą—Ą–Ķ–ļ—ā–į ‚ÄĒ –ļ–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į –Ņ–ĺ–Ľ–Ķ–∑–Ĺ–ĺ–≥–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź (–ö–ü–Ē) ‚ÄĒ –ĺ–Ī—É—Ā–Ľ–į–≤–Ľ–ł–≤–į–Ķ—ā—Ā—Ź –Ĺ–Ķ —ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł–ľ –Ĺ–Ķ—Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ—Ā—ā–≤–ĺ–ľ —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ–Ļ, –į –ĺ—Ā–ĺ–Ī–ĺ–Ļ –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā—Ć—é, –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–ľ, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—Č–ł–ľ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ —ā–Ķ–Ņ–Ľ–į –≤ —Ä–į–Ī–ĺ—ā—É:
–ü—Ä–ł –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ –Ĺ–Ķ–Ľ—Ć–∑—Ź –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –ĺ—ā —ā–Ķ–Ľ–į —ā–Ķ–Ņ–Ľ–ĺ –Ņ—Ä–Ķ–≤—Ä–į—ā–ł—ā—Ć –≤ —Ä–į–Ī–ĺ—ā—É, –Ĺ–Ķ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī—Ź –Ņ—Ä–ł —ć—ā–ĺ–ľ –Ĺ–ł–ļ–į–ļ–ł—Ö –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ļ –≤ —Ā–į–ľ–ĺ–ľ —ā–Ķ–Ľ–Ķ –ł–Ľ–ł –≤ –ī—Ä—É–≥–ł—Ö –ĺ–ļ—Ä—É–∂–į—é—Č–ł—Ö —ā–Ķ–Ľ–į—Ö. [11].
–í —Ā–≤–ĺ–ł—Ö —Ä–į—Ā—Ā—É–∂–ī–Ķ–Ĺ–ł—Ź—Ö –°–į–ī–ł –ö–į—Ä–Ĺ–ĺ —Ä–į–∑–≤–ł–≤–į–Ķ—ā –ł–ī–Ķ—é –ĺ –ļ—Ä—É–≥–ĺ–≤—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į—Ö (—Ü–ł–ļ–Ľ–į—Ö), —Ä–į–∑—Ä–į–Ī–į—ā—č–≤–į–Ķ—ā —Ā—Ö–Ķ–ľ—É —Ü–ł–ļ–Ľ–į, –Ĺ–ĺ—Ā—Ź—Č–Ķ–≥–ĺ –Ķ–≥–ĺ –ł–ľ—Ź, –≤–≤–ĺ–ī–ł—ā –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ –ĺ–Ī –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į—Ö –ł —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä—É–Ķ—ā —ā–Ķ–ĺ—Ä–Ķ–ľ—É –ö–į—Ä–Ĺ–ĺ:
–ö–ü–Ē –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ľ–į—ą–ł–Ĺ –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –≤–ł–ī–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ü–ł–ļ–Ľ–į –ł –Ņ—Ä–ł—Ä–ĺ–ī—č —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ –≤–Ķ—Č–Ķ—Ā—ā–≤–į –ł –≤–Ņ–ĺ–Ľ–Ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ľ–ł—ą—Ć –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –≤–Ĺ–Ķ—ą–Ĺ–ł—Ö –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–≤ ‚ÄĒ –Ĺ–į–≥—Ä–Ķ–≤–į—ā–Ķ–Ľ—Ź ( ) –ł —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ–į (
) –ł —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ–į ( )
)
–°–≤–ĺ–ł –≤—č–≤–ĺ–ī—č –ö–į—Ä–Ĺ–ĺ —Ā–ī–Ķ–Ľ–į–Ľ –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł –ĺ—ą–ł–Ī–ĺ—á–Ĺ–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ—Ä–ĺ–ī–Ĺ–ĺ–Ļ —ā–Ķ–ĺ—Ä–ł–ł –ł –≥–ł–ī—Ä–į–≤–Ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –į–Ĺ–į–Ľ–ĺ–≥–ł–ł. –ü—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź –ĺ —ā–Ķ–Ņ–Ľ–ĺ—Ä–ĺ–ī–Ķ –ļ–į–ļ –ĺ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –Ĺ–Ķ–≤–Ķ—Ā–ĺ–ľ–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ –∂–ł–ī–ļ–ĺ—Ā—ā–ł –Ī—č–Ľ–ł –ĺ–ļ–ĺ–Ĺ—á–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ĺ—Ā—ā–į–≤–Ľ–Ķ–Ĺ—č –≤—Ā–ļ–ĺ—Ä–Ķ –Ņ–ĺ—Ā–Ľ–Ķ –ĺ–Ņ—É–Ī–Ľ–ł–ļ–ĺ–≤–į–Ĺ–ł—Ź —Ä–į–Ī–ĺ—ā—č –ö–į—Ä–Ĺ–ĺ. –†–į–∑–≤–ł–≤–į—Ź –ł–ī–Ķ–ł –ö–į—Ä–Ĺ–ĺ –†. –ö–Ľ–į—É–∑–ł—É—Ā (1850 –≥.) –ł –£. –Ę–ĺ–ľ—Ā–ĺ–Ĺ, (1852 –≥.) —Ā–ĺ–≥–Ľ–į—Ā–ĺ–≤–į–Ľ–ł —ā–Ķ–ĺ—Ä–Ķ–ľ—É –ö–į—Ä–Ĺ–ĺ —Ā –∑–į–ļ–ĺ–Ĺ–ĺ–ľ —Ā–ĺ—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł—Ź —ć–Ĺ–Ķ—Ä–≥–ł–ł; –≤–ľ–Ķ—Ā—ā–Ķ —Ā —ā–Ķ–ľ P. –ö–Ľ–į—É–∑–ł—É—Ā –Ņ–ĺ–Ľ—É—á–ł–Ľ –Ĺ–ĺ–≤—č–Ķ —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā—č, —Ā–ĺ—Ā—ā–į–≤–ł–≤—ą–ł–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–į–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. [12]. –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, —ā–į–ļ –∂–Ķ, –ļ–į–ļ –ł –Ņ–Ķ—Ä–≤–ĺ–Ķ, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ĺ–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ –ĺ–Ī—Č–Ķ—á–Ķ–Ľ–ĺ–≤–Ķ—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ–Ņ—č—ā–į. (–í –ī–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–ľ —Ä–Ķ—á—Ć –Ņ–ĺ–Ļ–ī—Ď—ā –ĺ–Ī ¬ę–ĺ–Ī—č—á–Ĺ—č—Ö¬Ľ, —ā–ĺ –Ķ—Ā—ā—Ć –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ď–Ĺ–Ĺ—č—Ö, —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö, –≤ –ĺ—ā–Ľ–ł—á–ł–Ķ –ĺ—ā —Ä–Ķ–ī–ļ–ĺ –≤—Ā—ā—Ä–Ķ—á–į—é—Č–ł—Ö—Ā—Ź ¬ę–Ĺ–Ķ–ĺ–Ī—č—á–Ĺ—č—Ö¬Ľ —Ā–Ņ–ł–Ĺ–ĺ–≤—č—Ö —Ā–ł—Ā—ā–Ķ–ľ, –ĺ –ļ–ĺ—ā–ĺ—Ä—č—Ö –Ī—É–ī–Ķ—ā —É–Ņ–ĺ–ľ—Ź–Ĺ—É—ā–ĺ –ĺ—ā–ī–Ķ–Ľ—Ć–Ĺ–ĺ).
–ě–Ņ—č—ā –Ņ–ĺ–ļ–į–∑—č–≤–į–Ķ—ā, —á—ā–ĺ —ā–Ķ–Ņ–Ľ–ĺ –ł —Ä–į–Ī–ĺ—ā–į, —Ź–≤–Ľ—Ź—é—Č–ł–Ķ—Ā—Ź, –Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é, —Ą–ĺ—Ä–ľ–į–ľ–ł –Ņ–Ķ—Ä–Ķ–ī–į—á–ł —ć–Ĺ–Ķ—Ä–≥–ł–ł, –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ—Ü–Ķ–Ĺ–Ĺ—č. –ē—Ā–Ľ–ł —Ä–į–Ī–ĺ—ā–į  –ľ–ĺ–∂–Ķ—ā –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā—Ć –≤ —ā–Ķ–Ņ–Ľ–ĺ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ —ā—Ä–Ķ–Ĺ–ł—Ź, –ł –Ņ—Ä–ł —ć—ā–ĺ–ľ –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ľ–į, —ā–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į
–ľ–ĺ–∂–Ķ—ā –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā—Ć –≤ —ā–Ķ–Ņ–Ľ–ĺ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ —ā—Ä–Ķ–Ĺ–ł—Ź, –ł –Ņ—Ä–ł —ć—ā–ĺ–ľ –ł–∑–ľ–Ķ–Ĺ—Ź–Ķ—ā—Ā—Ź —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ľ–į, —ā–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į  —ā–į–ļ–ł–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ –Ĺ–Ķ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā. –ü–ĺ–ī–≤–ĺ–ī —ā–Ķ–Ņ–Ľ–į –Ņ—Ä–ł–≤–ĺ–ī–ł—ā –Ľ–ł—ą—Ć –ļ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł—é –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–Ķ–Ļ —ć–Ĺ–Ķ—Ä–≥–ł–ł —Ā–ł—Ā—ā–Ķ–ľ—č, —ā–ĺ –Ķ—Ā—ā—Ć –ļ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł—é –Ķ—Ď –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤, —ā–į–ļ–ł—Ö –ļ–į–ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į, –ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ, –ĺ–Ī—ä—Ď–ľ –ł —ā. –ī. –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ä–į–Ī–ĺ—ā–į, –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī—Ď–Ĺ–Ĺ–į—Ź –∑–į —Ā—á—Ď—ā –Ņ–Ķ—Ä–Ķ–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į, –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–į –Ľ–ł—ą—Ć –ĺ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –Ņ—É—ā—Ď–ľ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –≤—č—ą–Ķ—É–ļ–į–∑–į–Ĺ–Ĺ—č—Ö –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ä–į–Ī–ĺ—ā–į —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ł—Ź —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į). –ü—Ä–ł —ć—ā–ĺ–ľ, –ļ—Ä–ĺ–ľ–Ķ –ĺ—Ö–Ľ–į–∂–ī–Ķ–Ĺ–ł—Ź —Ā–į–ľ–ĺ–≥–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į —ā–Ķ–Ņ–Ľ–į, –≤ —Ā–Ľ—É—á–į–Ķ –Ĺ–Ķ–∑–į–ľ–ļ–Ĺ—É—ā–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ–≥–ĺ (—Ä–į–Ī–ĺ—á–Ķ–≥–ĺ) —ā–Ķ–Ľ–į, –į –≤ —Ā–Ľ—É—á–į–Ķ –∑–į–ľ–ļ–Ĺ—É—ā–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į ‚ÄĒ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö —ā–Ķ–Ľ, –ļ–ĺ—ā–ĺ—Ä—č–ľ —Ä–į–Ī–ĺ—á–Ķ–Ķ —ā–Ķ–Ľ–ĺ –ī–ĺ–Ľ–∂–Ĺ–ĺ –Ņ–Ķ—Ä–Ķ–ī–į—ā—Ć —á–į—Ā—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–į. –í —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–ľ –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ –Ņ–ĺ–Ľ—É—á–į—ā–Ķ–Ľ–Ķ–ľ —ā–Ķ–Ņ–Ľ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ. –ü—Ä–ĺ—Ü–Ķ—Ā—Ā –ĺ—ā–ī–į—á–ł —á–į—Ā—ā–ł —ā–Ķ–Ņ–Ľ–į –ī—Ä—É–≥–ł–ľ —ā–Ķ–Ľ–į–ľ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–Ķ–Ļ. –ö–į–ļ –Ņ–ĺ–ļ–į–∑—č–≤–į–Ķ—ā –ĺ–Ņ—č—ā, –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–Ķ–≤—Ä–į—ā–ł—ā—Ć —ā–Ķ–Ņ–Ľ–ĺ –≤ —Ä–į–Ī–ĺ—ā—É –Ī–Ķ–∑ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł, —Ź–≤–Ľ—Ź—é—Č–Ķ–Ļ—Ā—Ź —Ü–Ķ–Ĺ–ĺ–Ļ, –ļ–ĺ—ā–ĺ—Ä—É—é –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ ¬ę–∑–į–Ņ–Ľ–į—ā–ł—ā—ƬĽ –∑–į —ć—ā–ĺ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ.
—ā–į–ļ–ł–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ –Ĺ–Ķ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā. –ü–ĺ–ī–≤–ĺ–ī —ā–Ķ–Ņ–Ľ–į –Ņ—Ä–ł–≤–ĺ–ī–ł—ā –Ľ–ł—ą—Ć –ļ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł—é –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–Ķ–Ļ —ć–Ĺ–Ķ—Ä–≥–ł–ł —Ā–ł—Ā—ā–Ķ–ľ—č, —ā–ĺ –Ķ—Ā—ā—Ć –ļ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł—é –Ķ—Ď –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤, —ā–į–ļ–ł—Ö –ļ–į–ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į, –ī–į–≤–Ľ–Ķ–Ĺ–ł–Ķ, –ĺ–Ī—ä—Ď–ľ –ł —ā. –ī. –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ä–į–Ī–ĺ—ā–į, –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī—Ď–Ĺ–Ĺ–į—Ź –∑–į —Ā—á—Ď—ā –Ņ–Ķ—Ä–Ķ–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į, –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–į –Ľ–ł—ą—Ć –ĺ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, –Ņ—É—ā—Ď–ľ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –≤—č—ą–Ķ—É–ļ–į–∑–į–Ĺ–Ĺ—č—Ö –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —Ä–į–Ī–ĺ—ā–į —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ł—Ź —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į). –ü—Ä–ł —ć—ā–ĺ–ľ, –ļ—Ä–ĺ–ľ–Ķ –ĺ—Ö–Ľ–į–∂–ī–Ķ–Ĺ–ł—Ź —Ā–į–ľ–ĺ–≥–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į —ā–Ķ–Ņ–Ľ–į, –≤ —Ā–Ľ—É—á–į–Ķ –Ĺ–Ķ–∑–į–ľ–ļ–Ĺ—É—ā–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ–≥–ĺ (—Ä–į–Ī–ĺ—á–Ķ–≥–ĺ) —ā–Ķ–Ľ–į, –į –≤ —Ā–Ľ—É—á–į–Ķ –∑–į–ľ–ļ–Ĺ—É—ā–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į ‚ÄĒ –Ĺ–Ķ—Ā–ļ–ĺ–Ľ—Ć–ļ–ł—Ö —ā–Ķ–Ľ, –ļ–ĺ—ā–ĺ—Ä—č–ľ —Ä–į–Ī–ĺ—á–Ķ–Ķ —ā–Ķ–Ľ–ĺ –ī–ĺ–Ľ–∂–Ĺ–ĺ –Ņ–Ķ—Ä–Ķ–ī–į—ā—Ć —á–į—Ā—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–į. –í —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–ľ –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ –Ņ–ĺ–Ľ—É—á–į—ā–Ķ–Ľ–Ķ–ľ —ā–Ķ–Ņ–Ľ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ. –ü—Ä–ĺ—Ü–Ķ—Ā—Ā –ĺ—ā–ī–į—á–ł —á–į—Ā—ā–ł —ā–Ķ–Ņ–Ľ–į –ī—Ä—É–≥–ł–ľ —ā–Ķ–Ľ–į–ľ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–Ķ–Ļ. –ö–į–ļ –Ņ–ĺ–ļ–į–∑—č–≤–į–Ķ—ā –ĺ–Ņ—č—ā, –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–Ķ–≤—Ä–į—ā–ł—ā—Ć —ā–Ķ–Ņ–Ľ–ĺ –≤ —Ä–į–Ī–ĺ—ā—É –Ī–Ķ–∑ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł, —Ź–≤–Ľ—Ź—é—Č–Ķ–Ļ—Ā—Ź —Ü–Ķ–Ĺ–ĺ–Ļ, –ļ–ĺ—ā–ĺ—Ä—É—é –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ ¬ę–∑–į–Ņ–Ľ–į—ā–ł—ā—ƬĽ –∑–į —ć—ā–ĺ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ.
–ü–ĺ—Ź—Ā–Ĺ–ł–ľ –Ĺ–į –Ņ—Ä–ł–ľ–Ķ—Ä–Ķ. –†–į–Ī–ĺ—ā–į –≤ —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ź—Ö –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ā—Ź –Ņ—É—ā—Ď–ľ —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ł—Ź —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į. –ß—ā–ĺ–Ī—č —Ā–ī–Ķ–Ľ–į—ā—Ć —Ä–į–Ī–ĺ—ā—É –ľ–į—ą–ł–Ĺ—č –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ļ, —Ä–į–Ī–ĺ—á–Ķ–Ķ —ā–Ķ–Ľ–ĺ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –≤–Ķ—Ä–Ĺ—É—ā—Ć –≤ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –° —ć—ā–ĺ–Ļ —Ü–Ķ–Ľ—Ć—é –Ķ–≥–ĺ –Ĺ–į–ī–ĺ —Ā–∂–į—ā—Ć, –∑–į—ā—Ä–į—ā–ł–≤ —Ä–į–Ī–ĺ—ā—É. –ē—Ā–Ľ–ł —Ā–∂–į—ā–ł–Ķ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć –Ņ—Ä–ł —ā–ĺ–Ļ –∂–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ, —á—ā–ĺ –ł —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ł–Ķ, —ā–ĺ –Ņ–ĺ—ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –∑–į—ā—Ä–į—ā–ł—ā—Ć –≤—Ā—é —Ä–į–Ī–ĺ—ā—É, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ—É—é –Ņ—Ä–ł —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ł–ł, –ł —ć—Ą—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ—Ā—ā—Ć —ć—ā–ĺ–≥–ĺ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ź –Ī—É–ī–Ķ—ā —Ä–į–≤–Ĺ–į –Ĺ—É–Ľ—é. –ß—ā–ĺ–Ī—č —Ä–į–Ī–ĺ—ā–į —Ā–∂–į—ā–ł—Ź –Ī—č–Ľ–į –ľ–Ķ–Ĺ—Ć—ą–Ķ —Ä–į–Ī–ĺ—ā—č —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–ł—Ź, –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć —Ā–∂–į—ā–ł–Ķ –Ņ—Ä–ł –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–ł–∑–ļ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ. –Ē–Ľ—Ź –Ņ–ĺ–Ĺ–ł–∂–Ķ–Ĺ–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į —Ā–Ľ–Ķ–ī—É–Ķ—ā —á–į—Ā—ā—Ć —ā–Ķ–Ņ–Ľ–į –Ņ–Ķ—Ä–Ķ–ī–į—ā—Ć —ā—Ä–Ķ—ā—Ć–Ķ–ľ—É —ā–Ķ–Ľ—É ‚ÄĒ —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ—É.
–ö–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ņ–ĺ–Ľ–Ķ–∑–Ĺ–ĺ–≥–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ź, –Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é, —Ä–į–≤–Ķ–Ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—é –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į, –Ņ—Ä–Ķ–≤—Ä–į—Č—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –≤ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—É—é —Ä–į–Ī–ĺ—ā—É –∑–į –ĺ–ī–ł–Ĺ —Ü–ł–ļ–Ľ, –ļ–ĺ –≤—Ā–Ķ–ľ—É –Ņ–ĺ–ī–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–ľ—É –ļ —Ä–į–Ī–ĺ—á–Ķ–ľ—É —ā–Ķ–Ľ—É –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤—É —ā–Ķ–Ņ–Ľ–į.

–≥–ī–Ķ  ‚ÄĒ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –ĺ—ā –Ĺ–į–≥—Ä–Ķ–≤–į—ā–Ķ–Ľ—Ź,
‚ÄĒ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ–ĺ–Ķ –ĺ—ā –Ĺ–į–≥—Ä–Ķ–≤–į—ā–Ķ–Ľ—Ź,  ‚ÄĒ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –ĺ—ā–ī–į–Ĺ–Ĺ–ĺ–Ķ —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ—É,
‚ÄĒ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –ĺ—ā–ī–į–Ĺ–Ĺ–ĺ–Ķ —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ—É,  ‚ÄĒ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ä–į–Ī–ĺ—ā–į.
‚ÄĒ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ä–į–Ī–ĺ—ā–į.
–ü–Ķ—Ä–≤–ĺ–Ĺ–į—á–į–Ľ—Ć–Ĺ—č–Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –ļ—Ä–į—ā–ļ–į—Ź –ł—Ö —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–į
1.–§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –ö–Ľ–į—É–∑–ł—É—Ā–į (1850).
–Ę–Ķ–Ņ–Ľ–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā—Ć —Ā–į–ľ–ĺ —Ā–ĺ–Ī–ĺ–Ļ –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ď–Ņ–Ľ–ĺ–ľ—É. [13].
–§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –ö–Ľ–į—É–∑–ł—É—Ā–į –Ņ–ĺ–Ľ—É—á–ł–Ľ–į —ą–ł—Ä–ĺ–ļ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –≤ —É—á–Ķ–Ī–Ĺ–ł–ļ–į—Ö —Ą–ł–∑–ł–ļ–ł –ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –Ī–Ľ–į–≥–ĺ–ī–į—Ä—Ź —Ā–≤–ĺ–Ķ–Ļ –Ņ—Ä–ĺ—Ā—ā–ĺ—ā–Ķ –ł –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ—Ā—ā–ł, –ĺ–ī–Ĺ–į–ļ–ĺ —ć—ā–į –Ņ—Ä–ĺ—Ā—ā–ĺ—ā–į –ļ–į–∂—É—Č–į—Ź—Ā—Ź. –Ě–į —Ā–į–ľ–ĺ–ľ –ī–Ķ–Ľ–Ķ –ö–Ľ–į—É–∑–ł—É—Ā –≤ –ī–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–ľ —Ā—Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–į–Ľ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –Ĺ–Ķ–ľ–Ĺ–ĺ–≥–ĺ –ł–Ĺ–į—á–Ķ, —á–Ķ–ľ –Ņ—Ä–ł–≤–Ķ–ī–Ķ–Ĺ–ĺ –≤—č—ą–Ķ, —Ä–į—Ā—ą–ł—Ą—Ä–ĺ–≤–į–≤ —á—ā–ĺŐĀ –ł–ľ–Ķ–Ķ—ā—Ā—Ź –≤ –≤–ł–ī—É –Ņ–ĺ–ī –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ–ľ —Ā–į–ľ–ĺ —Ā–ĺ–Ī–ĺ–Ļ, –ļ–ĺ—ā–ĺ—Ä–ĺ–Ķ –Ĺ–Ķ—Ä–Ķ–ī–ļ–ĺ –ĺ–Ņ—É—Ā–ļ–į–Ķ—ā—Ā—Ź.
–í —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–Ķ –ö–Ľ–į—É–∑–ł—É—Ā–į –ľ–Ĺ–ĺ–≥–ł–Ķ –į–≤—ā–ĺ—Ä—č —É—Ā–ľ–į—ā—Ä–ł–≤–į—é—ā, –≥–Ľ–į–≤–Ĺ—č–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ—ā–≤–Ķ—ā –Ĺ–į –≤–ĺ–Ņ—Ä–ĺ—Ā –ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į –ľ–Ķ–∂–ī—É —ā–Ķ–Ľ–į–ľ–ł –ł–Ľ–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł–ľ–ł —Ā–ł—Ā—ā–Ķ–ľ–į–ľ–ł. –ě–ī–Ĺ–į–ļ–ĺ, –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –Ņ–Ķ—Ä–Ķ–Ĺ–ĺ—Ā–į –≤–Ķ—Č–Ķ—Ā—ā–≤–į, —ć–Ĺ–Ķ—Ä–≥–ł–ł –ł —ā–Ķ–Ņ–Ľ–į —É—Ā—ā–į–Ĺ–į–≤–Ľ–ł–≤–į—é—ā —Ä–į–Ĺ–Ķ–Ķ –ĺ—ā–ļ—Ä—č—ā—č–Ķ –≥—Ä–į–ī–ł–Ķ–Ĺ—ā–Ĺ—č–Ķ –∑–į–ļ–ĺ–Ĺ—č, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł –∑–į–ļ–ĺ–Ĺ –§—É—Ä—Ć–Ķ, –ĺ—ā–Ĺ–ĺ—Ā—Ź—Č–ł–Ļ—Ā—Ź –ļ –Ņ–Ķ—Ä–Ķ–Ĺ–ĺ—Ā—É —ā–Ķ–Ņ–Ľ–į –ĺ—ā –≥–ĺ—Ä—Ź—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į –ļ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–ľ—É. –í —ć—ā–ĺ–ľ —Ā–ľ—č—Ā–Ľ–Ķ –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ –Ĺ–ł—á–Ķ–≥–ĺ –Ĺ–Ķ –ī–ĺ–Ī–į–≤–Ľ—Ź–Ķ—ā –ļ –∑–į–ļ–ĺ–Ĺ—É –§—É—Ä—Ć–Ķ, –ļ—Ä–ĺ–ľ–Ķ —Ā–Ľ–ĺ–≤ —Ā–į–ľ–ĺ —Ā–ĺ–Ī–ĺ–Ļ. –ö–Ľ–į—É–∑–ł—Ā –≤ —Ā–≤–ĺ–ł—Ö —Ā—ā–į—ā—Ć—Ź—Ö –ī–į–Ķ—ā —á—Ď—ā–ļ–ĺ–Ķ —Ä–į–∑—ä—Ź—Ā–Ĺ–Ķ–Ĺ–ł–Ķ —ć—ā–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź. –Ę–Ķ–Ņ–Ľ–ĺ –ľ–ĺ–∂–Ķ—ā –≤ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ—č—Ö —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā—Ć –ĺ—ā —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –≥–ĺ—Ä—Ź—á–Ķ–ľ—É, –Ķ—Ā–Ľ–ł –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā –ī—Ä—É–≥–ĺ–Ļ, –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č–Ļ, –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā –Ņ–Ķ—Ä–Ķ–ī–į—á–ł —ā–Ķ–Ņ–Ľ–į –ł–Ľ–ł —Ä–į–Ī–ĺ—ā—č, –ļ–ĺ—ā–ĺ—Ä—č–Ļ, –Ņ–ĺ —Ā–Ľ–ĺ–≤–į–ľ –ö–Ľ–į—É–∑–ł—É—Ā–į, —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ļ–į–ļ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł—Ź –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–į —ā–Ķ–Ņ–Ľ–į –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ď–Ņ–Ľ–ĺ–ľ—É. –ö–Ľ–į—É–∑–ł—É—Ā –≤ –Ī–ĺ–Ľ–Ķ–Ķ –Ņ–ĺ–∑–ī–Ĺ–ł—Ö —Ä–į–Ī–ĺ—ā–į—Ö —É—ā–ĺ—á–Ĺ—Ź–Ķ—ā —Ā–≤–ĺ—é —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ—É:
–Ę–Ķ–Ņ–Ľ–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā—Ć —Ā–į–ľ–ĺ —Ā–ĺ–Ī–ĺ–Ļ (–Ī–Ķ–∑ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł) –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ď–Ņ–Ľ–ĺ–ľ—É.
–í —ć—ā–ĺ–ľ –ł —Ā–ĺ—Ā—ā–ĺ–ł—ā –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ķ –ĺ—ā–Ľ–ł—á–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ĺ—ā –≥—Ä–į–ī–ł–Ķ–Ĺ—ā–Ĺ—č—Ö –∑–į–ļ–ĺ–Ĺ–ĺ–≤.
2. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į Y. –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į (1851).
–Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł –Ņ–ĺ–ľ–ĺ—Č–ł –Ĺ–Ķ–ĺ–ī—É—ą–Ķ–≤–Ľ—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ľ–į—ā–Ķ—Ä–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –į–≥–Ķ–Ĺ—ā–į –Ņ–ĺ–Ľ—É—á–ł—ā—Ć –ĺ—ā –ļ–į–ļ–ĺ–Ļ-–Ľ–ł–Ī–ĺ –ľ–į—Ā—Ā—č –≤–Ķ—Č–Ķ—Ā—ā–≤–į –ľ–Ķ—Ö–į–Ĺ–ł—á–Ķ—Ā–ļ—É—é —Ä–į–Ī–ĺ—ā—É –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ –ĺ—Ö–Ľ–į–∂–ī–Ķ–Ĺ–ł—Ź –Ķ—Ď –Ĺ–ł–∂–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —Ā–į–ľ–ĺ–≥–ĺ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–≥–ĺ –ł–∑ –ĺ–ļ—Ä—É–∂–į—é—Č–ł—Ö –Ņ—Ä–Ķ–ī–ľ–Ķ—ā–ĺ–≤ [13].
–≠—ā–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –Ņ–Ķ—Ä–Ķ—Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–į–Ľ –ú. –ü–Ľ–į–Ĺ–ļ:
3. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į ‚ĒÄ –ü–Ľ–į–Ĺ–ļ–į (1851 –≥.)
–Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł—ā—Ć –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ķ—Ā–ļ–ł –ī–Ķ–Ļ—Ā—ā–≤—É—é—Č—É—é –ľ–į—ą–ł–Ĺ—É, –≤—Ā—Ď –ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ā–≤–ĺ–ī–ł–Ľ–ĺ—Ā—Ć –Ī—č –ļ –Ņ–ĺ–ī–Ĺ—Ź—ā–ł—é –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –≥—Ä—É–∑–į –ł –ĺ—Ö–Ľ–į–∂–ī–Ķ–Ĺ–ł—é —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į.
–§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į ‚ĒÄ –ü–Ľ–į–Ĺ–ļ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ī–ĺ–Ľ–Ķ–Ķ —á—Ď—ā–ļ–ĺ–Ļ, —á–Ķ–ľ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į, —ā–į–ļ –ļ–į–ļ –≤ —Ä—Ź–ī–Ķ —Ā–Ľ—É—á–į–Ķ–≤ –≤–ĺ–∑–ľ–ĺ–∂–Ķ–Ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź —Ä–į–Ī–ĺ—ā—č –Ņ—Ä–ł –ĺ—Ö–Ľ–į–∂–ī–Ķ–Ĺ–ł–ł –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į —ā–Ķ–Ņ–Ľ–į –Ĺ–ł–∂–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–Ļ —Ā—Ä–Ķ–ī—č. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł –ł–∑ —Ä–Ķ–∑–Ķ—Ä–≤—É–į—Ä–į, –ł–ľ–Ķ—é—Č–Ķ–≥–ĺ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—É –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–Ļ —Ā—Ä–Ķ–ī—č, –≤—č–Ņ—É—Ā—ā–ł—ā—Ć —Ā–∂–į—ā—č–Ļ –≥–į–∑ –Ņ–ĺ–ī –Ņ–ĺ—Ä—ą–Ķ–Ĺ—Ć —Ü–ł–Ľ–ł–Ĺ–ī—Ä–į –ł–Ľ–ł –≤ —Ā–ĺ–Ņ–Ľ–ĺ —ā—É—Ä–Ī–ł–Ĺ—č, —ā–ĺ, —Ä–į—Ā—ą–ł—Ä—Ź—Ź—Ā—Ć, –≥–į–∑ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī—Ď—ā —Ä–į–Ī–ĺ—ā—É, –Ņ—Ä–ł—á—Ď–ľ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ķ–≥–ĺ –Ņ–ĺ–Ĺ–ł–∑–ł—ā—Ā—Ź –ł —Ā—ā–į–Ĺ–Ķ—ā –Ĺ–ł–∂–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–Ļ —Ā—Ä–Ķ–ī—č. –ě–ī–Ĺ–į–ļ–ĺ —ć—ā–ĺ—ā –Ņ—Ä–ł–ľ–Ķ—Ä –Ĺ–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł—ā –≤—ā–ĺ—Ä–ĺ–ľ—É –Ĺ–į—á–į–Ľ—É —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —É–ļ–į–∑–į–Ĺ–Ĺ—č–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–∑–į–ľ–ļ–Ĺ—É—ā—č–ľ, –ł, –Ķ—Ā–Ľ–ł –Ķ–≥–ĺ –∑–į–ľ–ļ–Ĺ—É—ā—Ć, —ā–ĺ –Ķ—Ā—ā—Ć –Ņ—Ä–ł–≤–Ķ—Ā—ā–ł —Ä–į–Ī–ĺ—á–Ķ–Ķ —ā–Ķ–Ľ–ĺ –≤ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ī–Ľ—Ź –Ņ–ĺ–≤—ā–ĺ—Ä–Ķ–Ĺ–ł—Ź —Ü–ł–ļ–Ľ–į, —ā–ĺ –Ĺ–ł–ļ–į–ļ–ĺ–Ļ –Ņ–ĺ–Ľ–Ķ–∑–Ĺ–ĺ–Ļ —Ä–į–Ī–ĺ—ā—č —ā–į–ļ–ĺ–Ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć –Ĺ–Ķ –Ņ–Ķ—Ä–Ķ–ī–į—Ā—ā. [14]. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–ł –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į, –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į ‚ĒÄ –ü–Ľ–į–Ĺ–ļ–į, –į —ā–į–ļ–∂–Ķ –í–ł–Ľ—Ć–≥–Ķ–Ľ—Ć–ľ–į –ě—Ā—ā–≤–į–Ľ—Ć–ī–į –Ņ–ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É —Ā–≤–ĺ–ī—Ź—ā—Ā—Ź –ļ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—é –ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā–ĺ–∑–ī–į–Ĺ–ł—Ź –≤–Ķ—á–Ĺ–ĺ–≥–ĺ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į, —ā–ĺ –Ķ—Ā—ā—Ć –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ (—Ü–ł–ļ–Ľ–ł—á–Ķ—Ā–ļ–ł) –ī–Ķ–Ļ—Ā—ā–≤—É—é—Č–Ķ–Ļ –ł–∑–ĺ—ā–Ķ—Ä–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ –ľ–į—ą–ł–Ĺ—č, —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ–Ļ —Ä–į–Ī–ĺ—ā–į—ā—Ć –ĺ—ā –ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ —Ä–Ķ–∑–Ķ—Ä–≤—É–į—Ä–į (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ĺ–ļ–Ķ–į–Ĺ–į) –ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤—č–≤–į—ā—Ć –≤ —Ä–į–Ī–ĺ—ā—É –≤—Ā—é —ć–Ĺ–Ķ—Ä–≥–ł—é, –ł–∑–≤–Ľ–Ķ–ļ–į–Ķ–ľ—É—é –ł–∑ –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–Ļ —Ā—Ä–Ķ–ī—č, –ł–ľ–Ķ—é—Č–Ķ–Ļ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ—É—é —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—É [15], [13], [16].
–°—É—Č–Ķ—Ā—ā–≤—É—é—ā –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā–ł —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ĺ–ļ –ö–Ľ–į—É–∑–ł—É—Ā–į –ł –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į ‚ĒÄ –ü–Ľ–į–Ĺ–ļ–į. [17]. –ě–ī–Ĺ–į–ļ–ĺ, —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—Ā—ā—Ć —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ĺ–ļ –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –ö–Ľ–į—É–∑–ł—É—Ā–į –ĺ—ā–Ľ–ł—á–į–Ķ—ā—Ā—Ź –ĺ—ā —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ĺ–ļ –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į –ł –ü–Ľ–į–Ĺ–ļ–į —ā–Ķ–ľ, —á—ā–ĺ –ĺ–Ĺ–į –Ĺ–Ķ —Ā–≤—Ź–∑–į–Ĺ–į —Ā —Ä–į–Ī–ĺ—ā–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ–Ļ (—Ü–ł–ļ–Ľ–ĺ–ľ). –ü–ĺ—ć—ā–ĺ–ľ—É –ĺ–Ĺ–į –ĺ–Ī–Ľ–į–ī–į–Ķ—ā –Ī–ĺŐĀ–Ľ—Ć—ą–Ķ–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć—é –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā–ł. –ě–Ī–ĺ–Ī—Č–į—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ—É –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į ‚ÄĒ –ü–Ľ–į–Ĺ–ļ–į –Ĺ–į –Ľ—é–Ī—č–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č –ľ–ĺ–∂–Ĺ–ĺ –≤—č—Ä–į–∑–ł—ā—Ć –Ķ—Ď —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
–Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ —É–≤–Ķ–Ľ–ł—á–ł—ā—Ć –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ—Ā—ā—Ć –Ľ—é–Ī–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č (–Ņ–Ķ—Ä–Ķ–≤–Ķ—Ā—ā–ł –Ķ—Ď –ł–∑ –Ī–ĺ–Ľ–Ķ–Ķ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –≤ –ľ–Ķ–Ĺ–Ķ–Ķ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–Ķ) –Ī–Ķ–∑ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł [18].
4. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –ü–Ľ–į–Ĺ–ļ–į (1926 –≥.) (–ü–ĺ—Ā—ā—É–Ľ–į—ā –ú. –ü–Ľ–į–Ĺ–ļ–į)
–ě–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ —ā–Ķ–Ņ–Ľ–į –Ņ—É—ā—Ď–ľ —ā—Ä–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ.
–ü–ĺ—Ā—ā—É–Ľ–į—ā –ú. –ü–Ľ–į–Ĺ–ļ–į –≤–Ķ—Ā—Ć–ľ–į –Ľ–į–ļ–ĺ–Ĺ–ł—á–Ķ–Ĺ, –Ĺ–ĺ –≤—Ā—Ď –∂–Ķ –≤ –Ĺ—Ď–ľ, –Ĺ–į—Ä—Ź–ī—É —Ā –ļ–į—ā–Ķ–≥–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ –ĺ—ā—Ä–ł—Ü–į–Ĺ–ł–Ķ–ľ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ–Ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —ā–Ķ–Ņ–Ľ–į –≤ —Ä–į–Ī–ĺ—ā—É, —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā—Ā—Ź –ł —É–ļ–į–∑–į–Ĺ–ł–Ķ –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ–Ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —Ä–į–Ī–ĺ—ā—č –≤ —ā–Ķ–Ņ–Ľ–ĺ –Ņ—É—ā—Ď–ľ —ā—Ä–Ķ–Ĺ–ł—Ź.
–¶–ł–ļ–Ľ –ł —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–Ĺ–ĺ
–Ę–Ķ–Ņ–Ľ–ĺ–≤—č–Ķ –ľ–į—ą–ł–Ĺ—č, –ļ –ļ–ĺ—ā–ĺ—Ä—č–ľ –≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ –ĺ—ā–Ĺ–ĺ—Ā—Ź—ā—Ā—Ź —ā–Ķ–Ņ–Ľ–ĺ–≤—č–Ķ –ī–≤–ł–≥–į—ā–Ķ–Ľ–ł, —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ—č–Ķ –ľ–į—ą–ł–Ĺ—č –ł —ā–Ķ–Ņ–Ľ–ĺ–≤—č–Ķ –Ĺ–į—Ā–ĺ—Ā—č, –ī–Ľ—Ź –ĺ–Ī–Ķ—Ā–Ņ–Ķ—á–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–Ņ—Ä–Ķ—Ä—č–≤–Ĺ–ĺ–Ļ —Ä–į–Ī–ĺ—ā—č –ī–ĺ–Ľ–∂–Ĺ—č —Ä–į–Ī–ĺ—ā–į—ā—Ć –Ņ–ĺ –∑–į–ľ–ļ–Ĺ—É—ā–ĺ–ľ—É –ļ—Ä—É–≥—É (—Ü–ł–ļ–Ľ—É), –Ņ—Ä–ł –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —Ä–į–Ī–ĺ—á–Ķ–Ķ —ā–Ķ–Ľ–ĺ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ –ľ–į—ą–ł–Ĺ—č –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ķ—Ā–ļ–ł –≤–ĺ–∑–≤—Ä–į—Č–į–Ķ—ā—Ā—Ź –≤ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –ě–ī–Ĺ–ł–ľ –ł–∑ –ł–ī–Ķ–į–Ľ–ł–∑–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ü–ł–ļ–Ľ–ĺ–≤ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ –ľ–į—ą–ł–Ĺ—č —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ü–ł–ļ–Ľ, –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ—č–Ļ –°–į–ī–ł –ö–į—Ä–Ĺ–ĺ –ī–Ľ—Ź –į–Ĺ–į–Ľ–ł–∑–į —Ä–į–Ī–ĺ—ā—č —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ľ–į—ą–ł–Ĺ —Ā —Ü–Ķ–Ľ—Ć—é –Ņ–ĺ–≤—č—ą–Ķ–Ĺ–ł—Ź —ć—Ą—Ą–Ķ–ļ—ā–ł–≤–Ĺ–ĺ—Ā—ā–ł –ł—Ö —Ä–į–Ī–ĺ—ā—č.
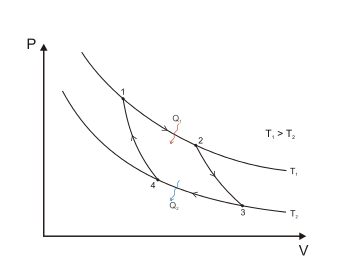 –†–ł—Ā. 1. –¶–ł–ļ–Ľ –ö–į—Ä–Ĺ–ĺ –≤ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į—Ö P –ł V
–†–ł—Ā. 1. –¶–ł–ļ–Ľ –ö–į—Ä–Ĺ–ĺ –≤ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į—Ö P –ł V–Ě–į –ī–ł–į–≥—Ä–į–ľ–ľ–Ķ 1 –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ –ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ —Ü–ł–ļ–Ľ –ö–į—Ä–Ĺ–ĺ –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ—Ď–Ĺ–Ĺ—č–Ļ –ľ–Ķ–∂–ī—É –ī–≤—É–ľ—Ź –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į–ľ–ł —ā–Ķ–Ņ–Ľ–ĺ—ā—č –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č. –ě–Ĺ —Ā–ĺ—Ā—ā–ĺ–ł—ā –ł–∑ –ī–≤—É—Ö –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –ł–∑–ĺ—ā–Ķ—Ä–ľ–ł—á–Ķ—Ā–ļ–ł—Ö (1‚ÄĒ2 –ł 3‚ÄĒ4) –ł –ī–≤—É—Ö –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –į–ī–ł–į–Ī–į—ā–Ĺ—č—Ö (2‚ÄĒ3 –ł 4‚ÄĒ1) –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤. –†–į–Ī–ĺ—á–ł–ľ —ā–Ķ–Ľ–ĺ–ľ —ć—ā–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ –ľ–į—ą–ł–Ĺ—č —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č–Ļ –≥–į–∑. (–ě—Ā–Ĺ–ĺ–≤–Ĺ–į—Ź —Ā—ā–į—ā—Ć—Ź: –¶–ł–ļ–Ľ –ö–į—Ä–Ĺ–ĺ).
–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–Ĺ–ĺ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā, —á—ā–ĺ —ā–Ķ—Ä–ľ–ł—á–Ķ—Ā–ļ–ł–Ļ –ö–ü–Ē –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —Ü–ł–ļ–Ľ–į –ö–į—Ä–Ĺ–ĺ –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –Ņ—Ä–ł—Ä–ĺ–ī—č —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į –ł –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł –Ĺ–į–≥—Ä–Ķ–≤–į—ā–Ķ–Ľ—Ź  –ł —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ–į
–ł —Ö–ĺ–Ľ–ĺ–ī–ł–Ľ—Ć–Ĺ–ł–ļ–į  :
:

–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–Ĺ–ĺ —Ā–ľ. –≤ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ļ —Ā—ā–į—ā—Ć–Ķ: –Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–Ĺ–ĺ (—ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į).
–ė–Ĺ—ā–Ķ–≥—Ä–į–Ľ –ö–Ľ–į—É–∑–ł—É—Ā–į –ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź
–ė–∑ —Ā–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ö–ü–Ē –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —Ü–ł–ļ–Ľ–į –ö–į—Ä–Ĺ–ĺ

–ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ö–ü–Ē –Ľ—é–Ī–ĺ–≥–ĺ —Ü–ł–ļ–Ľ–į

—Ā–Ľ–Ķ–ī—É–Ķ—ā —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ

–ĺ—ā–ļ—É–ī–į, —Ā —É—á—Ď—ā–ĺ–ľ –Ņ—Ä–ł–Ĺ—Ź—ā–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –∑–Ĺ–į–ļ–ĺ–≤: –Ņ–Ľ—é—Ā ‚ĒÄ –ī–Ľ—Ź –Ņ–ĺ–ī–≤–ĺ–ī–ł–ľ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–į –ł –ľ–ł–Ĺ—É—Ā ‚ĒÄ –ī–Ľ—Ź –ĺ—ā–≤–ĺ–ī–ł–ľ–ĺ–≥–ĺ, –Ņ–ĺ–Ľ—É—á–ł–ľ

–ł–Ľ–ł

–ě—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ  –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ—ā–ĺ–Ļ, –į –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–į—Ź —Ā—É–ľ–ľ–į –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č—Ö —ā–Ķ–Ņ–Ľ–ĺ—ā –ī–Ľ—Ź –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —Ü–ł–ļ–Ľ–į –ö–į—Ä–Ĺ–ĺ —Ä–į–≤–Ĺ–į –Ĺ—É–Ľ—é. –Ē–į–Ľ–Ķ–Ķ –ö–Ľ–į—É–∑–ł—É—Ā, —Ä–į–∑–Ī–ł–≤–į–Ķ—ā –į–ī–ł–į–Ī–į—ā–į–ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č–Ļ –ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ —Ü–ł–ļ–Ľ, –Ĺ–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ —á–ł—Ā–Ľ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č—Ö —Ü–ł–ļ–Ľ–ĺ–≤ –ö–į—Ä–Ĺ–ĺ –ł –≤—č–≤–ĺ–ī–ł—ā —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ
–Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ—ā–ĺ–Ļ, –į –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–į—Ź —Ā—É–ľ–ľ–į –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č—Ö —ā–Ķ–Ņ–Ľ–ĺ—ā –ī–Ľ—Ź –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —Ü–ł–ļ–Ľ–į –ö–į—Ä–Ĺ–ĺ —Ä–į–≤–Ĺ–į –Ĺ—É–Ľ—é. –Ē–į–Ľ–Ķ–Ķ –ö–Ľ–į—É–∑–ł—É—Ā, —Ä–į–∑–Ī–ł–≤–į–Ķ—ā –į–ī–ł–į–Ī–į—ā–į–ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č–Ļ –ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ —Ü–ł–ļ–Ľ, –Ĺ–į –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ —á–ł—Ā–Ľ–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ—č—Ö —Ü–ł–ļ–Ľ–ĺ–≤ –ö–į—Ä–Ĺ–ĺ –ł –≤—č–≤–ĺ–ī–ł—ā —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ

–í–≤–Ķ–ī—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ

–Ņ–ĺ–Ľ—É—á–į–Ķ–ľ:

–≠—ā–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ĺ–ľ –ł–Ľ–ł —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ–ľ –ö–Ľ–į—É–∑–ł—É—Ā–į. –ė–Ĺ–ĺ–≥–ī–į –Ķ–≥–ĺ –Ĺ–į–∑—č–≤–į—é—ā –Ņ–Ķ—Ä–≤—č–ľ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ĺ–ľ –ö–Ľ–į—É–∑–ł—É—Ā–į.
–Ę–į–ļ –ļ–į–ļ –Ņ—Ä–ł –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–Ķ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ –ö–Ľ–į—É–∑–ł—É—Ā–į, –≤–∑—Ź—ā—č–Ļ –Ņ–ĺ –ļ–ĺ–Ĺ—ā—É—Ä—É —Ü–ł–ļ–Ľ–į, —Ä–į–≤–Ķ–Ĺ –Ĺ—É–Ľ—é, —ā–ĺ –Ķ–≥–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –Ņ—É—ā–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, –į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –Ľ–ł—ą—Ć –Ĺ–į—á–į–Ľ—Ć–Ĺ—č–ľ –ł –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–ľ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ–ľ —ā–Ķ–Ľ–į. –≠—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā, —á—ā–ĺ –Ņ–ĺ–ī—č–Ĺ—ā–Ķ–≥—Ä–į–Ľ—Ć–Ĺ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ķ—Ā—ā—Ć –Ņ–ĺ–Ľ–Ĺ—č–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł  —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ā–Ķ–Ľ–į (—Ā–ł—Ā—ā–Ķ–ľ—č), –ļ–ĺ—ā–ĺ—Ä—É—é –ö–Ľ–į—É–∑–ł—É—Ā –Ĺ–į–∑–≤–į–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ, —ā–ĺ—á–Ĺ–Ķ–Ķ ‚ÄĒ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ł–Ľ–ł —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ . (–Ē–į–Ľ–Ķ–Ķ, –Ķ—Ā–Ľ–ł –Ĺ–Ķ –ĺ–≥–ĺ–≤–ĺ—Ä–Ķ–Ĺ–ĺ –ĺ—Ā–ĺ–Ī–ĺ, –Ņ–ĺ–ī —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ –Ī—É–ī–Ķ—ā, –ł–ľ–Ķ—ā—Ć—Ā—Ź –≤ –≤–ł–ī—É —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź).
—Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ā–Ķ–Ľ–į (—Ā–ł—Ā—ā–Ķ–ľ—č), –ļ–ĺ—ā–ĺ—Ä—É—é –ö–Ľ–į—É–∑–ł—É—Ā –Ĺ–į–∑–≤–į–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ, —ā–ĺ—á–Ĺ–Ķ–Ķ ‚ÄĒ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ł–Ľ–ł —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ . (–Ē–į–Ľ–Ķ–Ķ, –Ķ—Ā–Ľ–ł –Ĺ–Ķ –ĺ–≥–ĺ–≤–ĺ—Ä–Ķ–Ĺ–ĺ –ĺ—Ā–ĺ–Ī–ĺ, –Ņ–ĺ–ī —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ –Ī—É–ī–Ķ—ā, –ł–ľ–Ķ—ā—Ć—Ā—Ź –≤ –≤–ł–ī—É —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź).
–Ē–Ľ—Ź –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ľ–į–Ľ–ĺ–≥–ĺ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į

–ĺ—ā–ļ—É–ī–į

–Ę–į–ļ –ļ–į–ļ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į  –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ—č–ľ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ĺ–ľ, –į
–Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ—č–ľ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ĺ–ľ, –į  –Ķ—Ā—ā—Ć –Ņ–ĺ–Ľ–Ĺ—č–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ, —ā–ĺ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į
–Ķ—Ā—ā—Ć –Ņ–ĺ–Ľ–Ĺ—č–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ, —ā–ĺ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į  –≤—č—Ā—ā—É–Ņ–į–Ķ—ā –∑–ī–Ķ—Ā—Ć –ļ–į–ļ –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł–Ļ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ć, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ—Ä–Ķ–≤—Ä–į—Č–į–Ķ—ā –Ĺ–Ķ–Ņ–ĺ–Ľ–Ĺ—č–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ
–≤—č—Ā—ā—É–Ņ–į–Ķ—ā –∑–ī–Ķ—Ā—Ć –ļ–į–ļ –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł–Ļ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ć, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ—Ä–Ķ–≤—Ä–į—Č–į–Ķ—ā –Ĺ–Ķ–Ņ–ĺ–Ľ–Ĺ—č–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ  –≤ –Ņ–ĺ–Ľ–Ĺ—č–Ļ.
–í—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ
–≤ –Ņ–ĺ–Ľ–Ĺ—č–Ļ.
–í—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ  –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ī–Ľ—Ź –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –ł–Ľ–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. [19]
–Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ī–Ľ—Ź –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –ł–Ľ–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. [19]
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–Ĺ—č–Ļ –Ĺ–į —Ä–ł—Ā. 2.
 —Ä–ł—Ā.2 –Ě–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā
—Ä–ł—Ā.2 –Ě–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā
–ě–Ĺ —Ā–ĺ—Ā—ā–ĺ–ł—ā –ł–∑ –ī–≤—É—Ö –≤–Ķ—ā–≤–Ķ–Ļ: –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į AIB –ł –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ BIIA, —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —ā–Ķ–Ľ–ĺ –≤–ĺ–∑–≤—Ä–į—Č–į–Ķ—ā—Ā—Ź –≤ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –¶–ł–ļ–Ľ AIBIIA –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ –ł–∑-–∑–į –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į AIB. –ü–Ķ—Ä–≤—č–Ļ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ –ö–Ľ–į—É–∑–ł—É—Ā–į –ľ–ĺ–∂–Ĺ–ĺ –∑–į–Ņ–ł—Ā–į—ā—Ć –≤ –≤–ł–ī–Ķ

–í—ā–ĺ—Ä–ĺ–Ļ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ, –≤–∑—Ź—ā—č–Ļ –Ņ–ĺ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–ľ—É —É—á–į—Ā—ā–ļ—É AIIB, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ —Ä–į–∑–Ĺ–ĺ—Ā—ā—Ć  —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ļ –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–į–ľ–ł A –ł B. –ě—ā—Ā—é–ī–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į –≤ –Ľ—é–Ī–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ
—ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ļ –ľ–Ķ–∂–ī—É —ā–ĺ—á–ļ–į–ľ–ł A –ł B. –ě—ā—Ā—é–ī–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į –≤ –Ľ—é–Ī–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ

–≠—ā–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ľ—É—á–ł–Ľ–ĺ –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–Ļ –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ –ł–Ľ–ł –Ĺ–Ķ—Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ –ö–Ľ–į—É–∑–ł—É—Ā–į.
–í –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–ľ –≤–ł–ī–Ķ:

–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –≤ –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ, –≥–ī–Ķ  (1)
(1)
 (2)
(2)
—ā–ĺ –Ķ—Ā—ā—Ć –≤–ĺ –≤—Ā–Ķ—Ö –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į—Ö —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –Ĺ–Ķ–ł–∑–ľ–Ķ–Ĺ–Ĺ–ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ķ—ā.
–í—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ  –Ķ—Ā—ā—Ć –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ –ł–Ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ī–Ľ—Ź –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤. [20].
–Ķ—Ā—ā—Ć –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ –ł–Ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ī–Ľ—Ź –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤. [20].
–ě–Ī—Č–Ķ–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł
–í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä—É–Ķ—ā—Ā—Ź –ļ–į–ļ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ—Ď–Ĺ–Ĺ—č–Ļ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ. –ė–∑ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź (1) –ł –Ĺ–Ķ—Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į (2) :

–°—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł
–õ. –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ –≤ —Ä–į–Ī–ĺ—ā–Ķ ¬ę–ě —Ā–≤—Ź–∑–ł –ľ–Ķ–∂–ī—É –≤—ā–ĺ—Ä—č–ľ –Ĺ–į—á–į–Ľ–ĺ–ľ –ľ–Ķ—Ö–į–Ĺ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ–ĺ—Ä–ł–ł —ā–Ķ–Ņ–Ľ–ĺ—ā—č –ł —ā–Ķ–ĺ—Ä–ł–Ķ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ķ–Ļ –≤ —ā–Ķ–ĺ—Ä–Ķ–ľ–į—Ö –ĺ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–ľ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł–ł¬Ľ –Ņ–ĺ–ļ–į–∑–į–Ľ —Ā–≤—Ź–∑—Ć –ľ–Ķ–∂–ī—É —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ł–ľ –≤–Ķ—Ā–ĺ–ľ (—ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć—é) –ľ–į–ļ—Ä–ĺ—Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č.[21]
–ó–į–ļ–ĺ–Ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —É –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į –Ņ–ĺ–Ľ—É—á–ł–Ľ –Ņ—Ä–ĺ—Ā—ā—É—é —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ—É—é –ł–Ĺ—ā–Ķ—Ä–Ņ—Ä–Ķ—ā–į—Ü–ł—é: —Ā–ł—Ā—ā–Ķ–ľ–į —Ā—ā—Ä–Ķ–ľ–ł—ā—Ā—Ź –ļ –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ–ľ—É —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—é; —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ –Ņ—Ä–ĺ—ā–Ķ–ļ–į—é—ā —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā—č, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā–ł—Ā—ā–Ķ–ľ–į –ł–∑ –ľ–Ķ–Ĺ–Ķ–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –≤ –Ī–ĺ–Ľ–Ķ–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ–Ķ. –ü—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–į—Ź –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–ĺ–ľ –ł–Ĺ—ā–Ķ—Ä–Ņ—Ä–Ķ—ā–į—Ü–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ļ–į–ļ –ľ–Ķ—Ä—č —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł/–Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –Ĺ–į –į—ā–ĺ–ľ–Ĺ–ĺ-–ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ–ľ —É—Ä–ĺ–≤–Ĺ–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ–ł–Ľ–į –ĺ–Ī–Ĺ–į—Ä—É–∂–ł—ā—Ć —Ä—Ź–ī –≤–į–∂–Ĺ—č—Ö –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–Ķ–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ķ —Ā—ā–į–Ĺ–ĺ–≤—Ź—ā—Ā—Ź –ĺ—á–Ķ–≤–ł–ī–Ĺ—č–ľ–ł, –Ķ—Ā–Ľ–ł –∑–į–ľ–Ķ–Ĺ–ł—ā—Ć —ā–Ķ—Ä–ľ–ł–Ĺ ¬ę—ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź¬Ľ —Ā–Ľ–ĺ–≤–ĺ–ľ ¬ę–Ĺ–Ķ—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—ƬĽ.
–í —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź  —Ā–ł—Ā—ā–Ķ–ľ—č —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ļ–į–ļ —Ą—É–Ĺ–ļ—Ü–ł—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł
—Ā–ł—Ā—ā–Ķ–ľ—č —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ļ–į–ļ —Ą—É–Ĺ–ļ—Ü–ł—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł  –Ķ—Ď —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź (¬ę–Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į¬Ľ).
–Ķ—Ď —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź (¬ę–Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į¬Ľ).

–≥–ī–Ķ  ‚ĒÄ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–į—Ź –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į,
‚ĒÄ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–į—Ź –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į,  ‚ĒÄ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, –ļ–ĺ—ā–ĺ—Ä–į—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ–ľ –ľ–ł–ļ—Ä–ĺ—Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ, —Ä–Ķ–į–Ľ–ł–∑—É—é—Č–ł—Ö –ī–į–Ĺ–Ĺ–ĺ–Ķ –ľ–į–ļ—Ä–ĺ—Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ.
‚ĒÄ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, –ļ–ĺ—ā–ĺ—Ä–į—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ–ľ –ľ–ł–ļ—Ä–ĺ—Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ, —Ä–Ķ–į–Ľ–ł–∑—É—é—Č–ł—Ö –ī–į–Ĺ–Ĺ–ĺ–Ķ –ľ–į–ļ—Ä–ĺ—Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ.
–ó–ī–Ķ—Ā—Ć —Ā–Ľ–Ķ–ī—É–Ķ—ā —Ā–ī–Ķ–Ľ–į—ā—Ć –≤–į–∂–Ĺ–ĺ–Ķ –∑–į–ľ–Ķ—á–į–Ĺ–ł–Ķ. –ó–į –≤—Ä–Ķ–ľ—Ź, –Ņ—Ä–ĺ—ą–Ķ–ī—ą–Ķ–Ķ —Ā –≤–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź, —Ā–ĺ–ī–Ķ—Ä–∂–į–Ĺ–ł–Ķ, –≤–ļ–Ľ–į–ī—č–≤–į–Ķ–ľ–ĺ–Ķ –≤ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –Ķ—Ď –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź –Ņ—Ä–Ķ—ā–Ķ—Ä–Ņ–Ķ–Ľ–ĺ —Ā—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ. –ē—Ā–Ľ–ł –≤–Ĺ–į—á–į–Ľ–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –ĺ—ā–Ĺ–ĺ—Ā–ł–Ľ–ĺ—Ā—Ć –ł—Ā–ļ–Ľ—é—á–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ļ —ā–Ķ–Ņ–Ľ–ĺ–≤—č–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į–ľ, —ā–ĺ –≤ –ī–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–ľ –Ķ–≥–ĺ —Ā—ā–į–Ľ–ł –ĺ–Ī–ĺ–Ī—Č–į—ā—Ć –≤ –ī—Ä—É–≥–ł–Ķ, –Ĺ–Ķ—ā–Ķ–Ņ–Ľ–ĺ–≤—č–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā—č, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –≤ —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ—É—é —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—é –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į –ł –ď–ł–Ī–Ī—Ā–į –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ—É—é —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—é –ļ–į–ļ (–ľ–į–ļ—Ä–ĺ)–≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—Ć —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź. –ü—Ä–ł–ľ–Ķ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ļ —ā–į–ļ–ĺ–ľ—É —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–Ĺ–ĺ–ľ—É –Ņ–ĺ–Ĺ—Ź—ā–ł—é —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –∑–į–ļ–ĺ–Ĺ –Ķ—Ď –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź –Ņ—Ä–ł–ĺ–Ī—Ä–Ķ—ā–į–Ķ—ā —Ą–ĺ—Ä–ľ—É –∑–į–ļ–ĺ–Ĺ–į –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –ē—Ā–Ľ–ł –Ĺ–Ķ —É—á–ł—ā—č–≤–į—ā—Ć –ĺ –ļ–į–ļ–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–ī—Ď—ā —Ä–Ķ—á—Ć, —ā–ĺ –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–ł–Ļ—ā–ł –ļ –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–į–Ľ—Ć–Ĺ—č–ľ –≤—č–≤–ĺ–ī–į–ľ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ĺ –Ĺ–Ķ—Ā–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –∑–į–Ņ—Ä–Ķ—ā–į –Ĺ–į –≤–Ķ—á–Ĺ—č–Ķ –ī–≤–ł–≥–į—ā–Ķ–Ľ–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į, —É—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–Ĺ–ĺ–ľ –∑–į–ļ–ĺ–Ĺ–ĺ–ľ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ī–Ľ—Ź –ĺ–Ī—č—á–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ —Ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ. –ě–ī–Ĺ–į–ļ–ĺ, –Ķ—Ā–Ľ–ł —Ā—á–ł—ā–į—ā—Ć —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤—č–ľ –∑–į–ļ–ĺ–Ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź –Ņ–ĺ–Ľ–Ĺ–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, —ā–ĺ —Ā–Ľ–Ķ–ī—É–Ķ—ā –Ņ—Ä–ł–∑–Ĺ–į—ā—Ć –∑–į–ļ–ĺ–Ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–Ķ–ī–Ķ–Ļ—Ā—ā–≤—É—é—Č–ł–ľ –ł, –ļ–į–ļ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ, –Ņ—Ä–ł–∑–Ĺ–į—ā—Ć –∑–į–Ņ—Ä–Ķ—ā –Ĺ–į –≤–Ķ—á–Ĺ—č–Ķ –ī–≤–ł–≥–į—ā–Ķ–Ľ–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į –Ĺ–Ķ–ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ.[22].
–§–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł
–°—Ä–Ķ–ī–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—Č–ł—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č, —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –∑–į–Ĺ–ł–ľ–į–Ķ—ā –ĺ—Ā–ĺ–Ī–ĺ–Ķ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ.
–ė—Ā—Ö–ĺ–ī—Ź –ł–∑ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā—Ä–į–ļ—ā–ĺ–≤–ļ–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ī–į–Ĺ–Ĺ–ĺ–Ļ –ö–Ľ–į—É–∑–ł—É—Ā–ĺ–ľ,  —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į –Ľ—é–Ī–ĺ–≥–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ľ–į–Ľ–ĺ–≥–ĺ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į —Ä–į–≤–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—é –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–į —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ—É—é —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—É. –ė–Ĺ—č–ľ–ł —Ā–Ľ–ĺ–≤–į–ľ–ł, —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ķ—Ā—ā—Ć –ľ–Ķ—Ä–į –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ľ–į–Ľ–ĺ–≥–ĺ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, –į —ā–į–ļ–∂–Ķ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–≥–ĺ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ł–∑–ĺ—ā–Ķ—Ä–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į.
–ö–į–ļ –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–ĺ –≤ –Ņ—Ä–Ķ–į–ľ–Ī—É–Ľ–Ķ, —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ĺ–Ķ –≤—č—ā–Ķ–ļ–į–Ķ—ā –ł–∑ –Ķ—Ď –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –ł –Ĺ–Ķ –Ņ–ĺ–ī–ī–į—Ď—ā—Ā—Ź –Ņ—Ä–ĺ—Ā—ā–ĺ–ľ—É –ł–Ĺ—ā—É–ł—ā–ł–≤–Ĺ–ĺ–ľ—É –≤–ĺ—Ā–Ņ—Ä–ł—Ź—ā–ł—é.
–í —Ā–≤—Ź–∑–ł —Ā —ć—ā–ł–ľ –Ĺ–Ķ–ĺ–ī–Ĺ–ĺ–ļ—Ä–į—ā–Ĺ–ĺ –Ņ—Ä–Ķ–ī–Ņ—Ä–ł–Ĺ–ł–ľ–į–Ľ–ł—Ā—Ć –Ņ–ĺ–Ņ—č—ā–ļ–ł —É—Ź—Ā–Ĺ–ł—ā—Ć —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –Ď—č–Ľ–ł –Ņ–ĺ–Ņ—č—ā–ļ–ł –Ņ–ĺ–ł—Ā–ļ–į –į–Ĺ–į–Ľ–ĺ–≥–ł–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā –Ī–ĺ–Ľ–Ķ–Ķ –ī–ĺ—Ā—ā—É–Ņ–Ĺ—č–ľ–ł –ī–Ľ—Ź –≤–ĺ—Ā–Ņ—Ä–ł—Ź—ā–ł—Ź –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź–ľ–ł. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ —Ā–ł–Ľ—č –Ĺ–į —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ķ –Ņ–Ķ—Ä–Ķ–ľ–Ķ—Č–Ķ–Ĺ–ł–Ķ, —ā–ĺ –į–Ĺ–į–Ľ–ĺ–≥–ĺ–ľ —Ä–į–Ī–ĺ—ā—č –ľ–ĺ–∂–Ķ—ā —Ā–Ľ—É–∂–ł—ā—Ć –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –į–Ĺ–į–Ľ–ĺ–≥–ĺ–ľ —Ā–ł–Ľ—č ‚ÄĒ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į, –į –į–Ĺ–į–Ľ–ĺ–≥–ĺ–ľ –Ņ–Ķ—Ä–Ķ–ľ–Ķ—Č–Ķ–Ĺ–ł—Ź ‚ÄĒ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź. –ě—á–Ķ–≤–ł–ī–Ĺ–ĺ, —á—ā–ĺ –į–Ĺ–į–Ľ–ĺ–≥–ł–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ–≥–ĺ —ā–ł–Ņ–į –Ĺ–ĺ—Ā—Ź—ā –ł—Ā–ļ—É—Ā—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä, –ł –Ņ–ĺ–Ľ—Ć–∑–į –ĺ—ā –Ĺ–ł—Ö –ī–Ľ—Ź –ł–Ĺ—ā–Ķ—Ä–Ņ—Ä–Ķ—ā–į—Ü–ł–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –≤–Ķ—Ā—Ć–ľ–į —Ā–ĺ–ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–į. –Ę–į–ļ–∂–Ķ –Ĺ–Ķ—Ā–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ņ—č—ā–ļ–į –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –į–Ĺ–į–Ľ–ĺ–≥–ł–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā—Ć—é. –°—Ä–į–≤–Ĺ–ł–ľ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ī–Ľ—Ź —É–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —ā–Ķ–Ľ–į:
—Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į –Ľ—é–Ī–ĺ–≥–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ľ–į–Ľ–ĺ–≥–ĺ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į —Ä–į–≤–Ĺ–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—é –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–į —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ—É—é —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—É. –ė–Ĺ—č–ľ–ł —Ā–Ľ–ĺ–≤–į–ľ–ł, —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ķ—Ā—ā—Ć –ľ–Ķ—Ä–į –Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –ľ–į–Ľ–ĺ–≥–ĺ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, –į —ā–į–ļ–∂–Ķ –ī–Ľ—Ź –Ľ—é–Ī–ĺ–≥–ĺ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–≥–ĺ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ł–∑–ĺ—ā–Ķ—Ä–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į.
–ö–į–ļ –ĺ—ā–ľ–Ķ—á–Ķ–Ĺ–ĺ –≤ –Ņ—Ä–Ķ–į–ľ–Ī—É–Ľ–Ķ, —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ĺ–Ķ –≤—č—ā–Ķ–ļ–į–Ķ—ā –ł–∑ –Ķ—Ď –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –ł –Ĺ–Ķ –Ņ–ĺ–ī–ī–į—Ď—ā—Ā—Ź –Ņ—Ä–ĺ—Ā—ā–ĺ–ľ—É –ł–Ĺ—ā—É–ł—ā–ł–≤–Ĺ–ĺ–ľ—É –≤–ĺ—Ā–Ņ—Ä–ł—Ź—ā–ł—é.
–í —Ā–≤—Ź–∑–ł —Ā —ć—ā–ł–ľ –Ĺ–Ķ–ĺ–ī–Ĺ–ĺ–ļ—Ä–į—ā–Ĺ–ĺ –Ņ—Ä–Ķ–ī–Ņ—Ä–ł–Ĺ–ł–ľ–į–Ľ–ł—Ā—Ć –Ņ–ĺ–Ņ—č—ā–ļ–ł —É—Ź—Ā–Ĺ–ł—ā—Ć —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –Ď—č–Ľ–ł –Ņ–ĺ–Ņ—č—ā–ļ–ł –Ņ–ĺ–ł—Ā–ļ–į –į–Ĺ–į–Ľ–ĺ–≥–ł–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā –Ī–ĺ–Ľ–Ķ–Ķ –ī–ĺ—Ā—ā—É–Ņ–Ĺ—č–ľ–ł –ī–Ľ—Ź –≤–ĺ—Ā–Ņ—Ä–ł—Ź—ā–ł—Ź –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź–ľ–ł. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–į—Ź —Ä–į–Ī–ĺ—ā–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ —Ā–ł–Ľ—č –Ĺ–į —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ķ –Ņ–Ķ—Ä–Ķ–ľ–Ķ—Č–Ķ–Ĺ–ł–Ķ, —ā–ĺ –į–Ĺ–į–Ľ–ĺ–≥–ĺ–ľ —Ä–į–Ī–ĺ—ā—č –ľ–ĺ–∂–Ķ—ā —Ā–Ľ—É–∂–ł—ā—Ć –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –į–Ĺ–į–Ľ–ĺ–≥–ĺ–ľ —Ā–ł–Ľ—č ‚ÄĒ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į, –į –į–Ĺ–į–Ľ–ĺ–≥–ĺ–ľ –Ņ–Ķ—Ä–Ķ–ľ–Ķ—Č–Ķ–Ĺ–ł—Ź ‚ÄĒ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź. –ě—á–Ķ–≤–ł–ī–Ĺ–ĺ, —á—ā–ĺ –į–Ĺ–į–Ľ–ĺ–≥–ł–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ–≥–ĺ —ā–ł–Ņ–į –Ĺ–ĺ—Ā—Ź—ā –ł—Ā–ļ—É—Ā—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä, –ł –Ņ–ĺ–Ľ—Ć–∑–į –ĺ—ā –Ĺ–ł—Ö –ī–Ľ—Ź –ł–Ĺ—ā–Ķ—Ä–Ņ—Ä–Ķ—ā–į—Ü–ł–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –≤–Ķ—Ā—Ć–ľ–į —Ā–ĺ–ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–į. –Ę–į–ļ–∂–Ķ –Ĺ–Ķ—Ā–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ņ—č—ā–ļ–į –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –į–Ĺ–į–Ľ–ĺ–≥–ł–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā—Ć—é. –°—Ä–į–≤–Ĺ–ł–ľ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ī–Ľ—Ź —É–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —ā–Ķ–Ľ–į:

—Ā –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ–ľ —É–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā–ł:
 .
.
–ü–ĺ–ī–ĺ–Ī–ł–Ķ —ć—ā–ł—Ö –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ļ —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–ł –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤—č—Ö –≤–Ķ–Ľ–ł—á–ł–Ĺ –ł –≤ –ĺ–ī–ł–Ĺ–į–ļ–ĺ–≤–ĺ–Ļ —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā–ł –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –ě–Ī–Ķ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –ĺ—ā–Ĺ–Ķ—Ā—Ď–Ĺ–Ĺ–ĺ–Ķ –ļ –Ķ–ī–ł–Ĺ–ł—Ü–Ķ –ľ–į—Ā—Ā—č –ł –Ķ–ī–ł–Ĺ–ł—Ü–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č. –ě–ī–Ĺ–į–ļ–ĺ, –Ķ—Ā–Ľ–ł –≤ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –≤—Ö–ĺ–ī–ł—ā –≤ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ–ĺ–Ļ —Ą–ĺ—Ä–ľ–Ķ –ł –Ķ—Ď –ľ–ĺ–∂–Ĺ–ĺ –ł–∑–ľ–Ķ—Ä—Ź—ā—Ć –≤ –Ľ—é–Ī–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–Ļ —ą–ļ–į–Ľ–Ķ, —ā–ĺ –≤ —Ą–ĺ—Ä–ľ—É–Ľ–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ą–ł–≥—É—Ä–ł—Ä—É–Ķ—ā –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į  . –í –ĺ—ā–Ľ–ł—á–ł–Ķ –ĺ—ā —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā—Ć –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č (–Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É
. –í –ĺ—ā–Ľ–ł—á–ł–Ķ –ĺ—ā —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā—Ć –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č (–Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É  –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ—č–ľ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ĺ–ľ), –į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, —ā–į–ļ –ļ–į–ļ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā —Ā–Ņ–ĺ—Ā–ĺ–Ī–į –Ņ–Ķ—Ä–Ķ–ī–į—á–ł —ā–Ķ–Ņ–Ľ–į (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ—Ä–ł –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ –ī–į–≤–Ľ–Ķ–Ĺ–ł–ł, –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ –ĺ–Ī—ä—Ď–ľ–Ķ –ł —ā–į–ļ –ī–į–Ľ–Ķ–Ķ). –≠–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –ĺ—ā–Ĺ–Ķ—Ā—Ď–Ĺ–Ĺ–ĺ–Ķ –ļ –Ķ–ī–ł–Ĺ–ł—Ü–Ķ –ľ–į—Ā—Ā—č –ł –Ķ–ī–ł–Ĺ–ł—Ü–Ķ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č
–Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ—č–ľ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ–ĺ–ľ), –į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, —ā–į–ļ –ļ–į–ļ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā —Ā–Ņ–ĺ—Ā–ĺ–Ī–į –Ņ–Ķ—Ä–Ķ–ī–į—á–ł —ā–Ķ–Ņ–Ľ–į (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ņ—Ä–ł –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ –ī–į–≤–Ľ–Ķ–Ĺ–ł–ł, –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–ĺ–ľ –ĺ–Ī—ä—Ď–ľ–Ķ –ł —ā–į–ļ –ī–į–Ľ–Ķ–Ķ). –≠–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į, –ĺ—ā–Ĺ–Ķ—Ā—Ď–Ĺ–Ĺ–ĺ–Ķ –ļ –Ķ–ī–ł–Ĺ–ł—Ü–Ķ –ľ–į—Ā—Ā—č –ł –Ķ–ī–ł–Ĺ–ł—Ü–Ķ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č  . –ě–Ĺ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –ł –ł –Ķ—Ď –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č –≤–Ī–Ľ–ł–∑–ł –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā—Ć —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, –į —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź ‚ÄĒ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ —Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ. –§–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –≤—č—Ä–į–∂–Ķ–Ĺ —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
. –ě–Ĺ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –ł –ł –Ķ—Ď –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č –≤–Ī–Ľ–ł–∑–ł –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —ā–Ķ–Ņ–Ľ–ĺ—Ď–ľ–ļ–ĺ—Ā—ā—Ć —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, –į —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź ‚ÄĒ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ —Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ. –§–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –≤—č—Ä–į–∂–Ķ–Ĺ —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
–§–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –≤—č—Ä–į–∂–Ķ–Ĺ —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ:
–≠–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź (–ĺ—ā–Ĺ–Ķ—Ā—Ď–Ĺ–Ĺ–į—Ź –ļ –Ķ–ī–ł–Ĺ–ł—Ü–Ķ –ľ–į—Ā—Ā—č) –Ķ—Ā—ā—Ć —É–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į , –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ–≥–ĺ –ī–Ľ—Ź —ā–ĺ–≥–ĺ, —á—ā–ĺ–Ī—č –Ņ–ĺ—Ā–Ľ–Ķ –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ł –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į, –∑–į–≤–Ķ—Ä—ą–į—é—Č–Ķ–≥–ĺ—Ā—Ź –Ņ—Ä–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–Ķ–Ļ –Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–ľ—É —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—é, –≤–ĺ–∑–≤—Ä–į—ā–ł—ā—Ć —Ä–į–Ī–ĺ—á–Ķ–Ķ —ā–Ķ–Ľ–ĺ –ĺ–Ī—Ä–į—ā–ł–ľ—č–ľ –Ņ—É—ā—Ď–ľ –≤ —ć—ā–ĺ –Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ.
(–£—Ā–Ľ–ĺ–≤–ł–Ķ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł –Ņ–ĺ–ļ–į–∑—č–≤–į–Ķ—ā, —á—ā–ĺ —Ä–Ķ—á—Ć –ł–ī—Ď—ā –ĺ –ľ–ł–Ĺ–ł–ľ–į–Ľ—Ć–Ĺ–ĺ–ľ —É–ī–Ķ–Ľ—Ć–Ĺ–ĺ–ľ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ —ā–Ķ–Ņ–Ľ–į).
–ě—ā—Ā—é–ī–į –ľ–ĺ–∂–Ĺ–ĺ —Ā–ī–Ķ–Ľ–į—ā—Ć –≤—č–≤–ĺ–ī, —á—ā–ĺ —Ü–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –Ņ–Ķ—Ä–Ķ–ī–į–≤–į–Ķ–ľ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–į —ā–Ķ–ľ –≤—č—ą–Ķ, —á–Ķ–ľ –≤—č—ą–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į, –Ņ—Ä–ł –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —ć—ā–į –Ņ–Ķ—Ä–Ķ–ī–į—á–į –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā. –ü–Ķ—Ä–Ķ–ī–į—á–į —Ä–į–Ī–ĺ—á–Ķ–ľ—É —ā–Ķ–Ľ—É –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į  –Ņ—Ä–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ
–Ņ—Ä–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ  –ĺ–∑–Ĺ–į—á–į–Ķ—ā —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ—É –Ņ–Ķ—Ä–Ķ–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–į
–ĺ–∑–Ĺ–į—á–į–Ķ—ā —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ—É –Ņ–Ķ—Ä–Ķ–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–į  , –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ–≥–ĺ –ī–Ľ—Ź –≤–ĺ–∑–≤—Ä–į—ā–į —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į –≤ –Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –Ě–ĺ —ć—ā–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į –Ņ—Ä–ł –∑–į–ī–į–Ĺ–Ĺ–ĺ–ľ
, –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ–≥–ĺ –ī–Ľ—Ź –≤–ĺ–∑–≤—Ä–į—ā–į —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į –≤ –Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ. –Ě–ĺ —ć—ā–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į –Ņ—Ä–ł –∑–į–ī–į–Ĺ–Ĺ–ĺ–ľ  –Ī—É–ī–Ķ—ā —ā–Ķ–ľ –ľ–Ķ–Ĺ—Ć—ą–Ķ, —á–Ķ–ľ –≤—č—ą–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į
–Ī—É–ī–Ķ—ā —ā–Ķ–ľ –ľ–Ķ–Ĺ—Ć—ą–Ķ, —á–Ķ–ľ –≤—č—ą–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į  . –ě—ā—Ā—é–ī–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –Ņ—Ä–ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č
. –ě—ā—Ā—é–ī–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –Ņ—Ä–ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č  —É–ľ–Ķ–Ĺ—Ć—ą–į–Ķ—ā—Ā—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į
—É–ľ–Ķ–Ĺ—Ć—ą–į–Ķ—ā—Ā—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į  –ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į –Ņ—Ä–Ķ–≤—Ä–į—Č–į–Ķ–ľ–ĺ–≥–ĺ –≤ —Ä–į–Ī–ĺ—ā—É, —ā–ĺ –Ķ—Ā—ā—Ć
–ł, —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–į –Ņ—Ä–Ķ–≤—Ä–į—Č–į–Ķ–ľ–ĺ–≥–ĺ –≤ —Ä–į–Ī–ĺ—ā—É, —ā–ĺ –Ķ—Ā—ā—Ć  —É–≤–Ķ–Ľ–ł—á–ł–≤–į–Ķ—ā—Ā—Ź, —á—ā–ĺ , –≤ —Ā–≤–ĺ—é –ĺ—á–Ķ—Ä–Ķ–ī—Ć, –Ņ—Ä–ĺ—Ź—Ā–Ĺ—Ź–Ķ—ā —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ļ–į–ļ –ľ–Ķ—Ä—č –ĺ—Ü–Ķ–Ĺ–ļ–ł –ļ–į—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į –≤ –Ņ–Ľ–į–Ĺ–Ķ –Ķ–≥–ĺ –Ņ—Ä–ł–≥–ĺ–ī–Ĺ–ĺ—Ā—ā–ł –ļ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—é –≤ —Ä–į–Ī–ĺ—ā—É. [23].
—É–≤–Ķ–Ľ–ł—á–ł–≤–į–Ķ—ā—Ā—Ź, —á—ā–ĺ , –≤ —Ā–≤–ĺ—é –ĺ—á–Ķ—Ä–Ķ–ī—Ć, –Ņ—Ä–ĺ—Ź—Ā–Ĺ—Ź–Ķ—ā —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–ľ—č—Ā–Ľ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ļ–į–ļ –ľ–Ķ—Ä—č –ĺ—Ü–Ķ–Ĺ–ļ–ł –ļ–į—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į –≤ –Ņ–Ľ–į–Ĺ–Ķ –Ķ–≥–ĺ –Ņ—Ä–ł–≥–ĺ–ī–Ĺ–ĺ—Ā—ā–ł –ļ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—é –≤ —Ä–į–Ī–ĺ—ā—É. [23].
–° —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ł —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą—Ā–ļ–ĺ–Ļ —ā–ĺ—á–Ķ–ļ –∑—Ä–Ķ–Ĺ–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É–Ķ—ā —ā–į–ļ–∂–Ķ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ—Ā—ā–ł, –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł, –Ĺ–Ķ–ł–ī–Ķ–į–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł —Ä–Ķ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į. –ü–ĺ–ī–ĺ–Ī–Ĺ–ĺ —ā–ĺ–ľ—É, –ļ–į–ļ —ć–Ĺ–Ķ—Ä–≥–ł—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ—É—é –≤–Ķ–Ľ–ł—á–ł–Ĺ—É, –ļ–ĺ—ā–ĺ—Ä–į—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–ĺ–Ļ –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź, —ā–į–ļ –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź (—ā–ĺ—á–Ĺ–Ķ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł) –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–į –ļ–į–ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, —Ź–≤–Ľ—Ź—é—Č–į—Ź—Ā—Ź –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–ĺ–Ļ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ļ–ĺ–Ķ–≥–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –ľ–į—ā–Ķ—Ä–ł–ł ‚ÄĒ –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ—Ā—ā–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į. [6].
–†–Ķ–≤–ł–∑–ł—Ź –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–Ĺ–ĺ–Ļ –Ī–į–∑—č –ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł
–ö–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ł –ľ–Ķ—ā–ĺ–ī –Ķ–≥–ĺ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–Ľ–ł—Ā—Ć —Ö–ĺ–ī–ĺ–ľ –ł—Ā—ā–ĺ—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –Ě–į –Ņ–Ķ—Ä–≤—č—Ö –Ņ–ĺ—Ä–į—Ö —É—á—Ď–Ĺ—č–Ķ –Ĺ–Ķ –∑–į–ī—É–ľ—č–≤–į–Ľ–ł—Ā—Ć –Ĺ–į–ī —ā–Ķ–ľ, —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ľ–ł –≤ –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–ľ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–ł –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł —Ā—ā–ĺ–Ľ—Ć –∂–Ķ –Ī–Ķ–∑—É–Ņ—Ä–Ķ—á–Ĺ—č–ľ –ļ–į–ļ –ł –Ņ–Ķ—Ä–≤–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ ‚ÄĒ —á–į—Ā—ā–Ĺ—č–Ļ —Ā–Ľ—É—á–į–Ļ –≤—Ā–Ķ–ĺ–Ī—Č–Ķ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į —Ā–ĺ—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł—Ź –ł –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —ć–Ĺ–Ķ—Ä–≥–ł–ł, –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā—Ć –ł —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –Ņ–ĺ—á—ā–ł –Ĺ–ł —É –ļ–ĺ–≥–ĺ –Ĺ–Ķ –≤—č–∑—č–≤–į–Ľ–į —Ā–ĺ–ľ–Ĺ–Ķ–Ĺ–ł–Ļ —É–∂–Ķ –≤ –ļ–ĺ–Ĺ—Ü–Ķ 70-—Ö –≥–ĺ–ī–ĺ–≤ XIX –≤–Ķ–ļ–į. –ü–ĺ–Ĺ—Ź—ā–Ĺ—č–ľ –Ī—č–Ľ–ĺ –∂–Ķ–Ľ–į–Ĺ–ł–Ķ —É—á—Ď–Ĺ—č—Ö –≤–ł–ī–Ķ—ā—Ć —Ā—ā–ĺ–Ľ—Ć –∂–Ķ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ—č–ľ –ł –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā—Ć –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —ā–į–ļ–∂–Ķ –Ī—č–Ľ–į –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –ĺ—á–Ķ–≤–ł–ī–Ĺ–į.
–Ě–į —Ä—É–Ī–Ķ–∂–Ķ XIX ‚ĒÄ XX –≤–Ķ–ļ–ĺ–≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į –≤—č—ą–Ľ–į –∑–į –Ņ—Ä–Ķ–ī–Ķ–Ľ—č –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł —ā–Ķ–Ņ–Ľ–į –ł —Ä–į–Ī–ĺ—ā—č –ł, –≤–ĺ–ĺ–Ī—Č–Ķ, –∑–į —Ä–į–ľ–ļ–ł —Ą–ł–∑–ł–ļ–ł. –°—ā–į–Ľ–ĺ —Ź—Ā–Ĺ–ĺ, —á—ā–ĺ –ĺ–Ī–į –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—č—Ö –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł–Ļ –ľ–Ķ—ā–ĺ–ī, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –ĺ–Ī—Č–ł–Ķ –∑–į–ļ–ĺ–Ĺ—č –Ņ—Ä–ł—Ä–ĺ–ī—č. –Ě–ĺ–≤—č–Ķ —ā–Ķ–ĺ—Ä–ł–ł –ł –≤–ĺ–∑–∑—Ä–Ķ–Ĺ–ł—Ź –≤ –ĺ–Ī–Ľ–į—Ā—ā–ł —Ą–ł–∑–ł–ļ–ł, —Ö–ł–ľ–ł–ł –ł –Ī–ł–ĺ–Ľ–ĺ–≥–ł–ł –ī–ĺ–Ľ–∂–Ĺ—č –Ī—č—ā—Ć —Ā–ĺ–≥–Ľ–į—Ā–ĺ–≤–į–Ĺ—č –Ĺ–Ķ —ā–ĺ–Ľ—Ć–ļ–ĺ —Ā –Ņ–Ķ—Ä–≤—č–ľ, –Ĺ–ĺ –ł —Ā –≤—ā–ĺ—Ä—č–ľ –Ĺ–į—á–į–Ľ–ĺ–ľ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –í–ĺ–∑–Ĺ–ł–ļ–Ľ–į –Ņ–ĺ—ā—Ä–Ķ–Ī–Ĺ–ĺ—Ā—ā—Ć –≤ —Ā—ā—Ä–ĺ–≥–ĺ–ľ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ–ĺ–ľ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–ľ –ľ–Ķ—ā–ĺ–ī–Ķ —Ą–Ķ–Ĺ–ĺ–ľ–Ķ–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ–Ņ–ł—Ā–į–Ĺ–ł—Ź –Ņ—Ä–ł—Ä–ĺ–ī–Ĺ—č—Ö —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ –≤ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –ĺ–Ī–Ľ–į—Ā—ā—Ź—Ö –Ķ—Ā—ā–Ķ—Ā—ā–≤–ĺ–∑–Ĺ–į–Ĺ–ł—Ź, –Ĺ–Ķ –Ņ—Ä–ł–≤—Ź–∑–į–Ĺ–Ĺ–ĺ–ľ –ļ –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ—č–ľ —ā–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–ł–ľ —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź–ľ, —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į–ľ, –≥–ł–Ņ–ĺ—ā–Ķ–∑–į–ľ –ł —ā–Ķ–ĺ—Ä–ł—Ź–ľ –ĺ —Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –≤–Ķ—Č–Ķ—Ā—ā–≤–į. –ö —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į–ľ –ł –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź–ľ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ļ —ć—ā–ĺ–ľ—É –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł –Ĺ–į–ļ–ĺ–Ņ–ł–Ľ–ĺ—Ā—Ć –Ĺ–Ķ–ľ–į–Ľ–ĺ –∑–į–ľ–Ķ—á–į–Ĺ–ł–Ļ:
1. –í–Ņ–Ķ—Ä–≤—č–Ķ –ď–Ķ—Ä–ľ–į–Ĺ –ď–Ķ–Ľ—Ć–ľ–≥–ĺ–Ľ—Ć—Ü (1884) –ĺ–Ī—Ä–į—ā–ł–Ľ –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ –Ĺ–į —ā–ĺ –ĺ–Ī—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ, —á—ā–ĺ –ī–Ľ—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –Ĺ–Ķ—ā –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ—Ä—É–≥–ĺ–≤—č–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā—č –ł –Ņ—Ä–ł–≤–Ľ–Ķ–ļ–į—ā—Ć –≥–ł–Ņ–ĺ—ā–Ķ–∑—É –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –≥–į–∑–į, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ľ—é–Ī–ĺ–≥–ĺ —ā–Ķ–Ľ–į –Ķ—Ā—ā—Ć –Ĺ–Ķ —á—ā–ĺ –ł–Ĺ–ĺ–Ķ, –ļ–į–ļ —ā–ĺ—ā –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł–Ļ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ć –ī–Ľ—Ź —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–≥–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į —ā–Ķ–Ņ–Ľ–į, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –∑–į–≤–ł—Ā–ł—ā –ĺ—ā –ĺ–ī–Ĺ–ĺ–Ļ —ā–ĺ–Ľ—Ć–ļ–ĺ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —ā–Ķ–Ľ–į, –ĺ—ā—Ā—á–ł—ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ –≤—č–Ī—Ä–į–Ĺ–Ĺ–ĺ–Ļ —ą–ļ–į–Ľ–Ķ.
2. –ü–ĺ—Ā—ā—É–Ľ–į—ā—č –ö–Ľ–į—É–∑–ł—É—Ā–į –ł –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä—É—é—ā—Ā—Ź –ļ–į–ļ –ĺ—ā—Ä–ł—Ü–į–Ĺ–ł–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –ļ–į–ļ–ĺ–≥–ĺ-–Ľ–ł–Ī–ĺ —Ź–≤–Ľ–Ķ–Ĺ–ł—Ź, —ā–ĺ –Ķ—Ā—ā—Ć –ļ–į–ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā—č –∑–į–Ņ—Ä–Ķ—Č–Ķ–Ĺ–ł—Ź. –ě–Ĺ–ł —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ –Ĺ–Ķ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—ā —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–ľ —ā—Ä–Ķ–Ī–ĺ–≤–į–Ĺ–ł—Ź–ľ, –Ņ—Ä–Ķ–ī—ä—Ź–≤–Ľ—Ź–Ķ–ľ—č–ľ –ļ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—é –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ļ–į–ļ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ł –Ĺ–Ķ –≤–Ņ–ĺ–Ľ–Ĺ–Ķ —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—ā –∑–į–ī–į—á–Ķ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, —ā–į–ļ –ļ–į–ļ –ĺ–Ĺ–ł –ī–ĺ–Ľ–∂–Ĺ—č —Ā–ĺ–ī–Ķ—Ä–∂–į—ā—Ć –Ņ—Ä—Ź–ľ–ĺ–Ķ —É–ļ–į–∑–į–Ĺ–ł–Ķ –ĺ–Ī –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ–ĺ–Ļ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č—Ö –≤ –Ņ—Ä–ł—Ä–ĺ–ī–Ķ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ, –į –Ĺ–Ķ –ĺ—ā—Ä–ł—Ü–į–Ĺ–ł–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ĺ–≥–ĺ –ł—Ö —ā–Ķ—á–Ķ–Ĺ–ł—Ź. –Ē–Ķ–Ľ–ĺ –≤ —ā–ĺ–ľ, —á—ā–ĺ –ĺ—ā—Ä–ł—Ü–į–Ĺ–ł–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ—ā–Ķ–ļ–į–Ĺ–ł—Ź –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–į —ā–Ķ–Ņ–Ľ–į –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ď–Ņ–Ľ–ĺ–ľ—É –≤–ĺ–≤—Ā–Ķ –Ĺ–Ķ –ĺ–∑–Ĺ–į—á–į–Ķ—ā –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –Ķ–≥–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–į –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ —ā—Ď–Ņ–Ľ–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –Ī–ĺ–Ľ–Ķ–Ķ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–ĺ–ľ—É, —ā–ĺ –Ķ—Ā—ā—Ć –ĺ—ā—Ä–ł—Ü–į–Ĺ–ł–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –ļ–į–ļ–ĺ–≥–ĺ-–Ľ–ł–Ī–ĺ –Ĺ–Ķ—Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į  –Ĺ–Ķ—ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—é –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł –Ĺ–Ķ—Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ĺ–≥–ĺ –∑–Ĺ–į–ļ–į
–Ĺ–Ķ—ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—é –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł –Ĺ–Ķ—Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ĺ–≥–ĺ –∑–Ĺ–į–ļ–į  . [24].
. [24].
3. –ö–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –ľ–Ķ—ā–ĺ–ī –Ķ–≥–ĺ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–Ľ–ł—Ā—Ć —Ö–ĺ–ī–ĺ–ľ –ł—Ā—ā–ĺ—Ä–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –ě–Ĺ–ł —Ā —Ā–į–ľ–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ĺ–Ī—ä–Ķ–ī–ł–Ĺ—Ź–Ľ–ł –ī–≤–į —Ä–į–∑–Ĺ–ĺ—Ä–ĺ–ī–Ĺ—č—Ö –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į: –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł,–Ņ—Ä–ł—á—Ď–ľ —Ä–Ķ—ą–į—é—Č—É—é —Ä–ĺ–Ľ—Ć –≤ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ł–≥—Ä–į–Ľ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł ‚ĒÄ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł [25].
4. –í –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ļ–į–ļ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ľ—Ā—Ź –ľ–Ķ—ā–ĺ–ī –ļ—Ä—É–≥–ĺ–≤—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ķ—Ā–ļ–ł —Ä–į–∑–≤–ł—ā—č–Ļ –ö–į—Ä–Ĺ–ĺ, –į –∑–į—ā–Ķ–ľ —ą–ł—Ä–ĺ–ļ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–Ĺ—č–Ļ –ö–Ľ–į—É–∑–ł—É—Ā–ĺ–ľ –ł –ī—Ä—É–≥–ł–ľ–ł —É—á—Ď–Ĺ—č–ľ–ł. –≠—ā–ĺ –Ĺ–Ķ–ł–∑–Ī–Ķ–∂–Ĺ–ĺ –Ņ—Ä–ł–≤–ĺ–ī–ł—ā –ļ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ—č–ľ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź–ľ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –Ľ–ł—ą—Ć –ī–Ľ—Ź –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤
 . [26], [27].
. [26], [27].
5. –ü–ĺ–Ľ—É—á–ł–≤—ą–Ķ–Ķ —ą–ł—Ä–ĺ–ļ–ĺ–Ķ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–Ĺ–ĺ, –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–ĺ–Ķ –†. –ö–Ľ–į—É–∑–ł—É—Ā–ĺ–ľ, –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā, –Ī—č—ā—Ć –Ņ—Ä–ł–∑–Ĺ–į–Ĺ–ĺ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ—č–ľ, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –≤ —Ā—Ö–Ķ–ľ—É –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–Ĺ–ĺ –≤–Ĺ–Ķ—Ā–Ķ–Ĺ–ĺ –Ľ–ł—ą–Ĺ–Ķ–Ķ —É—Ā–Ľ–ĺ–≤–ł–Ķ: –Ī–ĺ–Ľ–Ķ–Ķ —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ–Ļ, –Ņ–ĺ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—é, –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–Ļ –ľ–į—ą–ł–Ĺ–Ķ –≤ —Ā—Ö–Ķ–ľ–Ķ –ľ–Ķ—Ö–į–Ĺ–ł—á–Ķ—Ā–ļ–ł —Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ—č—Ö –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –ľ–į—ą–ł–Ĺ –Ĺ–Ķ–ł–∑–ľ–Ķ–Ĺ–Ĺ–ĺ –Ņ—Ä–ł–Ņ–ł—Ā—č–≤–į–Ķ—ā—Ā—Ź —Ä–ĺ–Ľ—Ć —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ź, —á—ā–ĺ, –≤ —Ā–ĺ—á–Ķ—ā–į–Ĺ–ł–ł —Ā –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–ľ –ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–≥–ĺ –∑–į–Ņ—Ä–Ķ—Č–Ķ–Ĺ–ł—Ź –ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–į —ā–Ķ–Ņ–Ľ–į –ĺ—ā —ā–Ķ–Ľ –ľ–Ķ–Ĺ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā—č—Ö –ļ –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā—č–ľ, –Ņ—Ä–ł–≤–ĺ–ī–ł—ā –ļ –Ņ—Ä–į–≤–ł–Ľ—Ć–Ĺ–ĺ–ľ—É –≤—č—Ä–į–∂–Ķ–Ĺ–ł—é —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–Ĺ–ĺ. –ě–ī–Ĺ–į–ļ–ĺ, –Ķ—Ā–Ľ–ł –≤ —Ā—Ö–Ķ–ľ–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ļ –ö–Ľ–į—É–∑–ł—É—Ā–į —Ö—É–ī—ą—É—é (–Ņ–ĺ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—é) –ĺ–Ī—Ä–į—ā–ł–ľ—É—é —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į—ā—Ć –ļ–į–ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć, —ā–ĺ –ī–Ľ—Ź –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–Ĺ–ĺ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –≤–≤–Ķ—Ā—ā–ł –Ņ–ĺ—Ā—ā—É–Ľ–į—ā, –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā—É –ö–Ľ–į—É–∑–ł—É—Ā–į [27]. –ö —ā–į–ļ–ĺ–ľ—É –∂–Ķ –≤—č–≤–ĺ–ī—É –Ņ—Ä–ł—ą–Ķ–Ľ –ł –ď—É—Ö–ľ–į–Ĺ –ě–Ĺ –ī–ĺ–ļ–į–∑–į–Ľ —ā–Ķ–ĺ—Ä–Ķ–ľ—É –ö–į—Ä–Ĺ–ĺ, –∑–į–ľ–Ķ–Ĺ–ł–≤ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ö–Ľ–į—É–∑–ł—É—Ā–į –į–Ĺ—ā–ł–Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–ľ. –ó–į–ľ–Ķ–Ĺ–į –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į –ö–Ľ–į—É–∑–ł—É—Ā–į (–ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ļ –Ņ—Ä–Ķ–ī–Ņ–ĺ—Ā—č–Ľ–ļ–ł) –Ķ–≥–ĺ –į–Ĺ—ā–ł—ā–Ķ–∑–ĺ–Ļ –Ĺ–Ķ –ĺ—ā—Ä–į–∂–į–Ķ—ā—Ā—Ź –Ĺ–ł –Ĺ–į —Ā—É—Č–Ķ—Ā—ā–≤–Ķ –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ—č—Ö —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–ĺ–≤, –Ĺ–ł –Ĺ–į —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ķ –ł—Ö –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł—Ź, —á—ā–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é —Ā–ĺ–≤–Ņ–į–ī–į–Ķ—ā —Ā —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ–ľ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź. –í –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ —Ā—á—Ď—ā–Ķ –ď—É—Ö–ľ–į–Ĺ –Ņ—Ä–ł—Ö–ĺ–ī–ł—ā –ļ –≤—č–≤–ĺ–ī—É, —á—ā–ĺ –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–Ĺ–ĺ–Ķ –ö–Ľ–į—É–∑–ł—É—Ā–ĺ–ľ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–Ĺ–ĺ –≤ –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –Ĺ–Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ĺ –Ĺ–į –Ķ–≥–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–Ķ, [28].
6. –ü—Ä–ł –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –†. –ö–Ľ–į—É–∑–ł—É—Ā —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ź–Ķ—ā –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –ö–ü–Ē –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —Ü–ł–ļ–Ľ–į –ö–į—Ä–Ĺ–ĺ –ī–Ľ—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č—Ö –≥–į–∑–ĺ–≤ –Ĺ–į –≤—Ā–Ķ –ĺ–Ī—Ä–į—ā–ł–ľ—č–Ķ —Ü–ł–ļ–Ľ—č —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ľ–į—ą–ł–Ĺ, –Ĺ–Ķ—Ź–≤–Ĺ–ĺ –≤–ļ–Ľ—é—á–į—Ź –≤ —Ā—Ö–Ķ–ľ—É –≤—č–≤–ĺ–ī–ĺ–≤ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č—Ö –≥–į–∑–ĺ–≤, –Ņ–ĺ–ī—á–ł–Ĺ—Ź—é—Č–ł—Ö—Ā—Ź –ļ–į–ļ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é –ö–Ľ–į–Ņ–Ķ–Ļ—Ä–ĺ–Ĺ–į  , —ā–į–ļ –ł –∑–į–ļ–ĺ–Ĺ—É –Ē–∂–ĺ—É–Ľ—Ź
, —ā–į–ļ –ł –∑–į–ļ–ĺ–Ĺ—É –Ē–∂–ĺ—É–Ľ—Ź  . –ě–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ł–ľ–Ķ—é—Č–Ķ–≥–ĺ –≤–Ķ—Ā—Ć–ľ–į –ĺ–Ī—Č–ł–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä, –Ĺ–į –Ī–į–∑–Ķ —Ā—ā–ĺ–Ľ—Ć —Ā–ĺ–ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į, –ļ–į–ļ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č—Ö –≥–į–∑–ĺ–≤, –Ĺ–Ķ–Ľ—Ć–∑—Ź —Ā—á–ł—ā–į—ā—Ć —É–Ī–Ķ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ, —ā–į–ļ –ļ–į–ļ, —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č—Ö –≥–į–∑–ĺ–≤, –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ĺ—á–Ķ–≤–ł–ī–Ĺ—č–ľ, –į –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–Ľ –Ĺ–Ķ –ī–į—é—ā oc–Ĺo–≤a–Ĺ–ł–Ļ, –ī–Ľ—Ź —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ o –≤o–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –≥–į–∑–ĺ–ĺ–Ī—Ä–į–∑–Ĺ—č—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł—Ö –Ņ—Ä–ł –≤—Ā–Ķ—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –∑–į–ļ–ĺ–Ĺ–į–ľ –Ď–ĺ–Ļ–Ľ—Ź –ł –Ē–∂–ĺ—É–Ľ—Ź.
. –ě–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ł–ľ–Ķ—é—Č–Ķ–≥–ĺ –≤–Ķ—Ā—Ć–ľ–į –ĺ–Ī—Č–ł–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä, –Ĺ–į –Ī–į–∑–Ķ —Ā—ā–ĺ–Ľ—Ć —Ā–ĺ–ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į, –ļ–į–ļ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č—Ö –≥–į–∑–ĺ–≤, –Ĺ–Ķ–Ľ—Ć–∑—Ź —Ā—á–ł—ā–į—ā—Ć —É–Ī–Ķ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ, —ā–į–ļ –ļ–į–ļ, —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č—Ö –≥–į–∑–ĺ–≤, –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ĺ—á–Ķ–≤–ł–ī–Ĺ—č–ľ, –į –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–Ľ –Ĺ–Ķ –ī–į—é—ā oc–Ĺo–≤a–Ĺ–ł–Ļ, –ī–Ľ—Ź —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ļ o –≤o–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –≥–į–∑–ĺ–ĺ–Ī—Ä–į–∑–Ĺ—č—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź—é—Č–ł—Ö –Ņ—Ä–ł –≤—Ā–Ķ—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö –Ņ–Ľ–ĺ—ā–Ĺ–ĺ—Ā—ā–ł –∑–į–ļ–ĺ–Ĺ–į–ľ –Ď–ĺ–Ļ–Ľ—Ź –ł –Ē–∂–ĺ—É–Ľ—Ź.
7. –£—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł –ĺ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–ľ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł –ł –ĺ—ā–ļ—Ä—č—ā–ł–Ķ –≤ 1951 –≥. –Ĺ–Ķ–ĺ–Ī—č—á–Ĺ—č—Ö (–ļ–≤–į–Ĺ—ā–ĺ–≤—č—Ö) —Ā–ł—Ā—ā–Ķ–ľ —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł, –Ņ–ĺ—ą–į—ā–Ĺ—É–Ľ–ł –Ī–į–∑–ĺ–≤—č–Ķ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā—č –ö–Ľ–į—É–∑–ł—É—Ā–į, –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į (–ö–Ķ–Ľ—Ć–≤–ł–Ĺ–į) –ł –ü–Ľ–į–Ĺ–ļ–į, –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –ĺ—ā–≤–Ķ—Ä–≥–Ĺ—É–≤ –ĺ–ī–Ĺ–ł, –Ľ–ł–Ī–ĺ –Ĺ–į–Ľ–ĺ–∂–ł–≤ —Ā–Ķ—Ä—Ć—Ď–∑–Ĺ—č–Ķ –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł—Ź –Ĺ–į –ī—Ä—É–≥–ł–Ķ.
–Ě–Ķ—É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ď–Ĺ–Ĺ–ĺ—Ā—ā—Ć —É—á—Ď–Ĺ—č—Ö —Ā—É—Č–Ķ—Ā—ā–≤—É—é—Č–ł–ľ–ł –ľ–Ķ—ā–ĺ–ī–į–ľ–ł –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ł –ł—Ö –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ĺ–Ķ—Ā–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć—é —Ā—ā–į–Ľ–į —Ā—ā–ł–ľ—É–Ľ–ĺ–ľ —Ä–į–∑–≤–ł—ā–ł—Ź –į–ļ—Ā–ł–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ. –ü–ĺ–ī–Ľ–ł–Ĺ–Ĺ–ĺ–Ļ –∂–Ķ –Ņ—Ä–ł—á–ł–Ĺ–ĺ–Ļ —ć—ā–ĺ–Ļ –Ĺ–Ķ—É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ď–Ĺ–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ—Ā–Ľ—É–∂–ł–Ľ —ā–ĺ—ā —Ą–į–ļ—ā, —á—ā–ĺ –ļ 80-–ľ –≥–ĺ–ī–į–ľ XIX –≤. –≤–ĺ–∑–Ĺ–ł–ļ–Ľ–į –Ņ–ĺ—ā—Ä–Ķ–Ī–Ĺ–ĺ—Ā—ā—Ć –≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–ľ –ľ–Ķ—ā–ĺ–ī–Ķ, —Ā–≤–ĺ–Ī–ĺ–ī–Ĺ–ĺ–ľ –ĺ—ā –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł –≤–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ –ĺ –ľ–Ķ—Ö–į–Ĺ–ł–∑–ľ–Ķ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, –≥–ł–Ņ–ĺ—ā–Ķ–∑, —ā—Ä–Ķ–Ī—É—é—Č–ł—Ö –Ņ–ĺ—Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ –ĺ–Ņ—č—ā–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–ł, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –≥–ł–Ņ–ĺ—ā–Ķ–∑ –ł —ā–Ķ–ĺ—Ä–ł–Ļ –ĺ —Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –≤–Ķ—Č–Ķ—Ā—ā–≤–į. –ě–Ĺ –ī–ĺ–Ľ–∂–Ķ–Ĺ –Ī—č—ā—Ć –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –ĺ–Ī—Č–ł–ľ, —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ—č–ľ –ľ–Ķ—ā–ĺ–ī–ĺ–ľ —Ą–Ķ–Ĺ–ĺ–ľ–Ķ–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ–Ņ–ł—Ā–į–Ĺ–ł—Ź —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ –Ņ—Ä–ł—Ä–ĺ–ī—č, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ľ–ĺ–∂–Ĺ–ĺ –Ī—č–Ľ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –ł –≤ –ī—Ä—É–≥–ł—Ö –ĺ–Ī–Ľ–į—Ā—ā—Ź—Ö —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ķ—Ā—ā–Ķ—Ā—ā–≤–ĺ–∑–Ĺ–į–Ĺ–ł—Ź. –°—ā–į–Ľ–ĺ —Ź—Ā–Ĺ–ĺ –ł —ā–ĺ, —á—ā–ĺ –ĺ–Ī–į –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –Ĺ–į –ļ–ĺ—ā–ĺ—Ä—č—Ö –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł–Ļ –ľ–Ķ—ā–ĺ–ī, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –ĺ–Ī—Č–ł–Ķ –∑–į–ļ–ĺ–Ĺ—č –Ņ—Ä–ł—Ä–ĺ–ī—č.
–ź–ļ—Ā–ł–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ –≤ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł.
–í XX –≤–Ķ–ļ–Ķ –Ī–Ľ–į–≥–ĺ–ī–į—Ä—Ź —Ä–į–Ī–ĺ—ā–į–ľ –Ě. –®–ł–Ľ–Ľ–Ķ—Ä–į, –ö. –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, –Ę. –ź. –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–ĺ–Ļ-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā, –ź. –ź. –ď—É—Ö–ľ–į–Ĺ–į, –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź –ł –ī—Ä. –≤ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –Ņ–ĺ—Ź–≤–ł–Ľ–ĺ—Ā—Ć –Ĺ–ĺ–≤–ĺ–Ķ, –į–ļ—Ā–ł–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ. –í—č—Ź—Ā–Ĺ–ł–Ľ–ĺ—Ā—Ć, —á—ā–ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č—Ö –≤ –Ņ—Ä–ł—Ä–ĺ–ī–Ķ —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, –į –ī–Ľ—Ź –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–Ķ —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź –Ĺ–ł —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł—Ź –ļ—Ä—É–≥–ĺ–≤—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, –Ĺ–ł –ī–ĺ–Ņ—É—Č–Ķ–Ĺ–ł—Ź –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–ł –ł–ī–Ķ–į–Ľ—Ć–Ĺ—č—Ö –≥–į–∑–ĺ–≤. [29]. –ź–≤—ā–ĺ—Ä—č –į–ļ—Ā–ł–ĺ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –ł–∑–Ī—Ä–į–Ľ–ł –ī–Ķ–ī—É–ļ—ā–ł–≤–Ĺ—č–Ļ –Ņ—É—ā—Ć, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ—č–Ļ –Ĺ–į –ī–ĺ–Ņ—É—Č–Ķ–Ĺ–ł–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —á–ł—Ā–Ľ–į –ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—č—Ö –ł –Ī–ĺ–Ľ–Ķ–Ķ –ł–Ľ–ł –ľ–Ķ–Ĺ–Ķ–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ—č—Ö –į–ļ—Ā–ł–ĺ–ľ, –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā —ć–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–Ļ –ł –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č –ł –Ĺ–Ķ —Ā–≤—Ź–∑–į–Ĺ–Ĺ—č—Ö —Ā –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ—č–ľ–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä, —ā–Ķ–Ņ–Ľ–ĺ–≤—č–ľ–ł –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į–ľ–ł.
–ú–Ķ—ā–ĺ–ī –®–ł–Ľ–Ľ–Ķ—Ä–į-–ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł
–í 1909 –≥. –ļ—Ä—É–Ņ–Ĺ—č–Ļ –Ĺ–Ķ–ľ–Ķ—Ü–ļ–ł–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –≥—Ä–Ķ—á–Ķ—Ā–ļ–ĺ–≥–ĺ –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–∂–ī–Ķ–Ĺ–ł—Ź –ö–ĺ–Ĺ—Ā—ā–į–Ĺ—ā–ł–Ĺ –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, –į –Ķ—Č—Ď —Ä–į–Ĺ–Ķ–Ķ –Ě. –Ě. –®–ł–Ľ–Ľ–Ķ—Ä –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ľ–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł—Ź —ā–Ķ–Ľ. –≠—ā–į –ł–ī–Ķ—Ź –Ņ–ĺ–Ľ—É—á–ł–Ľ–į –ī–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–Ķ —Ä–į–∑–≤–ł—ā–ł–Ķ –≤ —Ä–į–Ī–ĺ—ā–į—Ö –ö. –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł. –ü–ĺ—Ā—ā—É–Ľ–į—ā –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –≤—č–ī–≤–ł–Ĺ—É—ā –Ĺ–Ķ –Ņ—É—ā—Ď–ľ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł—Ö —Ā–ł—Ā—ā–Ķ–ľ, –į –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–Ķ–Ĺ–ł—Ź –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ļ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į –ļ–į–ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ĺ–≤ (—Ą–ĺ—Ä–ľ –ü—Ą–į—Ą—Ą–į).
–ú–Ķ—ā–ĺ–ī –®–ł–Ľ–Ľ–Ķ—Ä–į ‚ÄĒ –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –Ĺ–Ķ –Ņ–ĺ–Ľ—É—á–ł–Ľ —ą–ł—Ä–ĺ–ļ–ĺ–≥–ĺ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł—Ź –≤ —Ā–≤—Ź–∑–ł —Ā –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ĺ—á–Ĺ–ĺ–Ļ –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ—Ā—ā—Ć—é –ł—Ā—Ö–ĺ–ī–Ĺ—č—Ö –Ņ—Ä–Ķ–ī–Ņ–ĺ—Ā—č–Ľ–ĺ–ļ –ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–ľ–ł –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ź–ľ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ—Ą–ĺ—Ä–ľ–Ľ–Ķ–Ĺ–ł—Ź –≤—č–≤–ĺ–ī–ĺ–≤. –í –ĺ—Ā–Ĺ–ĺ–≤—É –ľ–Ķ—ā–ĺ–ī–į –Ī—č–Ľ –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł:
–í –Ľ—é–Ī–ĺ–Ļ –ĺ–ļ—Ä–Ķ—Ā—ā–Ĺ–ĺ—Ā—ā–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ –∑–į–ī–į–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ł–ľ–Ķ—é—ā—Ā—Ź —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ—č –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č–ľ –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ł–ľ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ–ľ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź [30].
–≠—ā–į –į–ļ—Ā–ł–ĺ–ľ–į –Ņ–ĺ–Ľ—É—á–ł–Ľ–į –≤ –ī–į–Ľ—Ć–Ĺ–Ķ–Ļ—ą–Ķ–ľ –≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–Ķ –Ĺ–į–ł–ľ–Ķ–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ–ĺ—Ā—ā–ł. –°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—é –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, –Ķ—Ā–Ľ–ł –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č–Ļ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ –ü—Ą–į—Ą—Ą–į  –ĺ–Ī–Ľ–į–ī–į–Ķ—ā —ā–Ķ–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ, —á—ā–ĺ –≤ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –Ī–Ľ–ł–∑–ĺ—Ā—ā–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —ā–ĺ—á–ļ–ł —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –ī—Ä—É–≥–ł–Ķ —ā–ĺ—á–ļ–ł, –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ—č–Ķ –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –Ņ–Ķ—Ä–Ķ–ľ–Ķ—Č–Ķ–Ĺ–ł–Ļ –Ņ–ĺ –Ņ—É—ā–ł
–ĺ–Ī–Ľ–į–ī–į–Ķ—ā —ā–Ķ–ľ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ, —á—ā–ĺ –≤ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–Ļ –Ī–Ľ–ł–∑–ĺ—Ā—ā–ł –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ —ā–ĺ—á–ļ–ł —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –ī—Ä—É–≥–ł–Ķ —ā–ĺ—á–ļ–ł, –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ—č–Ķ –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –Ņ–Ķ—Ä–Ķ–ľ–Ķ—Č–Ķ–Ĺ–ł–Ļ –Ņ–ĺ –Ņ—É—ā–ł  , —ā–ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł–Ķ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–ł —ć—ā–ĺ–≥–ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–į –ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź
, —ā–ĺ —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł–Ķ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–ł —ć—ā–ĺ–≥–ĺ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–į –ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź  . (–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł).
. (–Ę–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł).
–ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ļ–ł –ľ–Ķ—ā–ĺ–ī–į –®–ł–Ľ–Ľ–Ķ—Ä–į ‚ÄĒ –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł:
1. –ě—ā—Ā—É—ā—Ā—ā–≤—É–Ķ—ā –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–į—Ź –ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ—Ā—ā—Ć –≤ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–ł –®–ł–Ľ–Ľ–Ķ—Ä–į –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–ł –ł–Ĺ—ā–Ķ–≥—Ä–ł—É—é—Č–ł—Ö –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ļ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ—č —ā–Ķ–Ľ, –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł—Ö—Ā—Ź –≤ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–ľ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł–ł.
2. –ü—Ä–ł –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–Ķ –ĺ—ā –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–≤ –®–ł–Ľ–Ľ–Ķ—Ä–į –ļ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—é –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–ł –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł—Ö –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ļ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į –Ĺ–Ķ—Ź–≤–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ—č –Ņ—Ä–Ķ–ī–Ņ–ĺ—Ā—č–Ľ–ļ–ł, —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ĺ—č–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ł –Ĺ–Ķ —Ź–≤–Ľ—Ź—é—Č–ł–Ķ—Ā—Ź –ĺ—á–Ķ–≤–ł–ī–Ĺ—č–ľ–ł.
3. –ü–ĺ —Ā–Ľ–ĺ–≤–į–ľ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź "‚Ķ –ü–ĺ—Ā—ā—É–Ľ–į—ā—č –Ě. –Ě. –®–ł–Ľ–Ľ–Ķ—Ä–į (őô‚ÄĒőôőôőô), –ī–į–∂–Ķ –Ņ–ĺ—Ā–Ľ–Ķ –≤–Ĺ–Ķ—Ā–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ—č—Ö –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–ł–≤, –Ĺ–Ķ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –ĺ—ā–Ĺ–Ķ—Ā–Ķ–Ĺ—č –ļ –ļ–į—ā–Ķ–≥–ĺ—Ä–ł–ł –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ĺ—á–Ķ–≤–ł–ī–Ĺ—č—Ö –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ, –Ņ—Ä–ł—á—Ď–ľ –ĺ–Ī—Č–Ķ–Ķ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ —ć—ā–ł—Ö –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –Ľ–ł—ą—Ć –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –≤ —Ā–≤—Ź–∑–ł —Ā —á–Ķ–ľ –ł—Ā–ļ–Ľ—é—á–į–Ķ—ā—Ā—Ź –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –Ņ–Ľ–ĺ–ī–ĺ—ā–≤–ĺ—Ä–Ĺ–ĺ–≥–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł—Ź –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–≤ –Ě. –Ě. –®–ł–Ľ–Ľ–Ķ—Ä–į –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ —Ā—Ä–Ķ–ī—Ā—ā–≤ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź —ć—ā–ĺ–≥–ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į."
4.–®–ł–Ľ–Ľ–Ķ—Ä –Ĺ–Ķ—Ź–≤–Ĺ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ľ –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ĺ–Ķ–ĺ—á–Ķ–≤–ł–ī–Ĺ—É—é –Ņ—Ä–Ķ–ī–Ņ–ĺ—Ā—č–Ľ–ļ—É –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–ł –į–ī–ī–ł—ā–ł–≤–Ĺ—č—Ö  —Ą—É–Ĺ–ļ—Ü–ł–Ļ.
—Ą—É–Ĺ–ļ—Ü–ł–Ļ.
–ö—Ä–ł—ā–ł—á–Ķ—Ā–ļ–ł –ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā—É –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ĺ—ā–Ĺ–ĺ—Ā–ł–Ľ—Ā—Ź –ú. –ü–Ľ–į–Ĺ–ļ. –° –Ķ–≥–ĺ —ā–ĺ—á–ļ–ł –∑—Ä–Ķ–Ĺ–ł—Ź ¬ę—Ā–ĺ–ī–Ķ—Ä–∂–į—Č–ł–Ķ—Ā—Ź –≤ –Ĺ—Ď–ľ –≤—č—Ā–ļ–į–∑—č–≤–į–Ĺ–ł–Ķ –Ĺ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ–Ī—Č–Ķ–Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ—č–ľ –ļ –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į–ľ‚Ķ . –Ě–ł–ļ—ā–ĺ –Ķ—Č—Ď –ł –Ĺ–ł–ļ–ĺ–≥–ī–į –Ĺ–Ķ —Ā—ā–į–≤–ł–Ľ –ĺ–Ņ—č—ā–ĺ–≤ —Ā —Ü–Ķ–Ľ—Ć—é –ī–ĺ—Ā—ā–ł–∂–Ķ–Ĺ–ł—Ź –≤—Ā–Ķ—Ö —Ā–ľ–Ķ–∂–Ĺ—č—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ –ļ–į–ļ–ĺ–≥–ĺ-–Ľ–ł–Ī–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ď–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ—É—ā–Ķ–ľ¬Ľ. –°–ł—Ā—ā–Ķ–ľ–Ķ –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ü–Ľ–į–Ĺ–ļ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–≤–ĺ—é —Ā–ł—Ā—ā–Ķ–ľ—É, –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ—É—é –Ĺ–į –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–Ķ: ¬ę–ě–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ —ā–Ķ–Ņ–Ľ–ĺ—ā—č –Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–ĺ–ľ —ā—Ä–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–嬼, –ļ–ĺ—ā–ĺ—Ä—č–ľ, –Ņ–ĺ –Ķ–≥–ĺ –ľ–Ĺ–Ķ–Ĺ–ł—é, –ł—Ā—á–Ķ—Ä–Ņ—č–≤–į–Ķ—ā—Ā—Ź —Ā–ĺ–ī–Ķ—Ä–∂–į–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł.
–ú–Ķ–∂–ī—É —ā–Ķ–ľ, –ľ–Ķ—ā–ĺ–ī –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, –Ņ–ĺ–Ľ—É—á–ł–Ľ –≤—č—Ā–ĺ–ļ—É—é –ĺ—Ü–Ķ–Ĺ–ļ—É –≤ —Ä–į–Ī–ĺ—ā–Ķ –Ę–į—ā—Ć—Ź–Ĺ—č –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–ĺ–Ļ-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā ¬ę–Ě–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā—Ć, –ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –ł –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł¬Ľ (1928 –≥.). –í —Ā–≤–ĺ–Ķ–Ļ –∑–į–ľ–Ķ—á–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ā—ā–į—ā—Ć–Ķ –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–į-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā –Ņ—Ä–ł—ą–Ľ–į –ļ —Ä—Ź–ī—É –≤–į–∂–Ĺ–Ķ–Ļ—ą–ł—Ö –≤—č–≤–ĺ–ī–ĺ–≤, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł:
1. –ě—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–į–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ —ā–ĺ–ľ, —á—ā–ĺ —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–Ķ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ —ā–Ķ–Ņ–Ľ–ĺ—ā—č  , –ļ–ĺ—ā–ĺ—Ä—č–ľ —Ā–ł—Ā—ā–Ķ–ľ–į –ĺ–Ī–ľ–Ķ–Ĺ–ł–≤–į–Ķ—ā—Ā—Ź –≤ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–Ķ, –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ĺ –≤ –≤–ł–ī–Ķ
, –ļ–ĺ—ā–ĺ—Ä—č–ľ —Ā–ł—Ā—ā–Ķ–ľ–į –ĺ–Ī–ľ–Ķ–Ĺ–ł–≤–į–Ķ—ā—Ā—Ź –≤ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–Ķ, –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ĺ –≤ –≤–ł–ī–Ķ  , –≥–ī–Ķ
, –≥–ī–Ķ  ‚ĒÄ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č, –Ĺ–į–∑—č–≤–į–Ķ–ľ–į—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ, –į
‚ĒÄ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č, –Ĺ–į–∑—č–≤–į–Ķ–ľ–į—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ, –į  ‚ĒÄ —Ą—É–Ĺ–ļ—Ü–ł—Ź –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č, –Ņ–ĺ–Ľ—É—á–ł–≤—ą–į—Ź –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –°–į–ľ–ĺ –∂–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ
‚ĒÄ —Ą—É–Ĺ–ļ—Ü–ł—Ź –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č, –Ņ–ĺ–Ľ—É—á–ł–≤—ą–į—Ź –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –°–į–ľ–ĺ –∂–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ  –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł.
–Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł.
2. –ü—Ä–ł–Ĺ—Ü–ł–Ņ–ł–į–Ľ—Ć–Ĺ–ĺ–Ķ –ĺ—ā–Ľ–ł—á–ł–Ķ –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –ĺ—ā —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ —ā–ĺ–ľ, —á—ā–ĺ –≤ —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö –Ĺ–Ķ–ĺ–ī–Ĺ–ĺ—Ä–ĺ–ī–Ĺ–ĺ—Ā—ā–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–Ľ—Ź –≤–Ĺ—É—ā—Ä–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č, –į —ā–į–ļ–∂–Ķ –Ņ–ĺ—ā–Ķ—Ä—Ć —Ä–į–Ī–ĺ—ā—č –≤ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į—Ö –Ĺ–į —ā—Ä–Ķ–Ĺ–ł–Ķ, —Ā–ĺ–Ņ—Ä–ĺ—ā–ł–≤–Ľ–Ķ–Ĺ–ł–Ķ, –≤–ĺ–∑–ľ–ĺ–∂–Ķ–Ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī —Ā–ł—Ā—ā–Ķ–ľ—č –ļ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—é —Ā –ī—Ä—É–≥–ĺ–Ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–Ķ–Ļ –Ī–Ķ–∑ –ĺ–Ī–ľ–Ķ–Ĺ–į —ā–Ķ–Ņ–Ľ–ĺ—ā–ĺ–Ļ —Ā –ĺ–ļ—Ä—É–∂–į—é—Č–Ķ–Ļ —Ā—Ä–Ķ–ī–ĺ–Ļ. (–≠—ā–ĺ—ā –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā –Ņ–ĺ–∑–ī–Ĺ–Ķ–Ķ –≤ —ā—Ä—É–ī–į—Ö –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź –Ņ–ĺ–Ľ—É—á–ł–Ľ –Ĺ–į–∑–≤–į–Ĺ–ł–Ķ ¬ę–≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–Ķ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į¬Ľ –ł–Ľ–ł —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į). –í–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ł–Ļ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ –≤ –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –≤—Ā–Ķ–≥–ī–į –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ –ł —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ–ľ –Ķ–≥–ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź ¬ę–ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ĺ—Ā—ā—ƬĽ.
3. –ě–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–Ķ–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –≤ —Ä–į–≤–Ĺ–ĺ–Ļ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –ľ—č—Ā–Ľ–ł–ľ–ĺ –ł –ļ–į–ļ –Ĺ–Ķ—É–ļ–Ľ–ĺ–Ĺ–Ĺ–ĺ–Ķ –Ķ—Ď –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł–Ķ –ł–Ľ–ł –ļ–į–ļ –Ĺ–Ķ—É–ļ–Ľ–ĺ–Ĺ–Ĺ–ĺ–Ķ —É–Ī—č–≤–į–Ĺ–ł–Ķ. –§–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ—Ä–Ķ–ī–Ņ–ĺ—Ā—č–Ľ–ļ–ł, —ā–į–ļ–ł–Ķ –ļ–į–ļ –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–į—Ź –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ–ĺ—Ā—ā—Ć –ł –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā—Ć —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, –Ĺ–Ķ –≤—č—Ä–į–∂–į—é—ā –Ĺ–ł–ļ–į–ļ–ł—Ö —ā—Ä–Ķ–Ī–ĺ–≤–į–Ĺ–ł–Ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ—Ä–Ķ–ł–ľ—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź —ā–Ķ—á–Ķ–Ĺ–ł—Ź —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤.
4. –Ē–Ľ—Ź —Ā–ĺ–≥–Ľ–į—Ā–ĺ–≤–į–Ĺ–ł—Ź –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–Ĺ—č—Ö –≤—č–≤–ĺ–ī–ĺ–≤ —Ā –ĺ–Ņ—č—ā–Ĺ—č–ľ–ł –ī–į–Ĺ–Ĺ—č–ľ–ł –ī–Ľ—Ź —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –Ņ—Ä–ł–Ĺ—Ź—ā—Ć –Ņ–ĺ—Ā—ā—É–Ľ–į—ā, —Ā—Ą–Ķ—Ä–į –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –≥—Ä–į–Ĺ–ł—Ü–į–ľ–ł –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ–ĺ—Ā—ā–ł —ć—ā–ł—Ö –ī–į–Ĺ–Ĺ—č—Ö. –Ę–į–ļ–ł–ľ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł.
–ź. –ź. –ď—É—Ö–ľ–į–Ĺ, –ĺ—Ü–Ķ–Ĺ–ł–≤–į—Ź —Ä–į–Ī–ĺ—ā—É –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, —Ā—á–ł—ā–į–Ķ—ā, —á—ā–ĺ –ĺ–Ĺ–į –ĺ—ā–Ľ–ł—á–į–Ķ—ā—Ā—Ź —Ą–ĺ—Ä–ľ–į–Ľ—Ć–Ĺ–ĺ–Ļ –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā—ā—Ä–ĺ–≥–ĺ—Ā—ā—Ć—é –ł –Ī–Ķ–∑—É–Ņ—Ä–Ķ—á–Ĺ–ĺ—Ā—ā—Ć—é –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–ł‚Ķ –í–ľ–Ķ—Ā—ā–Ķ —Ā —ā–Ķ–ľ, –≤ —Ā—ā—Ä–Ķ–ľ–Ľ–Ķ–Ĺ–ł–ł –ļ –Ĺ–į–ł–Ī–ĺ–Ľ—Ć—ą–Ķ–Ļ –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā–ł –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –Ņ—Ä–ł–ī–į–Ľ —Ā–≤–ĺ–Ķ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –Ĺ–į—Ā—ā–ĺ–Ľ—Ć–ļ–ĺ –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ—É—é –ł —Ā–Ľ–ĺ–∂–Ĺ—É—é —Ą–ĺ—Ä–ľ—É, —á—ā–ĺ –ĺ–Ĺ–į –ĺ–ļ–į–∑–į–Ľ–į—Ā—Ć —Ą–į–ļ—ā–ł—á–Ķ—Ā–ļ–ł –Ĺ–Ķ–ī–ĺ—Ā—ā—É–Ņ–Ĺ–ĺ–Ļ –ī–Ľ—Ź –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–į —Ą–ł–∑–ł–ļ–ĺ–≤ —ā–ĺ–≥–ĺ –≤—Ä–Ķ–ľ–Ķ–Ĺ–ł. –ě—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ–ĺ—Ā—ā–ł –ď—É—Ö–ľ–į–Ĺ –∑–į–ľ–Ķ—á–į–Ķ—ā, —á—ā–ĺ –ĺ–Ĺ, –ļ–į–ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł–Ļ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ, –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ –≤ –ĺ—Ā–Ĺ–ĺ–≤—É —ā–Ķ–ĺ—Ä–ł–ł, –ł–ľ–Ķ—é—Č–Ķ–Ļ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ, —ā–į–ļ –ļ–į–ļ –Ĺ–Ķ –ĺ–Ī–Ľ–į–ī–į–Ķ—ā —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ–ľ —Ā–į–ľ–ĺ–ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ—Ā—ā–ł. "–í—Ā—Ď –Ņ—Ä–Ķ–ī–Ķ–Ľ—Ć–Ĺ–ĺ —Ź—Ā–Ĺ–ĺ –≤ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–ł –Ņ—Ä–ĺ—Ā—ā–ĺ–Ļ‚Ķ—Ā–ł—Ā—ā–Ķ–ľ—č‚Ķ –Ě–ĺ —ć—ā–į —Ź—Ā–Ĺ–ĺ—Ā—ā—Ć –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é —É—ā—Ä–į—á–ł–≤–į–Ķ—ā—Ā—Ź –≤ –ĺ–Ī—Č–Ķ–ľ —Ā–Ľ—É—á–į–Ķ –≥–Ķ—ā–Ķ—Ä–ĺ–≥–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č, —É—Ā–Ľ–ĺ–∂–Ĺ—Ď–Ĺ–Ĺ–ĺ–Ļ —Ö–ł–ľ–ł—á–Ķ—Ā–ļ–ł–ľ–ł –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź–ľ–ł –ł –ł—Ā–Ņ—č—ā—č–≤–į—é—Č–Ķ–Ļ –≤–ĺ–∑–ī–Ķ–Ļ—Ā—ā–≤–ł–Ķ –≤–Ĺ–Ķ—ą–Ĺ–ł—Ö –Ņ–ĺ–Ľ–Ķ–Ļ"[31]. –ě–Ĺ —ā–į–ļ–∂–Ķ –≥–ĺ–≤–ĺ—Ä–ł—ā –ł –ĺ —ā–ĺ–ľ, –Ĺ–į—Ā–ļ–ĺ–Ľ—Ć–ļ–ĺ –Ņ—Ä–į–≤–į –Ī—č–Ľ–į –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–į-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā, –Ĺ–į—Ā—ā–į–ł–≤–į—Ź –Ĺ–į –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā–ł –Ņ–ĺ–Ľ–Ĺ–ĺ–≥–ĺ –ĺ—ā–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—č —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ĺ—ā –≤—Ā–Ķ–≥–ĺ, —á—ā–ĺ —Ā–≤—Ź–∑–į–Ĺ–ĺ —Ā –ł–ī–Ķ–Ķ–Ļ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤[32]. –ě—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ĺ—Ā–Ĺ–ĺ–≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ď—É—Ö–ľ–į–Ĺ –Ņ–ĺ–Ľ–į–≥–į–Ķ—ā, —á—ā–ĺ "—Ā–į–ľ–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –ĺ—ā–ī–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ—č —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–Ķ—ā. –í–ĺ–Ņ—Ä–ĺ—Ā —Ā–≤–ĺ–ī–ł—ā—Ā—Ź –ļ —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł—é –Ĺ–į —Ā–Ľ—É—á–į–Ļ —ā–Ķ—Ä–ľ–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź –ĺ–Ņ—č—ā–į –ł–∑—É—á–Ķ–Ĺ–ł—Ź –≤—Ā–Ķ—Ö –ī—Ä—É–≥–ł—Ö —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł–Ļ, –∑–į–≤–Ķ—Ä—ą–į—é—Č–ł—Ö—Ā—Ź —É—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ł–Ķ–ľ –Ķ–ī–ł–Ĺ–ĺ–ĺ–Ī—Ä–į–∑–Ĺ–ĺ–≥–ĺ –Ņ–ĺ —Ą–ĺ—Ä–ľ–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –ī–Ľ—Ź —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ĺ–ĺ–≥–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–į –≤–ĺ–∑–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź  –≠—ā–į —ć–ļ—Ā—ā—Ä–į–Ņ–ĺ–Ľ—Ź—Ü–ł—Ź –ī–į—Ď—ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ź—ā—Ć –Ķ—Ď –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –Ņ—Ä–į–≤–ī–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ–Ļ –≥–ł–Ņ–ĺ—ā–Ķ–∑—č –ł —ā–Ķ–ľ —Ā–į–ľ—č–ľ –Ņ–ĺ—Ā—ā—É–Ľ–ł—Ä–ĺ–≤–į—ā—Ć —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –°–Ľ–Ķ–ī—É–Ķ—ā, –ĺ–ī–Ĺ–į–ļ–ĺ, –∑–į–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł –ĺ–Ī—Č–Ķ—á–Ķ–Ľ–ĺ–≤–Ķ—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ–Ņ—č—ā–į —Ā—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ĺ–≥—Ä–į–Ĺ–ł—á–ł–≤–į–Ķ—ā —Ā—Ą–Ķ—Ä—É –Ķ–≥–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź –ļ–į–ļ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī—č.
–≠—ā–į —ć–ļ—Ā—ā—Ä–į–Ņ–ĺ–Ľ—Ź—Ü–ł—Ź –ī–į—Ď—ā –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ź—ā—Ć –Ķ—Ď –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ –Ņ—Ä–į–≤–ī–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ–Ļ –≥–ł–Ņ–ĺ—ā–Ķ–∑—č –ł —ā–Ķ–ľ —Ā–į–ľ—č–ľ –Ņ–ĺ—Ā—ā—É–Ľ–ł—Ä–ĺ–≤–į—ā—Ć —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –°–Ľ–Ķ–ī—É–Ķ—ā, –ĺ–ī–Ĺ–į–ļ–ĺ, –∑–į–ľ–Ķ—ā–ł—ā—Ć, —á—ā–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł –ĺ–Ī—Č–Ķ—á–Ķ–Ľ–ĺ–≤–Ķ—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ–Ņ—č—ā–į —Ā—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ĺ–≥—Ä–į–Ĺ–ł—á–ł–≤–į–Ķ—ā —Ā—Ą–Ķ—Ä—É –Ķ–≥–ĺ –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź –ļ–į–ļ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī—č.
–Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –≤ —Ā–≤–ĺ–Ķ–Ļ –ľ–ĺ–Ĺ–ĺ–≥—Ä–į—Ą–ł–ł "–Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į" –ī–į–Ľ –ī–Ķ—ā–į–Ľ—Ć–Ĺ—č–Ļ –į–Ĺ–į–Ľ–ł–∑ –ľ–Ĺ–ĺ–≥–ĺ—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č—Ö –Ņ–ĺ–Ņ—č—ā–ĺ–ļ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ļ–į–ļ –ĺ–Ī—ä–Ķ–ī–ł–Ĺ—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ –ĺ–ī–Ĺ–ĺ–≥–ĺ –Ľ–ł—ą—Ć –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł. –ě–Ĺ –Ņ–ĺ–ļ–į–∑–į–Ľ, —á—ā–ĺ –Ņ–ĺ–Ņ—č—ā–ļ–ł —ā–į–ļ–ĺ–≥–ĺ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ĺ–Ķ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –ĺ–Ņ—Ä–į–≤–ī–į–Ĺ—č, –≤–ĺ-–Ņ–Ķ—Ä–≤—č—Ö, –Ņ–ĺ—ā–ĺ–ľ—É, —á—ā–ĺ –≤—č–≤–ĺ–ī –ĺ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –Ĺ–Ķ –ł–ľ–Ķ–Ķ—ā –Ĺ–ł–ļ–į–ļ–ĺ–≥–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź –ļ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ –Ņ—Ä–ł—Ä–ĺ–ī—č, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —ć—ā–ł —Ą—É–Ĺ–ļ—Ü–ł–ł —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź –ł–Ľ–ł —É–Ī—č–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ, –≤–ĺ-–≤—ā–ĺ—Ä—č—Ö, —É–ļ–į–∑–į–Ĺ–ł–Ķ –ĺ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č—Ö –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ —Ā–Ĺ–ł–∂–į–Ķ—ā —É—Ä–ĺ–≤–Ķ–Ĺ—Ć –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł, –≤-—ā—Ä–Ķ—ā—Ć–ł—Ö, –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į ‚ÄĒ –ü–Ľ–į–Ĺ–ļ–į –ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ–Ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł—Ź —ā–Ķ–Ņ–Ľ–į –≤ —Ä–į–Ī–ĺ—ā—É –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł—ā —Ä–Ķ–∑—É–Ľ—Ć—ā–į—ā–į–ľ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł–Ļ —Ā–ł—Ā—ā–Ķ–ľ —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ–Ķ–Ĺ–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ–Ķ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ —ā–Ķ–Ņ–Ľ–į –≤ —Ä–į–Ī–ĺ—ā—É, –Ĺ–ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ–Ķ –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł–Ķ —Ä–į–Ī–ĺ—ā—č –≤ —ā–Ķ–Ņ–Ľ–ĺ.
–í—Ā–Ľ–Ķ–ī –∑–į –Ę. –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–ĺ–Ļ-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā, —á—ā–ĺ —Ä–į–∑–Ľ–ł—á–ł–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–į–Ĺ–ł—Ź, —É—Ä–ĺ–≤–Ĺ—Ź –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā–ł –ł —Ā—Ą–Ķ—Ä—č –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–≤ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ –ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ –Ņ–ĺ —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –Ņ—Ä–ł—á–ł–Ĺ–į–ľ:
1. –ė–∑ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –≤—č—ā–Ķ–ļ–į–Ķ—ā —Ä—Ź–ī –≤–į–∂–Ĺ–Ķ–Ļ—ą–ł—Ö –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –ē–≥–ĺ –Ĺ–į—É—á–Ĺ–ĺ–Ķ –ł –Ņ—Ä–į–ļ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ —ā—Ä—É–ī–Ĺ–ĺ –Ņ–Ķ—Ä–Ķ–ĺ—Ü–Ķ–Ĺ–ł—ā—Ć.
2. –ü—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ –Ķ—Ā—ā—Ć —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–ľ —ā–Ķ—á–Ķ–Ĺ–ł–ł –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č—Ö –≤ –Ņ—Ä–ł—Ä–ĺ–ī–Ķ —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ. –≠—ā–ĺ—ā –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –≤ —Ā—É–∂–ī–Ķ–Ĺ–ł—Ź—Ö –ĺ –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł —ā–Ķ—á–Ķ–Ĺ–ł—Ź —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł—Ö –ł —Ö–ł–ľ–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤ –ł –ł–∑ –Ĺ–Ķ–≥–ĺ –≤—č—ā–Ķ–ļ–į—é—ā –≤—Ā–Ķ –Ĺ–Ķ—Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł.
–£. –ė. –§—Ä–į–Ĺ–ļ—Ą—É—Ä—ā –≤ —Ā–≤–ĺ–Ķ–Ļ —Ā—ā–į—ā—Ć–Ķ "–ö –ł—Ā—ā–ĺ—Ä–ł–ł –į–ļ—Ā–ł–ĺ–ľ–į—ā–ł–ļ–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł", –ĺ–Ņ—É–Ī–Ľ–ł–ļ–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ļ –≤ —Ā–Ī–ĺ—Ä–Ĺ–ł–ļ–Ķ "–†–į–∑–≤–ł—ā–ł–Ķ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł" (1964–≥.), –ĺ—ā–ľ–Ķ—á–į–Ķ—ā, —á—ā–ĺ –≤ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł–Ķ –≥–ĺ–ī—č –Ņ–ĺ—Ź–≤–ł–Ľ–ł—Ā—Ć –≤–ĺ–∑—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ņ—Ä–ĺ—ā–ł–≤ –ĺ–ī–Ĺ–ĺ–≥–ĺ –ł–∑ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č—Ö –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–≤ –®–ł–Ľ–Ľ–Ķ—Ä–į, –≥–Ľ–į—Ā—Ź—Č–Ķ–≥–ĺ, —á—ā–ĺ –≤ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–ľ –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ĺ–ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–Ķ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —ā–Ķ–Ľ–į, —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É–Ķ–ľ–ĺ–≥–ĺ —Ā –Ņ–ĺ–ľ–ĺ—Č—Ć—é –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –ī—Ä—É–≥ –ĺ—ā –ī—Ä—É–≥–į –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤, –Ľ—é–Ī–ĺ–Ļ –ł–∑ —É–Ņ–ĺ–ľ—Ź–Ĺ—É—ā—č—Ö –Ņ–į—Ä–į–ľ–Ķ—Ä–ĺ–≤ –≤–ĺ–∑–≤—Ä–į—Č–į–Ķ—ā—Ā—Ź –ļ —Ā–≤–ĺ–Ķ–ľ—É –Ņ–Ķ—Ä–≤–ĺ–Ĺ–į—á–į–Ľ—Ć–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—é, –ļ–ĺ–≥–ī–į  –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ –≤–ĺ–∑–≤—Ä–į—Č–į–Ķ—ā—Ā—Ź –ļ —Ā–≤–ĺ–ł–ľ. –Ē–į–Ľ–Ķ–Ķ, –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–į–Ķ—ā –§—Ä–į–Ĺ–ļ—Ą—É—Ä—ā, —Ā—Ā—č–Ľ–į—Ź—Ā—Ć –Ĺ–į –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź, "–≤ —ā–į–ļ–ĺ–Ļ –ĺ–Ī—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–Ķ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –Ě. –Ě. –®–ł–Ľ–Ľ–Ķ—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–ł–∑–Ĺ–į–Ĺ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤—č–ľ... –ē—Ā–Ľ–ł –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā—Ć –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –®–ł–Ľ–Ľ–Ķ—Ä–į —É–ļ–į–∑–į–Ĺ–ł–Ķ–ľ, —á—ā–ĺ –≤—Ā–Ķ —á–į—Ā—ā–ł –ł–∑–ľ–Ķ–Ĺ—Ź—é—Č–Ķ–≥–ĺ—Ā—Ź —ā–Ķ–Ľ–į (–ł–Ľ–ł —Ā–ł—Ā—ā–Ķ–ľ—č) –Ĺ–į—Ö–ĺ–ī—Ź—ā—Ā—Ź –≤ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–ľ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł–ł, —ā–ĺ —ć—ā–ĺ—ā –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ –ļ–į–ļ —á–į—Ā—ā–Ĺ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł—Ź —ā–Ķ–Ľ..." [33], [34].
–ě—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É –®–ł–Ľ–Ľ–Ķ—Ä–į ‚ĒÄ –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –ĺ—ā–ľ–Ķ—á–į–Ķ—ā, —á—ā–ĺ –≤ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź—Ö –Ņ–ĺ —ć—ā–ĺ–ľ—É –ľ–Ķ—ā–ĺ–ī—É —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ –ĺ–Ī—Ź–∑–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ĺ–Ī —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł—Ö –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ĺ–≤
–Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ĺ–≤ –≤–ĺ–∑–≤—Ä–į—Č–į–Ķ—ā—Ā—Ź –ļ —Ā–≤–ĺ–ł–ľ. –Ē–į–Ľ–Ķ–Ķ, –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–į–Ķ—ā –§—Ä–į–Ĺ–ļ—Ą—É—Ä—ā, —Ā—Ā—č–Ľ–į—Ź—Ā—Ć –Ĺ–į –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź, "–≤ —ā–į–ļ–ĺ–Ļ –ĺ–Ī—Č–Ķ–Ļ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–Ķ –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –Ě. –Ě. –®–ł–Ľ–Ľ–Ķ—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–ł–∑–Ĺ–į–Ĺ —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤—č–ľ... –ē—Ā–Ľ–ł –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā—Ć –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –®–ł–Ľ–Ľ–Ķ—Ä–į —É–ļ–į–∑–į–Ĺ–ł–Ķ–ľ, —á—ā–ĺ –≤—Ā–Ķ —á–į—Ā—ā–ł –ł–∑–ľ–Ķ–Ĺ—Ź—é—Č–Ķ–≥–ĺ—Ā—Ź —ā–Ķ–Ľ–į (–ł–Ľ–ł —Ā–ł—Ā—ā–Ķ–ľ—č) –Ĺ–į—Ö–ĺ–ī—Ź—ā—Ā—Ź –≤ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–ľ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł–ł, —ā–ĺ —ć—ā–ĺ—ā –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ –ļ–į–ļ —á–į—Ā—ā–Ĺ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł—Ź —ā–Ķ–Ľ..." [33], [34].
–ě—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ņ–ĺ –ľ–Ķ—ā–ĺ–ī—É –®–ł–Ľ–Ľ–Ķ—Ä–į ‚ĒÄ –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –ĺ—ā–ľ–Ķ—á–į–Ķ—ā, —á—ā–ĺ –≤ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź—Ö –Ņ–ĺ —ć—ā–ĺ–ľ—É –ľ–Ķ—ā–ĺ–ī—É —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ –ĺ–Ī—Ź–∑–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ĺ–Ī —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł—Ö –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ĺ–≤  –ĺ–ī–Ĺ–į–ļ–ĺ, –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł—Ź —ć—ā–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č "–ī–ĺ–Ľ–∂–Ĺ–į –Ī—č—ā—Ć –Ņ—Ä–ł–∑–Ĺ–į–Ĺ–į –ĺ—á–Ķ–Ĺ—Ć —Ā—ā–Ķ—Ā–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, —ā–į–ļ –ļ–į–ļ –ĺ–Ī—Č–į—Ź —ā–Ķ–ĺ—Ä–ł—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ĺ–≤ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ–ĺ–≥–ĺ —ā–ł–Ņ–į (—Ą–ĺ—Ä–ľ –ü—Ą–į—Ą—Ą–į) –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–Ķ —ā—Ä—É–ī–Ĺ–ĺ—Ā—ā–ł –ł –ł–∑–Ľ–į–≥–į–Ķ—ā—Ā—Ź –Ľ–ł—ą—Ć –≤ —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö —ā—Ä—É–ī–į—Ö –Ņ–ĺ –≤—č—Ā—ą–Ķ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ." –í –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–Ķ –ļ—É—Ä—Ā–ĺ–≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ī–į—Ď—ā—Ā—Ź –Ī–Ķ–∑ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į, –Ľ–ł–Ī–ĺ –Ņ—Ä–ł–≤–ĺ–ī–ł—ā—Ā—Ź –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ –≤ –Ĺ–Ķ—Ā—ā—Ä–ĺ–≥–ĺ–ľ, —É–Ņ—Ä–ĺ—Č—Ď–Ĺ–Ĺ–ĺ–ľ –≤–ł–ī–Ķ[35].
–ź–Ĺ–į–Ľ–ł–∑–ł—Ä—É—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ –Ņ–ĺ —Ā—Ö–Ķ–ľ–Ķ –ö. –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –ĺ–Ī—Ä–į—Č–į–Ķ—ā –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ –Ĺ–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–ł –Ĺ–Ķ–ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ņ—É—Č–Ķ–Ĺ–ł—Ź –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –≤–ļ–Ľ—é—á–Ķ–Ĺ–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č
–ĺ–ī–Ĺ–į–ļ–ĺ, –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ—Ā—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł—Ź —ć—ā–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č "–ī–ĺ–Ľ–∂–Ĺ–į –Ī—č—ā—Ć –Ņ—Ä–ł–∑–Ĺ–į–Ĺ–į –ĺ—á–Ķ–Ĺ—Ć —Ā—ā–Ķ—Ā–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, —ā–į–ļ –ļ–į–ļ –ĺ–Ī—Č–į—Ź —ā–Ķ–ĺ—Ä–ł—Ź –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ĺ–≤ —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ–ĺ–≥–ĺ —ā–ł–Ņ–į (—Ą–ĺ—Ä–ľ –ü—Ą–į—Ą—Ą–į) –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā –ł–∑–≤–Ķ—Ā—ā–Ĺ—č–Ķ —ā—Ä—É–ī–Ĺ–ĺ—Ā—ā–ł –ł –ł–∑–Ľ–į–≥–į–Ķ—ā—Ā—Ź –Ľ–ł—ą—Ć –≤ —Ā–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö —ā—Ä—É–ī–į—Ö –Ņ–ĺ –≤—č—Ā—ą–Ķ–Ļ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–Ķ." –í –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–Ķ –ļ—É—Ä—Ā–ĺ–≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ī–į—Ď—ā—Ā—Ź –Ī–Ķ–∑ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–į, –Ľ–ł–Ī–ĺ –Ņ—Ä–ł–≤–ĺ–ī–ł—ā—Ā—Ź –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ –≤ –Ĺ–Ķ—Ā—ā—Ä–ĺ–≥–ĺ–ľ, —É–Ņ—Ä–ĺ—Č—Ď–Ĺ–Ĺ–ĺ–ľ –≤–ł–ī–Ķ[35].
–ź–Ĺ–į–Ľ–ł–∑–ł—Ä—É—Ź –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ –Ņ–ĺ —Ā—Ö–Ķ–ľ–Ķ –ö. –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –ĺ–Ī—Ä–į—Č–į–Ķ—ā –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ –Ĺ–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ–ł–ł –Ĺ–Ķ–ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–Ĺ–ĺ–≥–ĺ –ī–ĺ–Ņ—É—Č–Ķ–Ĺ–ł—Ź –ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ –≤–ļ–Ľ—é—á–Ķ–Ĺ–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č  –ł
–ł  ‚ĒÄ —Ą—É–Ĺ–ļ—Ü–ł–ł –≤ —Ā–ĺ—Ā—ā–į–≤ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –ł –Ņ—Ä–ł—Ö–ĺ–ī–ł—ā –ļ –≤—č–≤–ĺ–ī—É, —á—ā–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ķ–Ĺ –≥—Ä—É–Ņ–Ņ–Ķ –ĺ–Ī—Č–ł—Ö —É—Ā–Ľ–ĺ–≤–ł–Ļ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł—Ö –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ĺ–≤
‚ĒÄ —Ą—É–Ĺ–ļ—Ü–ł–ł –≤ —Ā–ĺ—Ā—ā–į–≤ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –Ņ–Ķ—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –ł –Ņ—Ä–ł—Ö–ĺ–ī–ł—ā –ļ –≤—č–≤–ĺ–ī—É, —á—ā–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ķ–Ĺ –≥—Ä—É–Ņ–Ņ–Ķ –ĺ–Ī—Č–ł—Ö —É—Ā–Ľ–ĺ–≤–ł–Ļ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–ł—Ö –ī–Ķ–Ľ–ł—ā–Ķ–Ľ–Ķ–Ļ –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ–ĺ–≤  , –Ĺ–ĺ –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ĺ—á–Ķ–Ĺ –ī–Ľ—Ź —É—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ł—Ź —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –Ņ–Ķ—Ä–≤–ł—á–Ĺ–ĺ–≥–ĺ –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–Ķ–≥–ĺ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ź
, –Ĺ–ĺ –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā–ĺ—á–Ķ–Ĺ –ī–Ľ—Ź —É—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ–ł—Ź —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –Ņ–Ķ—Ä–≤–ł—á–Ĺ–ĺ–≥–ĺ –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–Ķ–≥–ĺ –ī–Ķ–Ľ–ł—ā–Ķ–Ľ—Ź  , —ā–ĺ –Ķ—Ā—ā—Ć –ī–Ľ—Ź –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –Ē–į–Ľ–Ķ–Ķ –ĺ–Ĺ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā, —á—ā–ĺ –Ņ—Ä–ł –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ī–ĺ–Ľ–∂–Ķ–Ĺ –Ī—č—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ —ā–į–ļ–ĺ–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ī—č–Ľ –Ī—č —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ķ–Ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ –Ĺ–Ķ—Ā–ĺ–≤–ľ–Ķ—Ā—ā–ł–ľ–ĺ—Ā—ā–ł –į–ī–ł–į–Ī–į—ā—č –ł –ł–∑–ĺ—ā–Ķ—Ä–ľ—č. –í —ć—ā–ł—Ö –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–łp–ĺ–≤–į–Ĺ–Ĺ—č—Ö –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź—Ö —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ –ł–∑–Ľ–ł—ą–Ĺ–ł–ľ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, —ā–į–ļ –ļ–į–ļ –ĺ–Ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā–Ĺ—č–ľ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ–ľ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ĺ –Ĺ–Ķ—Ā–ĺ–≤–ľ–Ķ—Ā—ā–ł–ľ–ĺ—Ā—ā–ł –į–ī–ł–į–Ī–į—ā—č –ł –ł–∑–ĺ—ā–Ķ—Ä–ľ—č.¬Ľ[36].
, —ā–ĺ –Ķ—Ā—ā—Ć –ī–Ľ—Ź –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. –Ē–į–Ľ–Ķ–Ķ –ĺ–Ĺ —É—ā–≤–Ķ—Ä–∂–ī–į–Ķ—ā, —á—ā–ĺ –Ņ—Ä–ł –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–Ķ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł –ī–ĺ–Ľ–∂–Ķ–Ĺ –Ī—č—ā—Ć –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į–Ĺ —ā–į–ļ–ĺ–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ī—č–Ľ –Ī—č —ć–ļ–≤–ł–≤–į–Ľ–Ķ–Ĺ—ā–Ķ–Ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–Ķ –ĺ –Ĺ–Ķ—Ā–ĺ–≤–ľ–Ķ—Ā—ā–ł–ľ–ĺ—Ā—ā–ł –į–ī–ł–į–Ī–į—ā—č –ł –ł–∑–ĺ—ā–Ķ—Ä–ľ—č. –í —ć—ā–ł—Ö –ļ–ĺ—Ä—Ä–Ķ–ļ—ā–łp–ĺ–≤–į–Ĺ–Ĺ—č—Ö –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź—Ö —Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ –ł–∑–Ľ–ł—ą–Ĺ–ł–ľ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł, —ā–į–ļ –ļ–į–ļ –ĺ–Ĺ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā–Ĺ—č–ľ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ–ľ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ–Ļ —ā–Ķ–ĺ—Ä–Ķ–ľ—č –ĺ –Ĺ–Ķ—Ā–ĺ–≤–ľ–Ķ—Ā—ā–ł–ľ–ĺ—Ā—ā–ł –į–ī–ł–į–Ī–į—ā—č –ł –ł–∑–ĺ—ā–Ķ—Ä–ľ—č.¬Ľ[36].
–ú–Ķ—ā–ĺ–ī –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź
–ü–ĺ —ć—ā–ĺ–ľ—É –ľ–Ķ—ā–ĺ–ī—É –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł —Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ–ĺ –Ĺ–į –ī–≤–į –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į (–Ĺ–į—á–į–Ľ–į):
1. –ü—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł (–í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł).
2. –ü—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł (–í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł).
–ö–į–∂–ī—č–Ļ –ł–∑ —ć—ā–ł—Ö –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–≤ –Ņ–ĺ–Ľ—É—á–ł–Ľ —Ā–į–ľ–ĺ—Ā—ā–ĺ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ –Ĺ–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ—č—Ö –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–≤.
–ü–ĺ—Ā—ā—É–Ľ–į—ā –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł (–Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź):
–Ę–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ķ—Ā—ā—Ć –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—Č–į—Ź –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–Ķ —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į, —ā–ĺ –Ķ—Ā—ā—Ć –ľ–Ķ–∂–ī—É —ā–Ķ–Ľ–į–ľ–ł –ł —ć–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į–ľ–ł —ā–Ķ–Ľ, –Ĺ–Ķ –Ĺ–į—Ö–ĺ–ī—Ź—Č–ł–ľ–ł—Ā—Ź –≤ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–ľ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł–ł, –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ķ–Ĺ –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–Ļ —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ—č–Ļ (–Ņ–ĺ –Ī–į–Ľ–į–Ĺ—Ā—É) –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī —ā–Ķ–Ņ–Ľ–į –≤ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ—č—Ö –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź—Ö ‚ÄĒ –ĺ—ā —ā–Ķ–Ľ –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā—č—Ö –ļ —ā–Ķ–Ľ–į–ľ –ľ–Ķ–Ĺ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā—č–ľ –ł –ĺ–Ī—Ä–į—ā–Ĺ–ĺ[37].
–ü–ĺ—Ā—ā—É–Ľ–į—ā –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź —Ā–į–ľ–ĺ–ĺ—á–Ķ–≤–ł–ī–Ķ–Ĺ, —ā–į–ļ –ļ–į–ļ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —á–į—Ā—ā–Ĺ—č–ľ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ–ľ –Ņ—Ä–ł—á–ł–Ĺ–Ĺ–ĺ–Ļ —Ā–≤—Ź–∑–ł –ł –ĺ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ—Ā—ā–ł –∑–į–ļ–ĺ–Ĺ–ĺ–≤ –Ņ—Ä–ł—Ä–ĺ–ī—č. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –Ķ—Ā–Ľ–ł —Ā—É—Č–Ķ—Ā—ā–≤—É–Ķ—ā –Ņ—Ä–ł—á–ł–Ĺ–į, –≤ —Ā–ł–Ľ—É –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ –≤ –ī–į–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ —ā–Ķ–Ņ–Ľ–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –ľ–Ķ–Ĺ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–ľ—É, —ā–ĺ —ć—ā–į –Ņ—Ä–ł—á–ł–Ĺ–į –≤ —ā–Ķ—Ö –∂–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö –Ī—É–ī–Ķ—ā –Ņ—Ä–Ķ–Ņ—Ź—ā—Ā—ā–≤–ĺ–≤–į—ā—Ć –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī—É —ā–Ķ–Ņ–Ľ–į –≤ –Ņ—Ä–ĺ—ā–ł–≤–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł, –ł –Ĺ–į–ĺ–Ī–ĺ—Ä–ĺ—ā. –≠—ā–ĺ—ā –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ķ–Ĺ –≤ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–ł –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, —ā–į–ļ –ļ–į–ļ –Ĺ–Ķ —Ā–ĺ–ī–Ķ—Ä–∂–ł—ā –Ĺ–ł–ļ–į–ļ–ł—Ö —É–ļ–į–∑–į–Ĺ–ł–Ļ –ĺ –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ –≤ –ľ–ł—Ä–Ķ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä.
–°–Ľ–Ķ–ī—Ā—ā–≤–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł:
–°–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ I. –Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ķ (–≤ —Ä–į–ľ–ļ–į—Ö –ĺ–ī–Ĺ–ĺ–Ļ –ł —ā–ĺ–Ļ –∂–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ- –≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ł–Ľ–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä) –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ľ–Ĺ—č—Ö –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ —ā–Ķ–Ņ–Ľ–į –≤ —Ä–į–Ī–ĺ—ā—É –ł —Ä–į–Ī–ĺ—ā—č –≤ —ā–Ķ–Ņ–Ľ–ĺ.
–°–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ II. (—ā–Ķ–ĺ—Ä–Ķ–ľ–į –Ĺ–Ķ—Ā–ĺ–≤–ľ–Ķ—Ā—ā–ł–ľ–ĺ—Ā—ā–ł –į–ī–ł–į–Ī–į—ā—č –ł –ł–∑–ĺ—ā–Ķ—Ä–ľ—č). –Ě–į –ł–∑–ĺ—ā–Ķ—Ä–ľ–Ķ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—Č–Ķ–Ļ –ī–≤–Ķ —Ä–į–∑–Ľ–ł—á–Ĺ—č–Ķ –į–ī–ł–į–Ī–į—ā—č —ā–ĺ–Ļ –∂–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č, —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ä–į–≤–Ķ–Ĺ –Ĺ—É–Ľ—é.
–°–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ III (—ā–Ķ–ĺ—Ä–Ķ–ľ–į —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–ł—Ź —ā–Ķ–Ľ). –í —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č—Ö –ļ—Ä—É–≥–ĺ–≤—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į—Ö –ī–≤—É—Ö —ā–Ķ—Ä–ľ–ł—á–Ķ—Ā–ļ–ł —Ā–ĺ–Ņ—Ä—Ź–∂—Ď–Ĺ–Ĺ—č—Ö —ā–Ķ–Ľ  , –ĺ–Ī—Ä–į–∑—É—é—Č–ł—Ö –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—É—é —Ā–ł—Ā—ā–Ķ–ľ—É, –ĺ–Ī–į —ā–Ķ–Ľ–į –≤–ĺ–∑–≤—Ä–į—Č–į—é—ā—Ā—Ź –Ĺ–į –ł—Ā—Ö–ĺ–ī–Ĺ—č–Ķ –į–ī–ł–į–Ī–į—ā—č –ł –≤ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ. [38].
, –ĺ–Ī—Ä–į–∑—É—é—Č–ł—Ö –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—É—é —Ā–ł—Ā—ā–Ķ–ľ—É, –ĺ–Ī–į —ā–Ķ–Ľ–į –≤–ĺ–∑–≤—Ä–į—Č–į—é—ā—Ā—Ź –Ĺ–į –ł—Ā—Ö–ĺ–ī–Ĺ—č–Ķ –į–ī–ł–į–Ī–į—ā—č –ł –≤ –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ĺ–ī–Ĺ–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ. [38].
–Ě–į –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ —Ā—Ö–Ķ–ľ—č –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ī–Ľ—Ź –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –ł –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤  [39].
[39].
–ü–ĺ—Ā—ā—É–Ľ–į—ā –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł:
–†–į–Ī–ĺ—ā–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ł –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–į –≤ —ā–Ķ–Ņ–Ľ–ĺ –Ņ—É—ā—Ď–ľ —ā—Ä–Ķ–Ĺ–ł—Ź –ł–Ľ–ł —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–į–≥—Ä–Ķ–≤–į.
–°–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ I.–Ę–Ķ–Ņ–Ľ–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ņ—Ä–Ķ–≤—Ä–į—Č–Ķ–Ĺ–ĺ –≤ —Ä–į–Ī–ĺ—ā—É (–Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –ł—Ā–ļ–Ľ—é—á—Ď–Ĺ–Ĺ–ĺ–≥–ĺ Perpetuum mobile II —Ä–ĺ–ī–į):
 .
.
–°–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ II. –ö–ü–Ē –ł–Ľ–ł —Ö–ĺ–Ľ–ĺ–ī–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā—Ć –Ľ—é–Ī–ĺ–Ļ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ–Ļ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ –ľ–į—ą–ł–Ĺ—č –Ņ—Ä–ł –∑–į–ī–į–Ĺ–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į—Ö –≤–Ĺ–Ķ—ą–Ĺ–ł—Ö –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–≤ –≤—Ā–Ķ–≥–ī–į –ľ–Ķ–Ĺ—Ć—ą–Ķ –ö–ü–Ē –ł–Ľ–ł —Ö–ĺ–Ľ–ĺ–ī–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –ľ–į—ą–ł–Ĺ, —Ä–į–Ī–ĺ—ā–į—é—Č–ł—Ö –ľ–Ķ–∂–ī—É —ā–Ķ–ľ–ł –∂–Ķ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į–ľ–ł.
–°–Ĺ–ł–∂–Ķ–Ĺ–ł–Ķ –ö–ü–Ē –ł —Ö–ĺ–Ľ–ĺ–ī–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–Ņ–Ľ–ĺ–≤—č—Ö –ľ–į—ą–ł–Ĺ —Ā–≤—Ź–∑–į–Ĺ–ĺ —Ā –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č–ľ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–ĺ–ľ –ł–∑-–∑–į —Ä–į–∑–Ĺ–ĺ—Ā—ā–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–ĺ–≤ —ā–Ķ–Ņ–Ľ–į –ł —Ä–į–Ī–ĺ—á–Ķ–≥–ĺ —ā–Ķ–Ľ–į –ł –∑–į —Ā—á—Ď—ā –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ—č—Ö –Ņ–ĺ—ā–Ķ—Ä—Ć —Ä–į–Ī–ĺ—ā—č –Ĺ–į —ā—Ä–Ķ–Ĺ–ł–Ķ –ł –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ł–Ķ —Ā–ĺ–Ņ—Ä–ĺ—ā–ł–≤–Ľ–Ķ–Ĺ–ł—Ź. –ė–∑ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł—Ź I –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł –ł —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł—Ź II –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –≤—č—ā–Ķ–ļ–į–Ķ—ā –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–Ľ–Ķ–Ĺ–ł—Ź Perpetuum mobile I –ł II —Ä–ĺ–ī–į.
–ď–ĺ–≤–ĺ—Ä—Ź –ĺ —Ā—ā–Ķ–Ņ–Ķ–Ĺ–ł –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā–ł –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–ĺ–≤ –ł —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É—é—Č–ł—Ö –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –ĺ—ā–ľ–Ķ—á–į–Ķ—ā, —á—ā–ĺ –Ņ–Ķ—Ä–≤—č–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā - –∑–į–ļ–ĺ–Ĺ —Ā–ĺ—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł—Ź —ć–Ĺ–Ķ—Ä–≥–ł–ł ‚ÄĒ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –Ņ–Ķ—Ä–≤–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ–Ķ–Ĺ –≤ —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö –Ľ—é–Ī—č—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, –Ņ—Ä–ĺ—ā–Ķ–ļ–į—é—Č–ł—Ö –≤ –Ņ—Ä–ł—Ä–ĺ–ī–Ķ; –≤—ā–ĺ—Ä–ĺ–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā ( –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź) —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł ‚ÄĒ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ–ľ –ļ–į–ļ —á–į—Ā—ā–Ĺ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –Ņ—Ä–ł—á–ł–Ĺ–Ĺ–ĺ–Ļ —Ā–≤—Ź–∑–ł —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ –Ņ—Ä–ł—Ä–ĺ–ī—č, –Ĺ–ĺ –Ķ–≥–ĺ —É—Ä–ĺ–≤–Ķ–Ĺ—Ć –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā–ł —Ā–Ĺ–ł–∂–į–Ķ—ā—Ā—Ź –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ —É–ļ–į–∑–į–Ĺ–ł–Ķ–ľ –≤–∑–į–ł–ľ–ĺ—Ā–≤—Ź–∑–ł –Ņ–ĺ–Ĺ—Ź—ā–ł–Ļ ¬ę—ā–Ķ–Ņ–Ľ–嬼 –ł ¬ę—ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į¬Ľ; —ā—Ä–Ķ—ā–ł–Ļ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā ‚ÄĒ –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł (–Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł) –ł–ľ–Ķ–Ķ—ā —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ł–Ļ —Ö–į—Ä–į–ļ—ā–Ķ—Ä –ł —Ä–į—Ā—Ā–ľ–į—ā—Ä–ł–≤–į–Ķ—ā—Ā—Ź –ļ–į–ļ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ–ľ –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł–ł —ā–Ķ—á–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –Ĺ–į–Ī–Ľ—é–ī–į–Ķ–ľ—č—Ö —Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ –Ņ—Ä–ł—Ä–ĺ–ī—č. [40].
–í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ī–Ľ—Ź —Ā–ł—Ā—ā–Ķ–ľ —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł
–Ě–į –Ņ–Ķ—Ä–≤—č–Ļ –≤–∑–≥–Ľ—Ź–ī —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —Ā–ł—Ā—ā–Ķ–ľ–į —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł –≤—č–≥–Ľ—Ź–ī–ł—ā –į–Ī—Ā—É—Ä–ī–Ĺ—č–ľ, —ā–į–ļ –ļ–į–ļ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł—ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č, –Ņ—Ä–ł–Ĺ—Ź—ā–ĺ–ľ—É –≤ –ĺ–Ī—Č–ł—Ö –ļ—É—Ä—Ā–į—Ö —Ą–ł–∑–ł–ļ–ł –ł –≤ –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ (—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–Ļ) —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ. –Ē–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ, —Ā–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –≤—ā–ĺ—Ä–ĺ–ľ—É –Ĺ–į—á–į–Ľ—É —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä  ,
, –ī–≤—É—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –≤—č—Ä–į–∂–į–Ķ—ā—Ā—Ź –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ
–ī–≤—É—Ö —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ—č –≤—č—Ä–į–∂–į–Ķ—ā—Ā—Ź –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–Ķ–Ļ

–ě—ā—Ā—é–ī–į —Ź–ļ–ĺ–Ī—č –ī–Ķ–Ľ–į–Ľ—Ā—Ź –≤—č–≤–ĺ–ī, —á—ā–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –ľ–Ķ–Ĺ—Ź—ā—Ć –∑–Ĺ–į–ļ: –ĺ–Ĺ–į –ī–ĺ–Ľ–∂–Ĺ–į –Ī—č—ā—Ć –≤—Ā–Ķ–≥–ī–į –Ľ–ł–Ī–ĺ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, –Ľ–ł–Ī–ĺ –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ. –Ě–į —Ā–į–ľ–ĺ–ľ –ī–Ķ–Ľ–Ķ –≤—Ā—Ď —ć—ā–ĺ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā—Ā—Ź –ļ –ļ–≤–į–∑–ł—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ł–ľ (—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č–ľ) –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–į–ľ –ł–∑ –ĺ–ī–Ĺ–ĺ–≥–ĺ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –≤ –ī—Ä—É–≥–ĺ–Ķ –ī–Ľ—Ź –ĺ–Ī—č—á–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ, —ā–ĺ –Ķ—Ā—ā—Ć —Ā–ł—Ā—ā–Ķ–ľ —Ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł (–Ņ–ĺ —Ā–ĺ–≥–Ľ–į—ą–Ķ–Ĺ–ł—é) –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł, –Ĺ–ĺ –Ĺ–Ķ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā—Ā—Ź –ļ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–į–ľ –ł–∑ –ĺ–ī–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –≤ –ī—Ä—É–≥–ĺ–Ķ –Ĺ–Ķ—Ā—ā–į—ā–ł—á–Ķ—Ā–ļ–ł–ľ –Ņ—É—ā—Ď–ľ. –í—č–≤–ĺ–ī –ĺ —ā–ĺ–ľ, —á—ā–ĺ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –ľ–Ķ–Ĺ—Ź—ā—Ć –∑–Ĺ–į–ļ, –Ĺ–Ķ –≤—č—ā–Ķ–ļ–į–Ķ—ā –ł–∑ –≤—č—ą–Ķ–Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ī–Ķ–∑ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑–į–Ņ—Ä–Ķ—ā–į –Ĺ–į –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –Ĺ–į—Ä—Ź–ī—É —Ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł ‚ÄĒ –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä. –Ę–į–ļ–ĺ–Ļ –≤—č–≤–ĺ–ī –Ī—É–ī–Ķ—ā —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤—č–ľ, –Ķ—Ā–Ľ–ł –ļ –Ĺ–Ķ–ľ—É –Ņ—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ–ł—ā—Ć –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ķ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ, —á—ā–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–∂–Ĺ–ĺ –ī–ĺ—Ā—ā–ł—á—Ć –ł–∑ –ī–į–Ĺ–Ĺ–ĺ–≥–ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č–ľ –Ņ—É—ā—Ď–ľ, –≤—Ā–Ķ–≥–ī–į –ī–ĺ—Ā—ā–ł–∂–ł–ľ—č –ł–∑ –Ĺ–Ķ–≥–ĺ –ł –Ņ—É—ā—Ď–ľ —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č–ľ. –≠—ā–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –≤–Ķ—Ä–Ĺ–ĺ –ī–Ľ—Ź –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ —á–į—Ā—ā–ĺ –≤—Ā—ā—Ä–Ķ—á–į—é—Č–ł—Ö—Ā—Ź –ĺ–Ī—č—á–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ. –Ē–Ľ—Ź –Ĺ–ł—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ—ā –ł–∑–ľ–Ķ–Ĺ—Ź—ā—Ć —Ā–≤–ĺ–Ļ –∑–Ĺ–į–ļ. –ě–Ĺ–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ľ–ł–Ī–ĺ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, –Ľ–ł–Ī–ĺ –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ. –í–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –Ĺ–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł—ā —ā–į–ļ–∂–Ķ —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł—é –ł–∑ —ā—Ä–Ķ—ā—Ć–Ķ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ĺ –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ–ĺ—Ā—ā–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–≥–ĺ –Ĺ—É–Ľ—Ź ( ). –≠—ā–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –∑–į–Ņ—Ä–Ķ—Č–į–Ķ—ā –Ľ–ł—ą—Ć –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī —á–Ķ—Ä–Ķ–∑ –Ĺ–Ķ–≥–ĺ –ł–∑ –ĺ–Ī–Ľ–į—Ā—ā–ł –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –≤ –ĺ–Ī–Ľ–į—Ā—ā—Ć —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö. [41]
). –≠—ā–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –∑–į–Ņ—Ä–Ķ—Č–į–Ķ—ā –Ľ–ł—ą—Ć –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī —á–Ķ—Ä–Ķ–∑ –Ĺ–Ķ–≥–ĺ –ł–∑ –ĺ–Ī–Ľ–į—Ā—ā–ł –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –≤ –ĺ–Ī–Ľ–į—Ā—ā—Ć —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö. [41]
–° –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ-–ļ–ł–Ĺ–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ā–ĺ—á–ļ–ł –∑—Ä–Ķ–Ĺ–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź –ļ–į–ļ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–į—Ź –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—é—Č–į—Ź –ł–Ĺ—ā–Ķ–Ĺ—Ā–ł–≤–Ĺ–ĺ—Ā—ā—Ć —Ö–į–ĺ—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ (—ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–≥–ĺ) –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź –≤—Ā–Ķ–Ļ —Ā–ĺ–≤–ĺ–ļ—É–Ņ–Ĺ–ĺ—Ā—ā–ł —á–į—Ā—ā–ł—Ü —Ā–ł—Ā—ā–Ķ–ľ—č, –ł –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ĺ–Ĺ–į–Ľ—Ć–Ĺ–į—Ź —Ā—Ä–Ķ–ī–Ĺ–Ķ–Ļ –ļ–ł–Ĺ–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —ć–Ĺ–Ķ—Ä–≥–ł–ł –Ņ–ĺ—Ā—ā—É–Ņ–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ–Ļ —á–į—Ā—ā–ł—Ü—č. –°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —Ā–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—é –ú–į–ļ—Ā–≤–Ķ–Ľ–Ľ–į —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ķ—ā—Ā—Ź —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ–ľ
 _v
_v
–ė–∑ —ć—ā–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –Ņ–ĺ –ľ–Ķ—Ä–Ķ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –Ņ—Ä–ł –Ņ–ĺ–ī–≤–ĺ–ī–Ķ —ć–Ĺ–Ķ—Ä–≥–ł–ł, –≤—Ā–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ —á–į—Ā—ā–ł—Ü –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –Ĺ–į –≤–Ķ—Ä—Ö–Ĺ–ł–Ķ —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —É—Ä–ĺ–≤–Ĺ–ł –ł, —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, —É—Ā–ł–Ľ–ł–≤–į–Ķ—ā—Ā—Ź –Ī–Ķ—Ā–Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —Ā–ł—Ā—ā–Ķ–ľ—č, —ā–į–ļ –ļ–į–ļ —á–į—Ā—ā–ł—Ü—č –ļ–į–∂–ī—č–Ļ —Ä–į–∑ —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—ā—Ā—Ź –Ņ–ĺ –Ī–ĺŐĀ–Ľ—Ć—ą–Ķ–ľ—É —á–ł—Ā–Ľ—É —É—Ä–ĺ–≤–Ĺ–Ķ–Ļ. –ü—Ä–ł —Ä–ĺ—Ā—ā–Ķ —ć–Ĺ–Ķ—Ä–≥–ł–ł –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É  –ł
–ł  –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č, —ā–ĺ –ł –ł—Ö –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ —ā–į–ļ–∂–Ķ –Ī—É–ī–Ķ—ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ. –ė–∑ —Ą–ĺ—Ä–ľ—É–Ľ—č –ú–į–ļ—Ā–≤–Ķ–Ľ–Ľ–į —ā–į–ļ–∂–Ķ —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –ī–Ľ—Ź —ā–ĺ–≥–ĺ —á—ā–ĺ–Ī—č –Ņ—Ä–ł —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–ł —ć–Ĺ–Ķ—Ä–≥–ł–ł —Ā–ł—Ā—ā–Ķ–ľ—č —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ī—č–Ľ–į –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ , —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā–ł—Ā—ā–Ķ–ľ—č.
–Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č, —ā–ĺ –ł –ł—Ö –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ —ā–į–ļ–∂–Ķ –Ī—É–ī–Ķ—ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ. –ė–∑ —Ą–ĺ—Ä–ľ—É–Ľ—č –ú–į–ļ—Ā–≤–Ķ–Ľ–Ľ–į —ā–į–ļ–∂–Ķ —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –ī–Ľ—Ź —ā–ĺ–≥–ĺ —á—ā–ĺ–Ī—č –Ņ—Ä–ł —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–ł —ć–Ĺ–Ķ—Ä–≥–ł–ł —Ā–ł—Ā—ā–Ķ–ľ—č —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ī—č–Ľ–į –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ , —ā—Ä–Ķ–Ī—É–Ķ—ā—Ā—Ź —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā–ł—Ā—ā–Ķ–ľ—č.
–ö—Ä–ĺ–ľ–Ķ –ľ–ĺ–Ľ–Ķ–ļ—É–Ľ—Ź—Ä–Ĺ–ĺ-–ļ–ł–Ĺ–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ļ–į–ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ—č, —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł–∑—É—é—Č–Ķ–Ļ –ł–Ĺ—ā–Ķ–Ĺ—Ā–ł–≤–Ĺ–ĺ—Ā—ā—Ć –ī–≤–ł–∂–Ķ–Ĺ–ł—Ź —á–į—Ā—ā–ł—Ü, —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ķ—Ā—ā—Ć –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—é—Č–į—Ź —Ä–į—Ā–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ —á–į—Ā—ā–ł—Ü –Ņ–ĺ —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–ľ —É—Ä–ĺ–≤–Ĺ—Ź–ľ (—Ą–ĺ—Ä–ľ—É–Ľ–į –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į):
 ,
,
–≥–ī–Ķ  —Ė
—Ė  ‚ÄĒ —á–ł—Ā–Ľ–ĺ —á–į—Ā—ā–ł—Ü –Ĺ–į –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–ľ —É—Ä–ĺ–≤–Ĺ–Ķ –ł –Ĺ–į —É—Ä–ĺ–≤–Ķ
‚ÄĒ —á–ł—Ā–Ľ–ĺ —á–į—Ā—ā–ł—Ü –Ĺ–į –ł—Ā—Ö–ĺ–ī–Ĺ–ĺ–ľ —É—Ä–ĺ–≤–Ĺ–Ķ –ł –Ĺ–į —É—Ä–ĺ–≤–Ķ  .
.
–ü—Ä–ł —Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ–ĺ–ľ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–ł —Ā–ł—Ā—ā–Ķ–ľ—č –ł –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č 
 –≤—Ā–Ķ–≥–ī–į –ľ–Ķ–Ĺ—Ć—ą–Ķ,—á–Ķ–ľ
–≤—Ā–Ķ–≥–ī–į –ľ–Ķ–Ĺ—Ć—ą–Ķ,—á–Ķ–ľ  . –Ě–ĺ, –Ķ—Ā–Ľ–ł —Ä–Ķ–į–Ľ–ł–∑–ĺ–≤–į—ā—Ć —Ā–ł—Ā—ā–Ķ–ľ—É, –≥–ī–Ķ
. –Ě–ĺ, –Ķ—Ā–Ľ–ł —Ä–Ķ–į–Ľ–ł–∑–ĺ–≤–į—ā—Ć —Ā–ł—Ā—ā–Ķ–ľ—É, –≥–ī–Ķ  , —ā–ĺ —ć—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ľ–ĺ –Ī—č, —á—ā–ĺ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć —Ä–Ķ–į–Ľ–ł–∑–ĺ–≤–į–Ĺ—č –Ĺ–Ķ –≤ –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ł—Ö, –į —ā–ĺ–Ľ—Ć–ļ–ĺ –≤ –ļ–≤–į–Ĺ—ā–ĺ–≤—č—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö —Ā –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–ľ —á–ł—Ā–Ľ–ĺ–ľ —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —É—Ä–ĺ–≤–Ĺ–Ķ–Ļ –ł, —Ā —É—á—Ď—ā–ĺ–ľ —ā–ĺ–≥–ĺ, —á—ā–ĺ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –ĺ–∑–Ĺ–į—á–į–Ķ—ā —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć –Ī–Ķ—Ā–Ņ–ĺ—Ä—Ź–ī–ļ–į —Ā–ł—Ā—ā–Ķ–ľ—č. –í —ā–į–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –Ņ—Ä–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–ľ –Ĺ—É–Ľ–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –≤—Ā–Ķ —á–į—Ā—ā–ł—Ü—č –Ī—É–ī—É—ā –∑–į–Ĺ–ł–ľ–į—ā—Ć –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ķ —Ā–į–ľ—č–Ķ –Ĺ–ł–∑–ļ–ł–Ķ —É—Ä–ĺ–≤–Ĺ–ł –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ī—É–ī–Ķ—ā —Ä–į–≤–Ĺ–į –Ĺ—É–Ľ—é. –° —Ä–ĺ—Ā—ā–ĺ–ľ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —á–į—Ā—ā–ł—Ü—č –Ī—É–ī—É—ā –∑–į–Ĺ–ł–ľ–į—ā—Ć –≤—Ā–Ķ –Ī–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ–ł–Ķ —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —É—Ä–ĺ–≤–Ĺ–ł –ł –Ĺ–į—Ā—ā—É–Ņ–ł—ā –ľ–ĺ–ľ–Ķ–Ĺ—ā, –ļ–ĺ–≥–ī–į –≤—Ā–Ķ —É—Ä–ĺ–≤–Ĺ–ł –Ī—É–ī—É—ā –∑–į—Ā–Ķ–Ľ–Ķ–Ĺ—č —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ (
, —ā–ĺ —ć—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ľ–ĺ –Ī—č, —á—ā–ĺ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć —Ä–Ķ–į–Ľ–ł–∑–ĺ–≤–į–Ĺ—č –Ĺ–Ķ –≤ –ļ–Ľ–į—Ā—Ā–ł—á–Ķ—Ā–ļ–ł—Ö, –į —ā–ĺ–Ľ—Ć–ļ–ĺ –≤ –ļ–≤–į–Ĺ—ā–ĺ–≤—č—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö —Ā –ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–ľ —á–ł—Ā–Ľ–ĺ–ľ —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —É—Ä–ĺ–≤–Ĺ–Ķ–Ļ –ł, —Ā —É—á—Ď—ā–ĺ–ľ —ā–ĺ–≥–ĺ, —á—ā–ĺ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –ĺ–∑–Ĺ–į—á–į–Ķ—ā —Ā—ā–Ķ–Ņ–Ķ–Ĺ—Ć –Ī–Ķ—Ā–Ņ–ĺ—Ä—Ź–ī–ļ–į —Ā–ł—Ā—ā–Ķ–ľ—č. –í —ā–į–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –Ņ—Ä–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–ľ –Ĺ—É–Ľ–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –≤—Ā–Ķ —á–į—Ā—ā–ł—Ü—č –Ī—É–ī—É—ā –∑–į–Ĺ–ł–ľ–į—ā—Ć –Ķ–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ķ —Ā–į–ľ—č–Ķ –Ĺ–ł–∑–ļ–ł–Ķ —É—Ä–ĺ–≤–Ĺ–ł –ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ī—É–ī–Ķ—ā —Ä–į–≤–Ĺ–į –Ĺ—É–Ľ—é. –° —Ä–ĺ—Ā—ā–ĺ–ľ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —á–į—Ā—ā–ł—Ü—č –Ī—É–ī—É—ā –∑–į–Ĺ–ł–ľ–į—ā—Ć –≤—Ā–Ķ –Ī–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ–ł–Ķ —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —É—Ä–ĺ–≤–Ĺ–ł –ł –Ĺ–į—Ā—ā—É–Ņ–ł—ā –ľ–ĺ–ľ–Ķ–Ĺ—ā, –ļ–ĺ–≥–ī–į –≤—Ā–Ķ —É—Ä–ĺ–≤–Ĺ–ł –Ī—É–ī—É—ā –∑–į—Ā–Ķ–Ľ–Ķ–Ĺ—č —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ ( , —á—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ļ –Ī–Ķ—Ā–Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —Ā–ł—Ā—ā–Ķ–ľ—č
, —á—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā –Ĺ–į–ł–Ī–ĺ–Ľ–Ķ–Ķ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č–Ļ –Ī–Ķ—Ā–Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —Ā–ł—Ā—ā–Ķ–ľ—č  , –į —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į, –≤ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–ł —Ā —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į, –Ī—É–ī–Ķ—ā
, –į —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į, –≤ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ł–ł —Ā —Ą–ĺ—Ä–ľ—É–Ľ–ĺ–Ļ –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į, –Ī—É–ī–Ķ—ā 
 .
–ē—Ā–Ľ–ł –ī–į–Ľ—Ć—ą–Ķ –Ņ–ĺ–ī–≤–ĺ–ī–ł—ā—Ć —ć–Ĺ–Ķ—Ä–≥–ł—é –≤ —Ā–ł—Ā—ā–Ķ–ľ—É, —ā–ĺ –≤—Ā–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ–Ķ —á–ł—Ā–Ľ–ĺ —á–į—Ā—ā–ł—Ü –Ī—É–ī–Ķ—ā —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ĺ —ā–ĺ–Ľ—Ć–ļ–ĺ –Ĺ–į –≤—č—Ā–ĺ–ļ–ł—Ö —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —É—Ä–ĺ–≤–Ĺ—Ź—Ö –ł, –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā
.
–ē—Ā–Ľ–ł –ī–į–Ľ—Ć—ą–Ķ –Ņ–ĺ–ī–≤–ĺ–ī–ł—ā—Ć —ć–Ĺ–Ķ—Ä–≥–ł—é –≤ —Ā–ł—Ā—ā–Ķ–ľ—É, —ā–ĺ –≤—Ā–Ķ –Ī–ĺ–Ľ—Ć—ą–Ķ–Ķ —á–ł—Ā–Ľ–ĺ —á–į—Ā—ā–ł—Ü –Ī—É–ī–Ķ—ā —Ä–į—Ā–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ĺ —ā–ĺ–Ľ—Ć–ļ–ĺ –Ĺ–į –≤—č—Ā–ĺ–ļ–ł—Ö —ć–Ĺ–Ķ—Ä–≥–Ķ—ā–ł—á–Ķ—Ā–ļ–ł—Ö —É—Ä–ĺ–≤–Ĺ—Ź—Ö –ł, –Ņ–ĺ —Ā—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—é —Ā  , —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź –Ī–ĺŐĀ–Ľ—Ć—ą–į—Ź —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č —É–ľ–Ķ–Ĺ—Ć—ą–ł—ā—Ā—Ź. –°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –≤—č—ą–Ķ–Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č–ľ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ –ú–į–ļ—Ā–≤–Ķ–Ľ–Ľ–į –ł –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į, —ć—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā, —á—ā–ĺ –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ł–ľ–Ķ—é—ā –ľ–Ķ—Ā—ā–ĺ –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č. –ē—Ā–Ľ–ł –≤—Ā–Ķ —á–į—Ā—ā–ł—Ü—č —Ā–ĺ–Ī–Ķ—Ä—É—ā—Ā—Ź –Ĺ–į –≤—č—Ā—ą–Ķ–ľ —É—Ä–ĺ–≤–Ĺ–Ķ, —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ–į—Ź —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć (
, —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź –Ī–ĺŐĀ–Ľ—Ć—ą–į—Ź —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź —Ā–ł—Ā—ā–Ķ–ľ—č —É–ľ–Ķ–Ĺ—Ć—ą–ł—ā—Ā—Ź. –°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –≤—č—ą–Ķ–Ņ—Ä–ł–≤–Ķ–ī—Ď–Ĺ–Ĺ—č–ľ —Ą–ĺ—Ä–ľ—É–Ľ–į–ľ –ú–į–ļ—Ā–≤–Ķ–Ľ–Ľ–į –ł –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ–į, —ć—ā–ĺ –ĺ–∑–Ĺ–į—á–į–Ķ—ā, —á—ā–ĺ –≤ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ł–ľ–Ķ—é—ā –ľ–Ķ—Ā—ā–ĺ –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č. –ē—Ā–Ľ–ł –≤—Ā–Ķ —á–į—Ā—ā–ł—Ü—č —Ā–ĺ–Ī–Ķ—Ä—É—ā—Ā—Ź –Ĺ–į –≤—č—Ā—ą–Ķ–ľ —É—Ä–ĺ–≤–Ĺ–Ķ, —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā—Ā—Ź –Ņ–ĺ–Ľ–Ĺ–į—Ź —É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć ( ). [42].
). [42].
–°–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł –Ĺ–Ķ —ā–ĺ–Ľ—Ć–ļ–ĺ –≤–ĺ–∑–ľ–ĺ–∂–Ĺ—č, –Ĺ–ĺ –ł —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā –≤ –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł. –í 1951 –≥–ĺ–ī—É –Ņ—Ä–ł –ł–∑—É—á–Ķ–Ĺ–ł–ł —Ź–ī–Ķ—Ä–Ĺ—č—Ö —Ā–Ņ–ł–Ĺ–ĺ–≤ –≤ —á–ł—Ā—ā—č—Ö –ļ—Ä–ł—Ā—ā–į–Ľ–Ľ–į—Ö —Ą—ā–ĺ—Ä–ł—Ā—ā–ĺ–≥–ĺ –Ľ–ł—ā–ł—Ź (LiF) –Ī—č–Ľ–ĺ –ĺ–Ī–Ĺ–į—Ä—É–∂–Ķ–Ĺ–ĺ, —á—ā–ĺ –Ņ—Ä–ł —Ā–Ľ–ĺ–∂–Ĺ–ĺ–ľ –≤–ĺ–∑–ī–Ķ–Ļ—Ā—ā–≤–ł–ł —Ā–ł–Ľ—Ć–Ĺ–ĺ–≥–ĺ –ľ–į–≥–Ĺ–ł—ā–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–Ľ—Ź –ł–Ľ–ł –≤—č—Ā–ĺ–ļ–ĺ—á–į—Ā—ā–ĺ—ā–Ĺ–ĺ–≥–ĺ –ł–ľ–Ņ—É–Ľ—Ć—Ā–į, —Ź–ī–Ķ—Ä–Ĺ—č–Ķ —Ā–Ņ–ł–Ĺ—č –ĺ—Ä–ł–Ķ–Ĺ—ā–ł—Ä—É—é—ā—Ā—Ź –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ –Ņ—Ä–ĺ—ā–ł–≤ –Ņ–ĺ–Ľ—Ź, —ā–ĺ –Ķ—Ā—ā—Ć —ā–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –ļ–į–ļ –Ķ—Ā–Ľ–ł –Ī—č –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–į—Ź —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į –Ī—č–Ľ–į –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–ĺ–Ļ. –£—Ā–Ľ–ĺ–≤–ł—Ź, –≤ –ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā—É—Č–Ķ—Ā—ā–≤—É—é—ā —Ā–ł—Ā—ā–Ķ–ľ—č —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł, —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –Ĺ–į—Ā—ā–ĺ–Ľ—Ć–ļ–ĺ –∂—Ď—Ā—ā–ļ–ł–ľ–ł, —á—ā–ĺ –ĺ–Ĺ–ł —Ä–Ķ–ī–ļ–ĺ –≤—Ā—ā—Ä–Ķ—á–į—é—ā—Ā—Ź –Ĺ–į –Ņ—Ä–į–ļ—ā–ł–ļ–Ķ, –Ņ–ĺ–ļ–į —ā–ĺ–Ľ—Ć–ļ–ĺ –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö —Ź–ī–Ķ—Ä–Ĺ—č—Ö —Ā–Ņ–ł–Ĺ–ĺ–≤. –ě—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ī–ĺ—Ā—ā–ł–≥–į—é—ā—Ā—Ź –Ĺ–Ķ –Ņ—É—ā—Ď–ľ –ĺ—ā–Ĺ—Ź—ā–ł—Ź —É —Ā–ł—Ā—ā–Ķ–ľ—č –≤—Ā–Ķ–≥–ĺ —ā–Ķ–Ņ–Ľ–į, –į, –Ĺ–į–ĺ–Ī–ĺ—Ä–ĺ—ā, —Ā–ĺ–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ–ľ —Ā–ł—Ā—ā–Ķ–ľ–Ķ —ć–Ĺ–Ķ—Ä–≥–ł–ł –Ī–ĺ–Ľ—Ć—ą–Ķ —ā–ĺ–Ļ, —á—ā–ĺ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ. –Ě–į –Ņ–Ķ—Ä–≤—č–Ļ –≤–∑–≥–Ľ—Ź–ī —ć—ā–ĺ –≤—č–≥–Ľ—Ź–ī–ł—ā –į–Ī—Ā—É—Ä–ī–ĺ–ľ, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É —É –Ī–ĺ–Ľ—Ć—ą–ł–Ĺ—Ā—ā–≤–į —ā–Ķ–Ľ —Ā —Ä–ĺ—Ā—ā–ĺ–ľ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ī–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł —Ä–į—Ā—ā—Ď—ā –ī–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł –ł –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ—Ź—Ź —ć–Ĺ–Ķ—Ä–≥–ł—Ź. –Ę–į–ļ–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ—č –Ĺ–Ķ –ľ–ĺ–≥—É—ā –Ĺ–į—Ö–ĺ–ī–ł—ā—Ć—Ā—Ź –≤ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—Ö —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł. –Ě–ĺ —É –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č—Ö —Ā–ł—Ā—ā–Ķ–ľ —Ā —Ä–ĺ—Ā—ā–ĺ–ľ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č –ī–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ—Ź—Ź —ć–Ĺ–Ķ—Ä–≥–ł—Ź –į—Ā–ł–ľ–Ņ—ā–ĺ—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ł–Ī–Ľ–ł–∂–į–Ķ—ā—Ā—Ź –ļ –ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–ľ—É (–≥—Ä–į–Ĺ–ł—á–Ĺ–ĺ–ľ—É) –∑–Ĺ–į—á–Ķ–Ĺ–ł—é, –ł, –Ķ—Ā–Ľ–ł —Ā–ĺ–ĺ–Ī—Č–ł—ā—Ć —ć—ā–ł–ľ —Ā–ł—Ā—ā–Ķ–ľ–į–ľ —ć–Ĺ–Ķ—Ä–≥–ł—é –Ņ—Ä–Ķ–≤—č—ą–į—é—Č—É—é —ā—É, —á—ā–ĺ —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤—É–Ķ—ā –≥—Ä–į–Ĺ–ł—á–Ĺ–ĺ–ľ—É –∑–Ĺ–į—á–Ķ–Ĺ–ł—é, —ā–ĺ —ć—ā–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–Ķ—ā –Ņ–ĺ–Ľ—É—á–ł—ā—Ć —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ņ—Ä–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ —Ā–ł—Ā—ā–Ķ–ľ–į –Ĺ–Ķ —Ö–ĺ–Ľ–ĺ–ī–Ĺ–Ķ–Ķ, —á–Ķ–ľ –Ņ—Ä–ł  –į –≥–ĺ—Ä—Ź—á–Ķ–Ķ, —á–Ķ–ľ –Ņ—Ä–ł –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ
–į –≥–ĺ—Ä—Ź—á–Ķ–Ķ, —á–Ķ–ľ –Ņ—Ä–ł –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ķ  –ė–Ĺ–į—á–Ķ –≥–ĺ–≤–ĺ—Ä—Ź, –ĺ–Ī–Ľ–į—Ā—ā—Ć –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –Ĺ–į —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–Ļ —ą–ļ–į–Ľ–Ķ –Ľ–Ķ–∂–ł—ā –Ĺ–Ķ –Ĺ–ł–∂–Ķ
–ė–Ĺ–į—á–Ķ –≥–ĺ–≤–ĺ—Ä—Ź, –ĺ–Ī–Ľ–į—Ā—ā—Ć –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –Ĺ–į —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–Ļ —ą–ļ–į–Ľ–Ķ –Ľ–Ķ–∂–ł—ā –Ĺ–Ķ –Ĺ–ł–∂–Ķ  –į –≤—č—ą–Ķ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –≤ –Ņ–ĺ—Ä—Ź–ī–ļ–Ķ —Ä–ĺ—Ā—ā–į —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į
–į –≤—č—ą–Ķ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä. –Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –≤ –Ņ–ĺ—Ä—Ź–ī–ļ–Ķ —Ä–ĺ—Ā—ā–į —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į  –Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —Ā–≤–ĺ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –Ņ–ĺ —ą–ļ–į–Ľ–Ķ –≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł:
–Ņ—Ä–ĺ—Ö–ĺ–ī–ł—ā —Ā–≤–ĺ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –Ņ–ĺ —ą–ļ–į–Ľ–Ķ –≤ —Ā–Ľ–Ķ–ī—É—é—Č–Ķ–Ļ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł:
 ,
, 
 ,...
,...  , ...,
, ..., .
.
–ö–į–∂—É—Č–į—Ź—Ā—Ź –Ĺ–Ķ–Ľ–Ķ–Ņ–ĺ—Ā—ā—Ć —ā–į–ļ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–Ļ —ą–ļ–į–Ľ—č –ĺ–Ī—ä—Ź—Ā–Ĺ—Ź–Ķ—ā—Ā—Ź —Ā–Ľ—É—á–į–Ļ–Ĺ—č–ľ –≤—č–Ī–ĺ—Ä–ĺ–ľ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł. –ē—Ā–Ľ–ł –Ī—č –ĺ–Ĺ–į –Ī—č–Ľ–į –≤—č–Ī—Ä–į–Ĺ–į –≤ –≤–ł–ī–Ķ  , —ā–ĺ —Ā–į–ľ—č–Ķ –Ĺ–ł–∑–ļ–ł–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ĺ–≤–į–Ľ–ł
, —ā–ĺ —Ā–į–ľ—č–Ķ –Ĺ–ł–∑–ļ–ł–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ĺ–≤–į–Ľ–ł  , –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č ‚ĒÄ –Ĺ—É–Ľ—é, –į –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ĺ–≤–į–Ľ–ł –Ī—č –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź–ľ —ć—ā–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ł–Ļ –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —Ö–ĺ–ī–į –Ņ–ĺ —ą–ļ–į–Ľ–Ķ –ĺ—ā –ľ–Ķ–Ĺ—Ć—ą–Ķ–≥–ĺ –ļ –Ī–ĺ–Ľ—Ć—ą–Ķ–ľ—É –Ī—č–Ľ –Ī—č –≤–ĺ—Ā—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ. [43]. [44].
, –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ—č–Ķ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č ‚ĒÄ –Ĺ—É–Ľ—é, –į –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–ĺ–≤–į–Ľ–ł –Ī—č –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č–ľ –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź–ľ —ć—ā–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–Ĺ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ –į–Ľ–≥–Ķ–Ī—Ä–į–ł—á–Ķ—Ā–ļ–ł–Ļ –Ņ–ĺ—Ä—Ź–ī–ĺ–ļ —Ö–ĺ–ī–į –Ņ–ĺ —ą–ļ–į–Ľ–Ķ –ĺ—ā –ľ–Ķ–Ĺ—Ć—ą–Ķ–≥–ĺ –ļ –Ī–ĺ–Ľ—Ć—ą–Ķ–ľ—É –Ī—č–Ľ –Ī—č –≤–ĺ—Ā—Ā—ā–į–Ĺ–ĺ–≤–Ľ–Ķ–Ĺ. [43]. [44].
–ě–Ī—Č–ł–Ķ –≤—č–≤–ĺ–ī—č, –ļ–ĺ—ā–ĺ—Ä—č–Ķ –ľ–ĺ–∂–Ĺ–ĺ —Ā–ī–Ķ–Ľ–į—ā—Ć –ĺ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź—Ö —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł:
1. –ě–Ī–Ľ–į—Ā—ā—Ć —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł–Ļ —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł –Ľ–Ķ–∂–ł—ā –Ĺ–į–ī –ĺ–Ī–Ľ–į—Ā—ā—Ć—é –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä.
2. –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź ¬ę—Ä–į–Ī–ĺ—ā—謼, ¬ę—ā–Ķ–Ņ–Ľ–į¬Ľ , ¬ę–Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–≥–嬼 –ł ¬ę–ľ–Ķ–Ĺ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–≥–嬼 —ā–Ķ–Ľ–į –ĺ—Ā—ā–į—é—ā—Ā—Ź –≤ —Ā–ł–Ľ–Ķ, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ņ—Ä–ł  –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā—č–ľ —ā–Ķ–Ľ–ĺ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–Ķ–Ľ–ĺ , –ł–ľ–Ķ—é—Č–Ķ–Ķ –Ī–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ—É—é –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—É—é —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—É , —ā–ĺ –Ķ—Ā—ā—Ć –ľ–Ķ–Ĺ—Ć—ą—É—é –Ņ–ĺ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–Ķ.
–Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā—č–ľ —ā–Ķ–Ľ–ĺ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–Ķ–Ľ–ĺ , –ł–ľ–Ķ—é—Č–Ķ–Ķ –Ī–ĺ–Ľ–Ķ–Ķ –≤—č—Ā–ĺ–ļ—É—é –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—É—é —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—É , —ā–ĺ –Ķ—Ā—ā—Ć –ľ–Ķ–Ĺ—Ć—ą—É—é –Ņ–ĺ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ–Ļ –≤–Ķ–Ľ–ł—á–ł–Ĺ–Ķ.
3. –°—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ –ĺ—ā–Ľ–ł—á–ł–Ķ–ľ —Ā–ł—Ā—ā–Ķ–ľ —Ā  –ĺ—ā —Ā–ł—Ā—ā–Ķ–ľ —Ā
–ĺ—ā —Ā–ł—Ā—ā–Ķ–ľ —Ā  —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ, —á—ā–ĺ –≤ —Ā–ł—Ā—ā–Ķ–ľ–į—Ö –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä —ā–Ķ–Ņ–Ľ–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –≤ —Ä–į–Ī–ĺ—ā—É —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ, –Ī–Ķ–∑ –≤—Ā—Ź–ļ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł, –į —Ä–į–Ī–ĺ—ā–į –Ņ—Ä–Ķ–≤—Ä–į—Č–į–Ķ—ā—Ā—Ź –≤ —ā–Ķ–Ņ–Ľ–ĺ —ā–ĺ–Ľ—Ć–ļ–ĺ —Ā –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–Ķ–Ļ.
—Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā–ĺ, —á—ā–ĺ –≤ —Ā–ł—Ā—ā–Ķ–ľ–į—Ö –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä —ā–Ķ–Ņ–Ľ–ĺ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –≤ —Ä–į–Ī–ĺ—ā—É —Ā–į–ľ–ĺ–Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ—Ć–Ĺ–ĺ, –Ī–Ķ–∑ –≤—Ā—Ź–ļ–ĺ–Ļ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł, –į —Ä–į–Ī–ĺ—ā–į –Ņ—Ä–Ķ–≤—Ä–į—Č–į–Ķ—ā—Ā—Ź –≤ —ā–Ķ–Ņ–Ľ–ĺ —ā–ĺ–Ľ—Ć–ļ–ĺ —Ā –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–Ķ–Ļ.
4. –ü–Ķ—Ä–≤–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ļ–į–ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ–Ķ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ā–ł—Ā—ā–Ķ–ľ —Ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł —Ā–ĺ—Ö—Ä–į–Ĺ—Ź–Ķ—ā —Ā–≤–ĺ—Ď –į–Ĺ–į–Ľ–ł—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ. –°–ĺ—Ö—Ä–į–Ĺ—Ź–Ķ—ā—Ā—Ź —ā–į–ļ–∂–Ķ –į–Ĺ–į–Ľ–ł—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –≤ –≤–ł–ī–Ķ

5. –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ, —Ā—Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ–ĺ–Ķ –ö–Ľ–į—É–∑–ł—É—Ā–ĺ–ľ, —Ā–ĺ—Ö—Ä–į–Ĺ—Ź–Ķ—ā —Ā–≤–ĺ—é —Ā–ł–Ľ—É, —ā–į–ļ –ļ–į–ļ –ł –Ņ—Ä–ł  –ł –Ņ—Ä–ł
–ł –Ņ—Ä–ł  —ā–Ķ–Ņ–Ľ–ĺ —Ā–į–ľ–ĺ —Ā–ĺ–Ī–ĺ–Ļ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –ľ–Ķ–Ĺ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–ľ—É, —ā–ĺ –Ķ—Ā—ā—Ć –ĺ—ā —ā–Ķ–Ľ–į —Ā –Ī–ĺ–Ľ—Ć—ą–Ķ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ –ļ —ā–Ķ–Ľ—É —Ā –ľ–Ķ–Ĺ—Ć—ą–Ķ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ.
—ā–Ķ–Ņ–Ľ–ĺ —Ā–į–ľ–ĺ —Ā–ĺ–Ī–ĺ–Ļ –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–ł—ā –ĺ—ā –Ī–ĺ–Ľ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–≥–ĺ —ā–Ķ–Ľ–į –ļ –ľ–Ķ–Ĺ–Ķ–Ķ –Ĺ–į–≥—Ä–Ķ—ā–ĺ–ľ—É, —ā–ĺ –Ķ—Ā—ā—Ć –ĺ—ā —ā–Ķ–Ľ–į —Ā –Ī–ĺ–Ľ—Ć—ą–Ķ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ –ļ —ā–Ķ–Ľ—É —Ā –ľ–Ķ–Ĺ—Ć—ą–Ķ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ.
6. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł —Ā–ĺ–∑–ī–į–Ĺ–ł—Ź –≤–Ķ—á–Ĺ–ĺ–≥–ĺ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į —ā–į–ļ–∂–Ķ —Ā–ĺ—Ö—Ä–į–Ĺ—Ź–Ķ—ā —Ā–≤–ĺ—é —Ā–ł–Ľ—É –Ņ–ĺ—Ā–Ľ–Ķ –≤–Ĺ–Ķ—Ā–Ķ–Ĺ–ł—Ź –≤ –Ĺ–Ķ—Ď —É—ā–ĺ—á–Ĺ–Ķ–Ĺ–ł—Ź: –≤–Ķ—á–Ĺ—č–Ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ķ–Ĺ, –Ņ—Ä–ł—á—Ď–ľ —ć—ā–ĺ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź –≤ —Ā–Ľ—É—á–į–Ķ –ĺ–Ī—č—á–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ —Ā  –ł –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł–Ķ –ī–Ľ—Ź –Ĺ–Ķ–ĺ–Ī—č—á–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ —Ā
–ł –ī–ĺ–Ņ—É—Ā–ļ–į–Ķ—ā –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł–Ķ –ī–Ľ—Ź –Ĺ–Ķ–ĺ–Ī—č—á–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ —Ā  . –Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź –ĺ –≤–Ķ—á–Ĺ–ĺ–ľ –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į –ĺ–∑–Ĺ–į—á–į–Ķ—ā, —á—ā–ĺ –Ķ—Ā–Ľ–ł —ā–Ķ–Ņ–Ľ–ĺ –Ĺ–Ķ–Ľ—Ć–∑—Ź –Ņ—Ä–Ķ–≤—Ä–į—ā–ł—ā—Ć –≤ —Ä–į–Ī–ĺ—ā—É –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ī–Ķ–∑ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł, —ā–ĺ —Ä–į–Ī–ĺ—ā—É –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–Ķ–≤—Ä–į—ā–ł—ā—Ć –≤ —ā–Ķ–Ņ–Ľ–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ī–Ķ–∑ –≤—Ā—Ź–ļ–ł—Ö –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–Ļ. [45].
. –Ě–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –ĺ–Ī—Ä–į—Č–Ķ–Ĺ–ł—Ź —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł—Ź –ĺ –≤–Ķ—á–Ĺ–ĺ–ľ –ī–≤–ł–≥–į—ā–Ķ–Ľ–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į –ĺ–∑–Ĺ–į—á–į–Ķ—ā, —á—ā–ĺ –Ķ—Ā–Ľ–ł —ā–Ķ–Ņ–Ľ–ĺ –Ĺ–Ķ–Ľ—Ć–∑—Ź –Ņ—Ä–Ķ–≤—Ä–į—ā–ł—ā—Ć –≤ —Ä–į–Ī–ĺ—ā—É –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ī–Ķ–∑ –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł, —ā–ĺ —Ä–į–Ī–ĺ—ā—É –ľ–ĺ–∂–Ĺ–ĺ –Ņ—Ä–Ķ–≤—Ä–į—ā–ł—ā—Ć –≤ —ā–Ķ–Ņ–Ľ–ĺ –Ņ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—Ć—é –Ī–Ķ–∑ –≤—Ā—Ź–ļ–ł—Ö –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–Ļ. [45].
7. –ü–ĺ—Ā—ā—É–Ľ–į—ā –ö–į—Ä–į—ā–Ķ–ĺ–ī–ĺ—Ä–ł ‚ĒÄ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ĺ –Ĺ–Ķ–ī–ĺ—Ā—ā–ł–∂–ł–ľ–ĺ—Ā—ā–ł ‚ĒÄ —ā–į–ļ–∂–Ķ —Ā–ĺ—Ö—Ä–į–Ĺ—Ź–Ķ—ā —Ā–≤–ĺ—é —Ā–ł–Ľ—É.
8. –§–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į ‚ĒÄ –ü–Ľ–į–Ĺ–ļ–į –Ņ–Ķ—Ä–Ķ—Ā—ā–į—Ď—ā –Ī—č—ā—Ć —Ā–Ņ—Ä–į–≤–Ķ–ī–Ľ–ł–≤–ĺ–Ļ –Ņ—Ä–ł  , –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –≤ –ĺ–Ī–Ľ–į—Ā—ā–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –ľ–ĺ–∂–Ĺ–ĺ –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–ł—ā—Ć –≤–Ķ—á–Ĺ—č–Ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į, —ā–ĺ –Ķ—Ā—ā—Ć —ā–į–ļ–ĺ–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ķ–Ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć —Ä–į–Ī–ĺ—ā—É —ā–ĺ–Ľ—Ć–ļ–ĺ –∑–į —Ā—á—Ď—ā –ĺ—Ö–Ľ–į–∂–ī–Ķ–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ–≥–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į —ā–Ķ–Ņ–Ľ–į –Ī–Ķ–∑ –ļ–į–ļ–ł—Ö‚Äď–Ľ–ł–Ī–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ļ –≤ –ī—Ä—É–≥–ł—Ö —ā–Ķ–Ľ–į—Ö.
, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –≤ –ĺ–Ī–Ľ–į—Ā—ā–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –ľ–ĺ–∂–Ĺ–ĺ –ĺ—Ā—É—Č–Ķ—Ā—ā–≤–ł—ā—Ć –≤–Ķ—á–Ĺ—č–Ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć –≤—ā–ĺ—Ä–ĺ–≥–ĺ —Ä–ĺ–ī–į, —ā–ĺ –Ķ—Ā—ā—Ć —ā–į–ļ–ĺ–Ļ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ķ–Ĺ –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–ł—ā—Ć —Ä–į–Ī–ĺ—ā—É —ā–ĺ–Ľ—Ć–ļ–ĺ –∑–į —Ā—á—Ď—ā –ĺ—Ö–Ľ–į–∂–ī–Ķ–Ĺ–ł—Ź –ĺ–ī–Ĺ–ĺ–≥–ĺ –ł—Ā—ā–ĺ—á–Ĺ–ł–ļ–į —ā–Ķ–Ņ–Ľ–į –Ī–Ķ–∑ –ļ–į–ļ–ł—Ö‚Äď–Ľ–ł–Ī–ĺ –ł–∑–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ļ –≤ –ī—Ä—É–≥–ł—Ö —ā–Ķ–Ľ–į—Ö.
9. –Ě–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł—ā —ā–į–ļ–∂–Ķ –Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ĺ–į—á–į–Ľ—É —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –≤—ā–ĺ—Ä–ĺ–ľ—É –Ĺ–į—á–į–Ľ—É —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ĺ–Ī–Ľ–į—Ā—ā–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä ( ), –ĺ–ī–Ĺ–į–ļ–ĺ –≤ —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –Ĺ—É–∂–Ĺ–ĺ –ł–Ľ–ł –ł—Ā–ļ–Ľ—é—á–ł—ā—Ć –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź –ĺ–Ī–Ľ–į—Ā—ā–Ķ–Ļ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –ł–Ľ–ł –ĺ—ā–ļ–į–∑–į—ā—Ć—Ā—Ź –ĺ—ā –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –≤ —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź —ć—ā–ł—Ö –ĺ–Ī–Ľ–į—Ā—ā–Ķ–Ļ (—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ V –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł ‚ÄĒ —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–Ķ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į). [44].
), –ĺ–ī–Ĺ–į–ļ–ĺ –≤ —ć—ā–ĺ–ľ —Ā–Ľ—É—á–į–Ķ –Ĺ—É–∂–Ĺ–ĺ –ł–Ľ–ł –ł—Ā–ļ–Ľ—é—á–ł—ā—Ć –≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—Ć –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź –ĺ–Ī–Ľ–į—Ā—ā–Ķ–Ļ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä –ł–Ľ–ł –ĺ—ā–ļ–į–∑–į—ā—Ć—Ā—Ź –ĺ—ā –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –≤ —É—Ā–Ľ–ĺ–≤–ł—Ź—Ö –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–ł—Ź —ć—ā–ł—Ö –ĺ–Ī–Ľ–į—Ā—ā–Ķ–Ļ (—Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ V –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ—Ā—ā–į—ā–ł–ļ–ł ‚ÄĒ —ā–Ķ–ĺ—Ä–Ķ–ľ–į –ļ–ĺ–ľ–Ņ–Ķ–Ĺ—Ā–į—Ü–ł–ł –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–Ķ–≥–ĺ —ā–Ķ–Ņ–Ľ–ĺ–ĺ–Ī–ľ–Ķ–Ĺ–į). [44].
10. –ē—Č—Ď –ĺ–ī–Ĺ–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ —Ā–ł—Ā—ā–Ķ–ľ —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ –∑–į–ļ–Ľ—é—á–į–Ķ—ā—Ā—Ź –≤ —ā–ĺ–ľ, —á—ā–ĺ –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ —Ā–ĺ–≤–Ķ—Ä—ą–ł—ā—Ć –ĺ–Ī—Ä–į—ā–ł–ľ—č–Ļ —Ü–ł–ļ–Ľ –ö–į—Ä–Ĺ–ĺ –ľ–Ķ–∂–ī—É —ā–Ķ–Ľ–į–ľ–ł (—Ā–ł—Ā—ā–Ķ–ľ–į–ľ–ł) —Ā —Ä–į–∑–Ĺ—č–ľ–ł –∑–Ĺ–į–ļ–į–ľ–ł, —ā–į–ļ –ļ–į–ļ –ī–Ľ—Ź —ć—ā–ĺ–≥–ĺ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ĺ –ĺ–Ī—Ä–į—ā–ł–ľ–ĺ –Ņ—Ä–ĺ–Ļ—ā–ł —á–Ķ—Ä–Ķ–∑ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ –Ī–ĺ–Ľ—Ć—ą–ł–Ķ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä—č, —á—ā–ĺ –Ĺ–Ķ–ĺ—Ā—É—Č–Ķ—Ā—ā–≤–ł–ľ–ĺ. –ü–Ķ—Ä–Ķ—Ö–ĺ–ī –≤ —Ā–ĺ—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–ĺ–Ļ –≤ –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć —ā–ĺ–Ľ—Ć–ļ–ĺ –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ–≤–Ķ—Ā–Ĺ—č–ľ. [46]
–ď—Ä–į–Ĺ–ł—Ü—č –Ņ—Ä–ł–ľ–Ķ–Ĺ–ł–ľ–ĺ—Ā—ā–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł
–í —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ł–ī–Ķ–Ļ –ö–Ľ–į—É–∑–ł—É—Ā–į –ł –Ķ–≥–ĺ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ķ–Ļ –ĺ–Ī–į –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ĺ—Ā–Ĺ–ĺ–≤—č–≤–į—é—ā—Ā—Ź –Ĺ–į –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–Ķ –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł (–Ņ–ĺ—Ā—ā—É–Ľ–į—ā—č –ö–Ľ–į—É–∑–ł—É—Ā–į, –Ę–ĺ–ľ—Ā–ĺ–Ĺ–į-–ö–Ķ–Ľ—Ć–≤–ł–Ĺ–į, –ü–Ľ–į–Ĺ–ļ–į –ł –ī—Ä.), –Ņ—Ä–ł—á—Ď–ľ –≤–ĺ –≥–Ľ–į–≤—É —É–≥–Ľ–į –Ņ–ĺ—Ā—ā–į–≤–Ľ–Ķ–Ĺ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –ļ–ĺ—ā–ĺ—Ä—č–Ļ –≤–ĺ–∑–≤–ĺ–ī–ł—ā—Ā—Ź –≤ —Ä–į–Ĺ–≥ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī—č, —Ā—ā–ĺ—Ź—Č–Ķ–≥–ĺ —Ä—Ź–ī–ĺ–ľ —Ā –∑–į–ļ–ĺ–Ĺ–ĺ–ľ —Ā–ĺ—Ö—Ä–į–Ĺ–Ķ–Ĺ–ł—Ź —ć–Ĺ–Ķ—Ä–≥–ł–ł. –ź–Ī—Ā–ĺ–Ľ—é—ā–ł–∑–į—Ü–ł—Ź –ö–Ľ–į—É–∑–ł—É—Ā–ĺ–ľ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ņ—Ä–ł–ĺ–Ī—Ä–Ķ–Ľ–į —Ā–ľ—č—Ā–Ľ –≤–į–∂–Ĺ–Ķ–Ļ—ą–Ķ–≥–ĺ –ļ–ĺ—Ā–ľ–ĺ–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī—č, —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ķ–ľ –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ —Ā—ā–į–Ľ–į –į–Ĺ—ā–ł–Ĺ–į—É—á–Ĺ–į—Ź –ļ–ĺ–Ĺ—Ü–Ķ–Ņ—Ü–ł—Ź ¬ę—ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —Ā–ľ–Ķ—Ä—ā–ł –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ¬Ľ[47]. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ľ—é–Ī–ĺ–Ķ –Ĺ–į—Ä—É—ą–Ķ–Ĺ–ł–Ķ —ć—ā–ĺ–≥–ĺ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į –Ņ—Ä–ł–≤–Ķ–Ľ–ĺ –Ī—č –ļ –ĺ–Ī—Ä—É—ą–Ķ–Ĺ–ł—é –≤—Ā–Ķ—Ö —Ā–Ľ–Ķ–ī—Ā—ā–≤–ł–Ļ –ł–∑ –Ĺ–Ķ–≥–ĺ, —á—ā–ĺ —Ā—É—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ –ĺ–≥—Ä–į–Ĺ–ł—á–ł–Ľ–ĺ –Ī—č —Ā—Ą–Ķ—Ä—É –≤–Ľ–ł—Ź–Ĺ–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –•–į—Ä–į–ļ—ā–Ķ—Ä–Ĺ—č–ľ –≤ —ć—ā–ĺ–ľ —Ā–ľ—č—Ā–Ľ–Ķ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤—č—Ā–ļ–į–∑—č–≤–į–Ĺ–ł–Ķ –ú. –ü–Ľ–į–Ĺ–ļ–į, —É—ā–≤–Ķ—Ä–∂–ī–į–≤—ą–Ķ–≥–ĺ, —á—ā–ĺ —Ā –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā—Ć—é ¬ę—Ā—ā–ĺ–ł—ā –ł –Ņ–į–ī–į–Ķ—ā —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į¬Ľ. –í —ć—ā–ĺ–ľ —Ā–ľ—č—Ā–Ľ–Ķ –≤—č–≤–ĺ–ī—č —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł –ĺ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–Ĺ–ĺ–ľ —Ö–į—Ä–į–ļ—ā–Ķ—Ä–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł –ł –ĺ—ā–ļ—Ä—č—ā–ł–Ķ —Ā–ł—Ā—ā–Ķ–ľ —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ–ł –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č–ľ–ł —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į–ľ–ł –ī–ĺ–Ľ–∂–Ĺ—č –Ņ—Ä–ł–≤–Ķ—Ā—ā–ł –ļ –ļ—Ä–į—Ö—É –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į, –į –≤–ľ–Ķ—Ā—ā–Ķ —Ā –Ĺ–ł–ľ –ł —Ā–į–ľ–ĺ–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –ě–ī–Ĺ–į–ļ–ĺ —ć—ā–ĺ –Ĺ–Ķ –Ņ—Ä–ĺ–ł–∑–ĺ—ą–Ľ–ĺ.
–ě—ą–ł–Ī–ĺ—á–Ĺ—č–Ļ –≤—č–≤–ĺ–ī –ú. –ü–Ľ–į–Ĺ–ļ–į –ĺ ¬ę–Ņ–į–ī–Ķ–Ĺ–ł–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł¬Ľ —Ā –Ņ–į–ī–Ķ–Ĺ–ł–Ķ–ľ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā–į –Ĺ–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā–ł –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ā–≤—Ź–∑–į–Ĺ —Ā —Ā–Ľ–ĺ–∂–ł–≤—ą–ł–ľ—Ā—Ź –ł—Ā—ā–ĺ—Ä–ł—á–Ķ—Ā–ļ–ł, –ĺ–Ī—ä–Ķ–ī–ł–Ĺ–Ķ–Ĺ–ł–ł –≤ –ĺ–ī–Ĺ–ĺ–ľ –∑–į–ļ–ĺ–Ĺ–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–≤ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł –Ņ—Ä–ł–ī–į–Ĺ–ł–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—É –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł —Ā–ľ—č—Ā–Ľ–į –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –Ě–į –Ĺ–Ķ—Ä–į–≤–Ĺ–ĺ—Ü–Ķ–Ĺ–Ĺ–ĺ—Ā—ā—Ć —É–ļ–į–∑–į–Ĺ–Ĺ—č—Ö –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–≤ –ł –Ĺ–Ķ—Ā–ĺ–≤–ľ–Ķ—Ā—ā–ł–ľ–ĺ—Ā—ā—Ć –ł—Ö –≤ –ĺ–ī–Ĺ–ĺ–ľ –Ĺ–į—á–į–Ľ–Ķ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ĺ–Ī—Ä–į—ā–ł–Ľ–į –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ
–Ę. –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–į-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā. –ü–ĺ –Ķ—Ď —Ā–Ľ–ĺ–≤–į–ľ, –ĺ–ī–Ĺ–ĺ –ł —ā–ĺ –∂–Ķ –Ĺ–į—á–į–Ľ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā—Ā—Ź –≤ –ī–≤—É—Ö —Ā–ĺ–≤–Ķ—Ä—ą–Ķ–Ĺ–Ĺ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö –ĺ–Ī–Ľ–ł–ļ–į—Ö:
1. –ö–į–ļ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –ł–Ĺ—ā–Ķ–≥—Ä–ł—Ä—É—é—Č–Ķ–≥–ĺ –ľ–Ĺ–ĺ–∂–ł—ā–Ķ–Ľ—Ź –ī–Ľ—Ź –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ–≥–ĺ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź 
2. –ö–į–ļ —É—ā–≤–Ķ—Ä–∂–ī–Ķ–Ĺ–ł–Ķ –ĺ –Ĺ–Ķ—É–ļ–Ľ–ĺ–Ĺ–Ĺ–ĺ–ľ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ņ—Ä–ł —Ä–Ķ–į–Ľ—Ć–Ĺ—č—Ö –į–ī–ł–į–Ī–į—ā–ł—á–Ķ—Ā–ļ–ł—Ö –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į—Ö. –ü—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā—Ā—Ź —ā—Ä—É–ī–Ĺ—č–ľ —É–ľ–Ķ—Ā—ā–ł—ā—Ć –≤ –ĺ–ī–Ĺ–ĺ –ĺ—ā—á–Ķ—ā–Ľ–ł–≤–ĺ–Ķ –ĺ–Ī–ĺ–∑—Ä–ł–ľ–ĺ–Ķ –Ņ–ĺ–Ľ–Ķ –∑—Ä–Ķ–Ĺ–ł—Ź —ć—ā–ł –ĺ–Ī–į –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ł —Ā—Ö–≤–į—ā–ł—ā—Ć –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ–Ķ —ā–ĺ–∂–ī–Ķ—Ā—ā–≤–ĺ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į –ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–į –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł[48].
–Ď–Ľ–į–≥–ĺ–ī–į—Ä—Ź —Ä–Ķ–≤–ł–∑–ł–ł –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –Ĺ–į –Ņ–Ķ—Ä–≤—č–Ļ –Ņ–Ľ–į–Ĺ –≤ –ļ–į—á–Ķ—Ā—ā–≤–Ķ —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –≤—č—Ö–ĺ–ī–ł—ā –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, –į –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–ľ –Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ—č–ľ, —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ł–ľ, –ļ–ĺ—ā–ĺ—Ä—č–Ļ, –Ņ–ĺ —Ā–Ľ–ĺ–≤–į–ľ –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–ĺ–Ļ-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā, –≤—č–Ņ–ĺ–Ľ–Ĺ—Ź–Ķ—ā—Ā—Ź ¬ę—ā–ĺ–Ľ—Ć–ļ–ĺ –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä—č–Ķ —ć–Ņ–ĺ—Ö–ł¬Ľ.[49]
–ď–ł–Ņ–ĺ—ā–Ķ–∑–į ¬ę—ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —Ā–ľ–Ķ—Ä—ā–ł –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ¬Ľ
–Ě–Ķ–ļ—Ä–ł—ā–ł—á–Ķ—Ā–ļ–ĺ–Ķ –ĺ–Ī–ĺ–Ī—Č–Ķ–Ĺ–ł–Ķ –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–Ķ–Ļ –∑–Ķ–ľ–Ĺ–ĺ–≥–ĺ –ĺ–Ņ—č—ā–į, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, —Ä–į—Ā–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł–Ķ –≤—č–≤–ĺ–ī–ĺ–≤ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ĺ –≤–ĺ–∑—Ä–į—Ā—ā–į–Ĺ–ł–ł —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –ł–∑–ĺ–Ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ—č –≥–į–Ľ–į–ļ—ā–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ —Ä–į–∑–ľ–Ķ—Ä–į, –≥–ī–Ķ –∑–Ĺ–į—á–ł—ā–Ķ–Ľ—Ć–Ĺ—É—é —Ä–ĺ–Ľ—Ć –≤ —Ą–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–ł–ł –Ĺ–ĺ–≤—č—Ö –∑–≤—Ď–∑–ī–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ –ł–≥—Ä–į—é—ā –≥—Ä–į–≤–ł—ā–į—Ü–ł–ĺ–Ĺ–Ĺ—č–Ķ —Ā–ł–Ľ—č, –ł –Ĺ–į –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ—É—é –≤ —Ü–Ķ–Ľ–ĺ–ľ –Ņ—Ä–ł–≤–ĺ–ī–ł–Ľ–ĺ –≤ –Ņ—Ä–ĺ—ą–Ľ–ĺ–ľ –ļ –į–Ĺ—ā–ł–Ĺ–į—É—á–Ĺ–ĺ–ľ—É –≤—č–≤–ĺ–ī—É –ĺ ¬ę—ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —Ā–ľ–Ķ—Ä—ā–ł –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ¬Ľ. –°–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ—č–ľ –ī–į–Ĺ–Ĺ—č–ľ –ú–Ķ—ā–į–≥–į–Ľ–į–ļ—ā–ł–ļ–į –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ—ā —Ā–ĺ–Ī–ĺ–Ļ —Ä–į—Ā—ą–ł—Ä—Ź—é—Č—É—é—Ā—Ź —Ā–ł—Ā—ā–Ķ–ľ—É, –ļ–ĺ—ā–ĺ—Ä–į—Ź —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ—Ā—ā–į—Ü–ł–ĺ–Ĺ–į—Ä–Ĺ–ĺ–Ļ, –ł –Ņ–ĺ—ć—ā–ĺ–ľ—É –≤–ĺ–Ņ—Ä–ĺ—Ā –ĺ —ā–Ķ–Ņ–Ľ–ĺ–≤–ĺ–Ļ —Ā–ľ–Ķ—Ä—ā–ł –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ĺ–Ķ–Ľ—Ć–∑—Ź –ī–į–∂–Ķ —Ā—ā–į–≤–ł—ā—Ć[50].
–ě–ī–Ĺ–į–ļ–ĺ —Ā–į–ľ —ā–Ķ—Ä–ľ–ł–Ĺ ¬ę—ā–Ķ–Ņ–Ľ–ĺ–≤–į—Ź —Ā–ľ–Ķ—Ä—ā—Ć –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ¬Ľ –ł–Ĺ–ĺ–≥–ī–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –ī–Ľ—Ź –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź —Ā—Ü–Ķ–Ĺ–į—Ä–ł—Ź –Ī—É–ī—É—Č–Ķ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł—Ź –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, —Ā–ĺ–≥–Ľ–į—Ā–Ĺ–ĺ –ļ–ĺ—ā–ĺ—Ä–ĺ–ľ—É –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–į—Ź —ā–į–ļ –ł –Ī—É–ī–Ķ—ā —Ä–į—Ā—ą–ł—Ä—Ź—ā—Ć—Ā—Ź –ī–ĺ –Ī–Ķ—Ā–ļ–ĺ–Ĺ–Ķ—á–Ĺ–ĺ—Ā—ā–ł –≤–ĺ —ā—Ć–ľ—É –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–į, –Ņ–ĺ–ļ–į –Ĺ–Ķ –ĺ–Ī—Ä–į—ā–ł—ā—Ā—Ź –≤ —Ä–į—Ā—Ā–Ķ—Ź–Ĺ–Ĺ—č–Ļ —Ö–ĺ–Ľ–ĺ–ī–Ĺ—č–Ļ –Ņ—Ä–į—Ö.
–í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł (–≤ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–Ķ –Ĺ–Ķ—É–Ī—č–≤–į–Ĺ–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł) –ł–Ĺ–ĺ–≥–ī–į –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É–Ķ—ā—Ā—Ź –ļ—Ä–ł—ā–ł–ļ–į–ľ–ł —ć–≤–ĺ–Ľ—é—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–Ļ —ā–Ķ–ĺ—Ä–ł–ł —Ā —Ü–Ķ–Ľ—Ć—é –Ņ–ĺ–ļ–į–∑–į—ā—Ć, —á—ā–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ –Ņ—Ä–ł—Ä–ĺ–ī—č –≤ —Ā—ā–ĺ—Ä–ĺ–Ĺ—É —É—Ā–Ľ–ĺ–∂–Ĺ–Ķ–Ĺ–ł—Ź –Ĺ–Ķ–≤–ĺ–∑–ľ–ĺ–∂–Ĺ–ĺ. –ě–ī–Ĺ–į–ļ–ĺ –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ–Ķ –Ņ—Ä–ł–ľ–Ķ–Ĺ–Ķ–Ĺ–ł–Ķ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –Ĺ–Ķ–ļ–ĺ—Ä—Ä–Ķ–ļ—ā–Ĺ—č–ľ, —ā–į–ļ –ļ–į–ļ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł—Ź –Ĺ–Ķ —É–Ī—č–≤–į–Ķ—ā —ā–ĺ–Ľ—Ć–ļ–ĺ –≤ –∑–į–ľ–ļ–Ĺ—É—ā—č—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö (—Ā—Ä–į–≤–Ĺ. —Ā –ī–ł—Ā—Ā–ł–Ņ–į—ā–ł–≤–Ĺ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–ĺ–Ļ), –≤ —ā–ĺ –≤—Ä–Ķ–ľ—Ź –ļ–į–ļ –∂–ł–≤—č–Ķ –ĺ—Ä–≥–į–Ĺ–ł–∑–ľ—č –ł –Ņ–Ľ–į–Ĺ–Ķ—ā–į –ó–Ķ–ľ–Ľ—Ź –≤ —Ü–Ķ–Ľ–ĺ–ľ —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ĺ—ā–ļ—Ä—č—ā—č–ľ–ł —Ā–ł—Ā—ā–Ķ–ľ–į–ľ–ł. [51], [52].
–í –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–Ķ –∂–ł–∑–Ĺ–Ķ–ī–Ķ—Ź—ā–Ķ–Ľ—Ć–Ĺ–ĺ—Ā—ā–ł –∂–ł–≤—č–Ķ –ĺ—Ä–≥–į–Ĺ–ł–∑–ľ—č –Ņ—Ä–Ķ–≤—Ä–į—Č–į—é—ā —ć–Ĺ–Ķ—Ä–≥–ł—é –ĺ–ī–Ĺ–ĺ–≥–ĺ –≤–ł–ī–į (—ć–Ľ–Ķ–ļ—ā—Ä–ĺ–ľ–į–≥–Ĺ–ł—ā–Ĺ—É—é —Ā–ĺ–Ľ–Ĺ–Ķ—á–Ĺ—É—é, —Ö–ł–ľ–ł—á–Ķ—Ā–ļ—É—é) –≤ —ć–Ĺ–Ķ—Ä–≥–ł—é –ī—Ä—É–≥–ĺ–≥–ĺ –≤–ł–ī–į (—ā–Ķ–Ņ–Ľ–ĺ–≤—É—é), —ā–Ķ–ľ —Ā–į–ľ—č–ľ —É—Ā–ļ–ĺ—Ä—Ź—Ź —Ā—É–ľ–ľ–į—Ä–Ĺ–ĺ–Ķ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ. –Ě–Ķ—Ā–ľ–ĺ—ā—Ä—Ź –Ĺ–į ¬ę–Ľ–ĺ–ļ–į–Ľ—Ć–Ĺ–ĺ–Ķ¬Ľ —É–ľ–Ķ–Ĺ—Ć—ą–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –Ņ—É—ā–Ķ–ľ ¬ę—É–Ņ–ĺ—Ä—Ź–ī–ĺ—á–Ķ–Ĺ–Ĺ—č—Ö¬Ľ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–ĺ–≤, –Ņ—Ä–ĺ–ł—Ā—Ö–ĺ–ī–ł—ā —Ā—É–ľ–ľ–į—Ä–Ĺ–ĺ–Ķ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł –í—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ, –į –∂–ł–≤—č–Ķ –ĺ—Ä–≥–į–Ĺ–ł–∑–ľ—č —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤ –Ĺ–Ķ–ļ–ĺ—ā–ĺ—Ä–ĺ–ľ —Ä–ĺ–ī–Ķ –ļ–į—ā–į–Ľ–ł–∑–į—ā–ĺ—Ä–į–ľ–ł —ć—ā–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ü–Ķ—Ā—Ā–į. –Ę–į–ļ–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ, –Ĺ–į–Ī–Ľ—é–ī–į–Ķ—ā—Ā—Ź –≤—č–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –≤—ā–ĺ—Ä–ĺ–≥–ĺ –∑–į–ļ–ĺ–Ĺ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –Ĺ–Ķ—ā –Ĺ–ł–ļ–į–ļ–ĺ–≥–ĺ –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–į –≤–ĺ–∑–Ĺ–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ł—Ź –ł —Ā—É—Č–Ķ—Ā—ā–≤–ĺ–≤–į–Ĺ–ł—Ź –∂–ł–≤—č—Ö –ĺ—Ä–≥–į–Ĺ–ł–∑–ľ–ĺ–≤ –≤–ĺ–Ņ—Ä–Ķ–ļ–ł –≥–Ľ–ĺ–Ī–į–Ľ—Ć–Ĺ–ĺ–Ļ —ā–Ķ–Ĺ–ī–Ķ–Ĺ—Ü–ł–ł –≤—Ā–Ķ–Ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ –ļ —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł—é ¬ę–Ī–Ķ—Ā–Ņ–ĺ—Ä—Ź–ī–ļ–į¬Ľ.
–ě –Ĺ–į—É—á–Ĺ–ĺ‚Äď–ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ź—Ö –Ņ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ –≤ –°–°–°–†
–í –ļ–ĺ–Ĺ—Ü–Ķ 30-—Ö –ł –≤ –Ņ–ĺ—Ā–Ľ–Ķ–ī—É—é—Č–ł–Ķ –≥–ĺ–ī—č –≤–ĺ–∑—Ä–ĺ—Ā–Ľ–į —Ä–ĺ–Ľ—Ć –ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ä–į–Ī–ĺ—ā—č –Ĺ–į–ī –ļ—É—Ä—Ā–ĺ–ľ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –ü—Ä–ł —ć—ā–ĺ–ľ –≤–ĺ–∑—Ä–ĺ—Ā –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā –ļ –Ņ–ĺ—Ā—ā–į–Ĺ–ĺ–≤–ļ–Ķ –ł –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź–ľ –ľ–Ĺ–ĺ–≥–ł—Ö –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, —á—ā–ĺ –Ņ—Ä–ł–≤–Ķ–Ľ–ĺ –ļ –ĺ—Ä–≥–į–Ĺ–ł–∑–į—Ü–ł–ł –ł –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł—é —Ä—Ź–ī–į –ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–Ļ —Ā —ą–ł—Ä–ĺ–ļ–ł–ľ –Ņ—Ä–ł–≤–Ľ–Ķ—á–Ķ–Ĺ–ł–Ķ–ľ –Ņ—Ä–ĺ—Ą–Ķ—Ā—Ā–ĺ—Ä–ĺ–≤, –Ņ—Ä–Ķ–Ņ–ĺ–ī–į–≤–į—ā–Ķ–Ľ–Ķ–Ļ –ł —Ā–Ņ–Ķ—Ü–ł–į–Ľ–ł—Ā—ā–ĺ–≤ –≤ –ĺ–Ī–Ľ–į—Ā—ā–ł —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. –ü–Ķ—Ä–≤—č–Ķ —ā–į–ļ–ł–Ķ –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–ł –Ī—č–Ľ–ł –ĺ—Ä–≥–į–Ĺ–ł–∑–ĺ–≤–į–Ĺ—č –≤ –ļ–ĺ–Ĺ—Ü–Ķ —ā—Ä–ł–ī—Ü–į—ā—č—Ö –≥–ĺ–ī–ĺ–≤. –ě—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ —Ä–į—Ā—ą–ł—Ä–Ķ–Ĺ–Ĺ–ĺ–Ļ –Ņ–ĺ —Ā–ĺ—Ā—ā–į–≤—É –ł —á–ł—Ā–Ľ—É –ī–ĺ–ļ–Ľ–į–ī–ĺ–≤ –Ī—č–Ľ–į –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ź, –Ņ—Ä–ĺ–≤–Ķ–ī—Ď–Ĺ–Ĺ–į—Ź –≤ 1939 –≥–ĺ–ī—É –Ņ–ĺ–ī –Ņ—Ä–Ķ–ī—Ā–Ķ–ī–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ–ľ –į–ļ–į–ī–Ķ–ľ–ł–ļ–į –ú. –í. –ö–ł—Ä–Ņ–ł—á—Ď–≤–į. –°–Ľ–Ķ–ī—É—é—Č–ł–Ķ –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–ł, –Ĺ–į–ľ–Ķ—á–Ķ–Ĺ–Ĺ—č–Ķ –Ĺ–į 1940 –ł 1941 –≥–ĺ–ī—č –Ĺ–Ķ —Ā–ĺ—Ā—ā–ĺ—Ź–Ľ–ł—Ā—Ć, –ł –≤–ĺ–∑–ĺ–Ī–Ĺ–ĺ–≤–ł–Ľ–ł—Ā—Ć –Ņ–ĺ—Ā–Ľ–Ķ –ĺ–ļ–ĺ–Ĺ—á–į–Ĺ–ł–ł –≤–ĺ–Ļ–Ĺ—č ‚ÄĒ –≤ –ļ–ĺ–Ĺ—Ü–Ķ —Ā–ĺ—Ä–ĺ–ļ–ĺ–≤—č—Ö –ł –≤ –Ĺ–į—á–į–Ľ–Ķ 50—Ö –≥–ĺ–ī–ĺ–≤.
–í 1962 –≥. —Ā–ĺ—Ā—ā–ĺ—Ź–Ľ–ł—Ā—Ć –ī–≤–Ķ –Ĺ–į—É—á–Ĺ–ĺ-–ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ł–Ķ –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–ł –Ņ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ, –ĺ–ī–Ĺ–į –≤ –ú–ĺ—Ā–ļ–≤–Ķ, –ī—Ä—É–≥–į—Ź –≤ –ě–ī–Ķ—Ā—Ā–Ķ. –Ě–į–ł–Ī–ĺ–Ľ—Ć—ą–ł–Ļ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–Ľ–į –ľ–ĺ—Ā–ļ–ĺ–≤—Ā–ļ–į—Ź –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ź, –Ņ–ĺ–ī –Ņ—Ä–Ķ–ī—Ā–Ķ–ī–į—ā–Ķ–Ľ—Ć—Ā—ā–≤–ĺ–ľ –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź, –≤ –ļ–ĺ—ā–ĺ—Ä–ĺ–Ļ, –Ī—č–Ľ–ł –∑–į—Ā–Ľ—É—ą–į–Ĺ—č –ī–ĺ–ļ–Ľ–į–ī—č –Ņ–ĺ —ā—Ä—Ď–ľ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į–ľ: –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—č –ł –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ—Ā—ā–ł —Ä–į—Ā—á—Ď—ā–Ĺ—č—Ö –Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ļ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł; –≤–∑–į–ł–ľ–ĺ–ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł; —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –ł —ć–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–į–Ľ—Ć–Ĺ—č–Ķ –ł—Ā—Ā–Ľ–Ķ–ī–ĺ–≤–į–Ĺ–ł—Ź –≤–Ķ—Č–Ķ—Ā—ā–≤–į. –ü–Ķ—Ä–≤–ĺ–Ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–Ķ –Ī—č–Ľ–ł –Ņ–ĺ—Ā–≤—Ź—Č–Ķ–Ĺ—č –ī–ĺ–ļ–Ľ–į–ī—č: –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź: –ü–ĺ—Ā—ā—É–Ľ–į—ā—č, —Ā—Ö–Ķ–ľ—č –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ł—Ź –ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ –≤—č—Ä–į–∂–Ķ–Ĺ–ł—Ź –ĺ—Ā–Ĺ–ĺ–≤–Ĺ—č—Ö –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ĺ–≤ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –ź. –ź. –ď—É—Ö–ľ–į–Ĺ–į: –ě —Ä–į–∑–Ľ–ł—á–Ĺ—č—Ö —Ā–ł—Ā—ā–Ķ–ľ–į—Ö –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź –≤—ā–ĺ—Ä–ĺ–≥–ĺ –Ĺ–į—á–į–Ľ–į —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, –ė. –ü. –Ď–į–∑–į—Ä–ĺ–≤–į: –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į —Ā–ł—Ā—ā–Ķ–ľ –Ņ—Ä–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č—Ö –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ—č—Ö —ā–Ķ–ľ–Ņ–Ķ—Ä–į—ā—É—Ä–į—Ö –ł –ī—Ä. –ě—Ā–ĺ–Ī–Ķ–Ĺ–Ĺ–ĺ –ĺ–∂–ł–≤–Ľ—Ď–Ĺ–Ĺ—č–ľ–ł –ł –ľ–Ĺ–ĺ–≥–ĺ—á–ł—Ā–Ľ–Ķ–Ĺ–Ĺ—č–ľ–ł –Ī—č–Ľ–ł –≤—č—Ā—ā—É–Ņ–Ľ–Ķ–Ĺ–ł—Ź –Ņ–ĺ –Ņ–Ķ—Ä–≤–ĺ–Ļ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–Ķ, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł, –Ņ–ĺ –ī–ĺ–ļ–Ľ–į–ī—É –Ě. –ė. –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ź. –ö —Ā–ĺ–∂–į–Ľ–Ķ–Ĺ–ł—é, –Ņ–ĺ —Ā–Ľ–ĺ–≤–į–ľ –ź. –°. –Į—Ā—ā—Ä–∂–Ķ–ľ–Ī—Ā–ļ–ĺ–≥–ĺ, –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł—Ź –Ĺ–Ķ —Ā–ľ–ĺ–≥–Ľ–į –Ņ–ĺ —ć—ā–ł–ľ –ī–ĺ–ļ–Ľ–į–ī–į–ľ –Ņ—Ä–ł–Ļ—ā–ł –ļ –ļ–į–ļ–ł–ľ-–Ľ–ł–Ī–ĺ –≤—č–≤–ĺ–ī–į–ľ –ł —Ä–Ķ–ļ–ĺ–ľ–Ķ–Ĺ–ī–į—Ü–ł—Ź–ľ. [53].
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
- ‚ÜĎ 1 2 –•–ł–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, —ā.1, 1988, —Ā. 432.
- ‚ÜĎ –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 2010, —Ā. 49.
- ‚ÜĎ 1 2 –Ď–°–≠, 3-–Ķ –ł–∑–ī., —ā.5, 1971, —Ā. 495.
- ‚ÜĎ 1 2 –§–ł–∑–ł–ļ–į. –Ď–ĺ–Ľ—Ć—ą–ĺ–Ļ —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–Ľ–ĺ–≤–į—Ä—Ć, 1998, —Ā. 95.
- ‚ÜĎ –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 1934, —Ā. 156.
- ‚ÜĎ 1 2 –†—č–Ĺ–ī–ł–Ĺ –í. –í., –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –Ķ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ, 2002, —Ā. 37.
- ‚ÜĎ 1 2 –°–ł–≤—É—Ö–ł–Ĺ –Ē. –í., –ě–Ī—Č–ł–Ļ –ļ—É—Ä—Ā —Ą–ł–∑–ł–ļ–ł —ā.2, 2005, —Ā. 85.
- ‚ÜĎ –†—č–Ĺ–ī–ł–Ĺ –í. –í., –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –Ķ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ, 2002, —Ā. 62.
- ‚ÜĎ –í—É–ļ–į–Ľ–ĺ–≤–ł—á –ú. –ü.,–Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1968, —Ā. 94‚ÄĒ95.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 130.
- ‚ÜĎ –†—č–Ĺ–ī–ł–Ĺ –í. –í., –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –Ķ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ, 2002, —Ā. 11.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 131.
- ‚ÜĎ 1 2 3 –ö–ł—Ä–ł–Ľ–Ľ–ł–Ĺ –í. –ź. –ł –ī—Ä., –Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1983, —Ā. 49.
- ‚ÜĎ –ö–ł—Ä–ł–Ľ–Ľ–ł–Ĺ –í. –ź. –ł –ī—Ä., –Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1983, —Ā. 50.
- ‚ÜĎ –Ď–†–≠, —ā.6, 2006, —Ā. 80‚ÄĒ81.
- ‚ÜĎ –Ď—Ä–ĺ–ī—Ź–Ĺ—Ā–ļ–ł–Ļ –í. –ú., –í–Ķ—á–Ĺ—č–Ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć –Ņ—Ä–Ķ–∂–ī–Ķ –ł —ā–Ķ–Ņ–Ķ—Ä—Ć, 1989, —Ā. 114.
- ‚ÜĎ –°–ł–≤—É—Ö–ł–Ĺ –Ē. –í., –ě–Ī—Č–ł–Ļ –ļ—É—Ä—Ā —Ą–ł–∑–ł–ļ–ł —ā.2, 2005, —Ā. 90.
- ‚ÜĎ –†—č–Ĺ–ī–ł–Ĺ –í. –í., –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –Ķ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ, 2002, —Ā. 22.
- ‚ÜĎ –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 2010, —Ā. 58.
- ‚ÜĎ –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 2010, —Ā. 75.
- ‚ÜĎ –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ –õ., –ė–∑–Ī—Ä–į–Ĺ–Ĺ—č–Ķ —ā—Ä—É–ī—č, 1984, —Ā. 190‚ÄĒ235.
- ‚ÜĎ –•–į–Ļ—ā—É–Ĺ –°. –Ē., –ö—Ä–ł–∑–ł—Ā –Ĺ–į—É–ļ–ł –ļ–į–ļ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ļ—Ä–ł–∑–ł—Ā–į —ā–Ķ–ĺ—Ä–ł–ł –Ņ–ĺ–∑–Ĺ–į–Ĺ–ł—Ź: –ļ—Ä–ł–∑–ł—Ā —ā–Ķ–ĺ—Ä–ł–ł –Ņ–ĺ–∑–Ĺ–į–Ĺ–ł—Ź, 2014, —Ā. 142‚ÄĒ144.
- ‚ÜĎ –®–į–ľ–Ī–į–ī–į–Ľ—Ć –ü., –†–į–∑–≤–ł—ā–ł–Ķ –ł –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł, 1967, —Ā. 61‚ÄĒ66.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 197‚ÄĒ198.
- ‚ÜĎ –ď–Ķ–Ľ—Ć—Ą–Ķ—Ä –Į. –ú., –ė—Ā—ā–ĺ—Ä–ł—Ź –ł –ľ–Ķ—ā–ĺ–ī–ĺ–Ľ–ĺ–≥–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł, 1981, —Ā. 207‚ÄĒ208.
- ‚ÜĎ –ď–Ķ–Ľ—Ć—Ą–Ķ—Ä –Į. –ú., –ė—Ā—ā–ĺ—Ä–ł—Ź –ł –ľ–Ķ—ā–ĺ–ī–ĺ–Ľ–ĺ–≥–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł, 1981, —Ā. 207‚ÄĒ208.
- ‚ÜĎ 1 2 –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 223.
- ‚ÜĎ –ď—É—Ö–ľ–į–Ĺ –ź. –ź., –ě–Ī –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 2010, —Ā. 226‚ÄĒ227.
- ‚ÜĎ –ď–Ķ–Ľ—Ć—Ą–Ķ—Ä –Į. –ú., –ė—Ā—ā–ĺ—Ä–ł—Ź –ł –ľ–Ķ—ā–ĺ–ī–ĺ–Ľ–ĺ–≥–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł, 1981, —Ā. 208.
- ‚ÜĎ –†–į–∑–≤–ł—ā–ł–Ķ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł, 1964, —Ā. 197.
- ‚ÜĎ –ď—É—Ö–ľ–į–Ĺ –ź. –ź., –ě–Ī –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 2010, —Ā. 370.
- ‚ÜĎ –ď—É—Ö–ľ–į–Ĺ –ź. –ź., –ě–Ī –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 2010, —Ā. 366.
- ‚ÜĎ –†–į–∑–≤–ł—ā–ł–Ķ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł, 1964, —Ā. 269‚ÄĒ270).
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 241‚ÄĒ242.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 244.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 245‚ÄĒ246.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—č —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 1968, —Ā. 55.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—č —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 1968, —Ā. 55‚ÄĒ56.
- ‚ÜĎ –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1954, —Ā. 166‚ÄĒ184.
- ‚ÜĎ –Ę–Ķ–∑–ł—Ā—č –ī–ĺ–ļ–Ľ–į–ī–ĺ–≤ –Ĺ–į –Ņ–Ķ—Ä–≤–ĺ–Ļ –Ĺ–į—É—á–Ĺ–ĺ-–ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–ł –Ņ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ, 1962, —Ā. 9‚ÄĒ10.
- ‚ÜĎ –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 2010, —Ā. 136‚ÄĒ137.
- ‚ÜĎ –†—Ė–∑–į–ļ –í., –†—Ė–∑–į–ļ –Ü., –†—É–ī–į–≤—Ā—Ć–ļ–ł–Ļ –ē., –ö—Ä—Ė–ĺ–≥–Ķ–Ĺ–Ĺ–į —Ą—Ė–∑–ł–ļ–į —Ė —ā–Ķ—Ö–Ĺ—Ė–ļ–į, 2006, —Ā. 18‚ÄĒ19.
- ‚ÜĎ –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 2010, —Ā. 138.
- ‚ÜĎ 1 2 –Ę–Ķ–∑–ł—Ā—č –ī–ĺ–ļ–Ľ–į–ī–ĺ–≤ –Ĺ–į –Ņ–Ķ—Ä–≤–ĺ–Ļ –Ĺ–į—É—á–Ĺ–ĺ-–ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–ł –Ņ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ, 1962, —Ā. 16.
- ‚ÜĎ –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 2010, —Ā. 141‚ÄĒ143.
- ‚ÜĎ –í—É–ļ–į–Ľ–ĺ–≤–ł—á –ú. –ü.,–Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 1968, —Ā. 96‚ÄĒ97.
- ‚ÜĎ –ď—É—Ö–ľ–į–Ĺ –ź. –ź., –ě–Ī –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 2010, —Ā. 351.
- ‚ÜĎ –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–į-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā –Ę. –ź., –Ě–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā—Ć,–ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –ł –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 1928, —Ā. 3.
- ‚ÜĎ –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–į-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā –Ę. –ź., –Ě–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā—Ć,–ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –ł –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł, 1928, —Ā. 26‚ÄĒ27.
- ‚ÜĎ –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į, 2010, —Ā. 82‚ĒÄ84.
- ‚ÜĎ John Rennie 15 Answers to Creationist Nonsense.
- ‚ÜĎ –ú–į—Ä–ļ–ĺ–≤ –ź., –†–ĺ–∂–ī–Ķ–Ĺ–ł–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł. –≠–≤–ĺ–Ľ—é—Ü–ł–ĺ–Ĺ–Ĺ–į—Ź –Ī–ł–ĺ–Ľ–ĺ–≥–ł—Ź —Ā–Ķ–≥–ĺ–ī–Ĺ—Ź: –Ĺ–Ķ–ĺ–∂–ł–ī–į–Ĺ–Ĺ—č–Ķ –ĺ—ā–ļ—Ä—č—ā–ł—Ź –ł –Ĺ–ĺ–≤—č–Ķ –≤–ĺ–Ņ—Ä–ĺ—Ā—č, 2010, —Ā. 199.
- ‚ÜĎ –Į—Ā—ā—Ä–∂–Ķ–ľ–Ī—Ā–ļ–ł–Ļ –ź. –°., –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į –ł –ł—Ā—ā–ĺ—Ä–ł—Ź –Ķ—Ď —Ä–į–∑–≤–ł—ā–ł—Ź, 1966, —Ā. 306.
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
- –ź—Ą–į–Ĺ–į—Ā—Ć–Ķ–≤–į-–≠—Ä–Ķ–Ĺ—Ą–Ķ—Ā—ā –Ę. –ź. –Ě–Ķ–ĺ–Ī—Ä–į—ā–ł–ľ–ĺ—Ā—ā—Ć, –ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ĺ—Ā—ā—Ć –ł –≤—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł (—Ä—É—Ā.) // –Ė—É—Ä–Ĺ–į–Ľ –Ņ—Ä–ł–ļ–Ľ–į–ī–Ĺ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł. ‚ÄĒ 1928. ‚ÄĒ –Ę. 5, ‚ĄĖ 3‚ÄĒ4. ‚ÄĒ –°. 3‚ÄĒ30.
- –Ď–į–∑–į—Ä–ĺ–≤ –ė. –ü. –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į. ‚ÄĒ 5-–Ķ –ł–∑–ī. ‚ÄĒ –°–ü–Ī.‚ÄĒ–ú.‚ÄĒ–ö—Ä–į—Ā–Ĺ–ĺ–ī–į—Ä: –õ–į–Ĺ—Ć, 2010. ‚ÄĒ 384 —Ā. ‚ÄĒ (–£—á–Ķ–Ī–Ĺ–ł–ļ–ł –ī–Ľ—Ź –≤—É–∑–ĺ–≤. –°–Ņ–Ķ—Ü–ł–į–Ľ—Ć–Ĺ–į—Ź –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–į). ‚ÄĒ ISBN 978-5-8114-1003-3.
- –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė. –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į. ‚ÄĒ –ú.: –ď–ĺ—Ā—ć–Ĺ–Ķ—Ä–≥–ĺ–ł–∑–ī–į—ā, 1954. ‚ÄĒ 416 —Ā.
- –Ď–Ķ–Ľ–ĺ–ļ–ĺ–Ĺ—Ć –Ě. –ė. –ě—Ā–Ĺ–ĺ–≤–Ĺ—č–Ķ –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ—č —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. ‚ÄĒ –ú.: –Ě–Ķ–ī—Ä–į, 1968. ‚ÄĒ 112 —Ā.
- –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ –õ. –ė–∑–Ī—Ä–į–Ĺ–Ĺ—č–Ķ —ā—Ä—É–ī—č / –ě—ā–≤. —Ä–Ķ–ī. –õ. –°. –ü–ĺ–Ľ–į–ļ. ‚ÄĒ –ú.: –Ě–į—É–ļ–į, 1984. ‚ÄĒ 590 —Ā. ‚ÄĒ (–ö–Ľ–į—Ā—Ā–ł–ļ–ł –Ĺ–į—É–ļ–ł).
- –Ď–ĺ–Ľ—Ć—ą–į—Ź –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź –≠–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź / –ď–Ľ. —Ä–Ķ–ī. –ź. –ú. –ü—Ä–ĺ—Ö–ĺ—Ä–ĺ–≤. ‚ÄĒ 3-–Ķ –ł–∑–ī.. ‚ÄĒ –ú.: –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź –≠–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, 1971. ‚ÄĒ –Ę. 5: –í–Ķ—ą–ł–Ĺ ‚ÄĒ –ď–į–∑–Ľ–ł. ‚ÄĒ 640 —Ā. –ź—Ä—Ö–ł–≤–Ĺ–į—Ź –ļ–ĺ–Ņ–ł—Ź –ĺ—ā 6 —Ā–Ķ–Ĺ—ā—Ź–Ī—Ä—Ź 2018 –Ĺ–į Wayback Machine
- –Ď–ĺ–Ľ—Ć—ą–į—Ź —Ä–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź. ‚ÄĒ –ú.: –Ď–ĺ–Ľ—Ć—ą–į—Ź –†–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, 2006. ‚ÄĒ –Ę. 6: –í–ĺ—Ā—Ć–ľ–Ķ—Ä–ł—á–Ĺ—č–Ļ –Ņ—É—ā—Ć ‚ÄĒ –ď–Ķ—Ä–ľ–į–Ĺ—Ü—č. ‚ÄĒ 768 —Ā. ‚ÄĒ ISBN 5-85270-335-4.
- –Ď—Ä–ĺ–ī—Ź–Ĺ—Ā–ļ–ł–Ļ –í. –ú. –í–Ķ—á–Ĺ—č–Ļ –ī–≤–ł–≥–į—ā–Ķ–Ľ—Ć ‚ÄĒ –Ņ—Ä–Ķ–∂–ī–Ķ –ł —ā–Ķ–Ņ–Ķ—Ä—Ć. –ě—ā —É—ā–ĺ–Ņ–ł–ł ‚ÄĒ –ļ –Ĺ–į—É–ļ–Ķ, –ĺ—ā –Ĺ–į—É–ļ–ł ‚ÄĒ –ļ —É—ā–ĺ–Ņ–ł–ł. ‚ÄĒ –ú.: –≠–Ĺ–Ķ—Ä–≥–ĺ–į—ā–ĺ–ľ–ł–∑–ī–į—ā, 1989. ‚ÄĒ 256 —Ā. ‚ÄĒ (–Ě–į—É—á–Ĺ–ĺ-–Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ–į—Ź –Ī–ł–Ī–Ľ–ł–ĺ—ā–Ķ–ļ–į —ą–ļ–ĺ–Ľ—Ć–Ĺ–ł–ļ–į). ‚ÄĒ ISBN 5-283-00058-3.
- –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł: –°–į–ī–ł –ö–į—Ä–Ĺ–ĺ ‚ÄĒ –í. –Ę–ĺ–ľ—Ā–ĺ–Ĺ-–ö–Ķ–Ľ—Ć–≤–ł–Ĺ ‚ÄĒ –†. –ö–Ľ–į—É–∑–ł—É—Ā ‚ÄĒ –õ. –Ď–ĺ–Ľ—Ć—Ü–ľ–į–Ĺ ‚ÄĒ –ú. –°–ľ–ĺ–Ľ—É—Ö–ĺ–≤—Ā–ļ–ł–Ļ / –ü–ĺ–ī. —Ä–Ķ–ī. –ł —Ā –Ņ—Ä–Ķ–ī. –ź. –ö. –Ę–ł–ľ–ł—Ä—Ź–∑–Ķ–≤–į. ‚ÄĒ –ú.‚ÄĒ–õ.: –ď–ĺ—Ā—ā–Ķ—Ö–ł–∑–ī–į—ā, 1934. ‚ÄĒ 311 —Ā.
- –í—É–ļ–į–Ľ–ĺ–≤–ł—á –ú. –ü. –Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į. ‚ÄĒ –ú.: –≠–Ĺ–Ķ—Ä–≥–ł—Ź, 1968. ‚ÄĒ 496 —Ā.
- –ď–Ķ–Ľ—Ć—Ą–Ķ—Ä –Į. –ú. –ė—Ā—ā–ĺ—Ä–ł—Ź –ł –ľ–Ķ—ā–ĺ–ī–ĺ–Ľ–ĺ–≥–ł—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł —Ā—ā–į—ā–ł—Ā—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł. ‚ÄĒ 2-–Ķ –ł–∑–ī., –Ņ–Ķ—Ä–Ķ—Ä–į–Ī. –ł –ī–ĺ–Ņ. ‚ÄĒ –ú.: –í—č—Ā—ą–į—Ź —ą–ļ–ĺ–Ľ–į, 1981. ‚ÄĒ 536 —Ā.
- –ď—É—Ö–ľ–į–Ĺ –ź. –ź. –ě–Ī –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź—Ö —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł. ‚ÄĒ 2-–Ķ –ł–∑–ī. ‚ÄĒ –ú.: –õ–ö–ė, 2010. ‚ÄĒ 384 —Ā. ‚ÄĒ ISBN 978-5-382-01105-9.
- –ö–ł—Ä–ł–Ľ–Ľ–ł–Ĺ –í. –ź. –ł –ī—Ä. –Ę–Ķ—Ö–Ĺ–ł—á–Ķ—Ā–ļ–į—Ź —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į. ‚ÄĒ 4-–Ķ –ł–∑–ī.. ‚ÄĒ –ú.: –≠–Ĺ–Ķ—Ä–≥–ĺ–į—ā–ĺ–ľ–ł–∑–ī–į—ā, 1983. ‚ÄĒ 416 —Ā.
- –ú–į—Ä–ļ–ĺ–≤ –ź. –†–ĺ–∂–ī–Ķ–Ĺ–ł–Ķ —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł. –≠–≤–ĺ–Ľ—é—Ü–ł–ĺ–Ĺ–Ĺ–į—Ź –Ī–ł–ĺ–Ľ–ĺ–≥–ł—Ź —Ā–Ķ–≥–ĺ–ī–Ĺ—Ź: –Ĺ–Ķ–ĺ–∂–ł–ī–į–Ĺ–Ĺ—č–Ķ –ĺ—ā–ļ—Ä—č—ā–ł—Ź –ł –Ĺ–ĺ–≤—č–Ķ –≤–ĺ–Ņ—Ä–ĺ—Ā—č. ‚ÄĒ –ú.: –ź—Ā—ā—Ä–Ķ–Ľ—Ć, 2010. ‚ÄĒ 527 —Ā. ‚ÄĒ ISBN 978-5-271-24663-0.
- –†–į–∑–≤–ł—ā–ł–Ķ —Ā–ĺ–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ą–ł–∑–ł–ļ–ł / –ě—ā–≤. —Ä–Ķ–ī. –ö—É–∑–Ĺ–Ķ—Ü–ĺ–≤ –Ď. –ď.. ‚ÄĒ –ú.: –Ě–į—É–ļ–į, 1964. ‚ÄĒ 331 —Ā.
- –†—Ė–∑–į–ļ –í., –†—Ė–∑–į–ļ –Ü., –†—É–ī–į–≤—Ā—Ć–ļ–ł–Ļ –ē. –ö—Ä—Ė–ĺ–≥–Ķ–Ĺ–Ĺ–į —Ą—Ė–∑–ł–ļ–į —Ė —ā–Ķ—Ö–Ĺ—Ė–ļ–į. ‚ÄĒ –ö–ł–Ķ–≤: –Ě–į—É–ļ–ĺ–≤–į –ī—É–ľ–ļ–į, 2006. ‚ÄĒ 512 —Ā. ‚ÄĒ ISBN 966-00-480-X..
- –†—č–Ĺ–ī–ł–Ĺ –í. –í. –í—ā–ĺ—Ä–ĺ–Ķ –Ĺ–į—á–į–Ľ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–ł –ł –Ķ–≥–ĺ —Ä–į–∑–≤–ł—ā–ł–Ķ. ‚ÄĒ –≥. –ü–į–≤–Ľ–ĺ–ī–į—Ä: –ü–ď–£, 2002. ‚ÄĒ 459 —Ā. ‚ÄĒ ISBN ISBN 9965-568-70-2.
- –°–ł–≤—É—Ö–ł–Ĺ –Ē. –í. –ě–Ī—Č–ł–Ļ –ļ—É—Ä—Ā —Ą–ł–∑–ł–ļ–ł. ‚ÄĒ 5-–Ķ –ł–∑–ī. ‚ÄĒ –ú.: –§–ł–∑–ľ–į—ā–Ľ–ł—ā, 2005. ‚ÄĒ –Ę. 2. ‚ÄĒ 544 —Ā. ‚ÄĒ ISBN 5-9221-0601-5.
- –Ę–Ķ–∑–ł—Ā—č –ī–ĺ–ļ–Ľ–į–ī–ĺ–≤ –Ĺ–į –Ņ–Ķ—Ä–≤–ĺ–Ļ –Ĺ–į—É—á–Ĺ–ĺ- –ľ–Ķ—ā–ĺ–ī–ł—á–Ķ—Ā–ļ–ĺ–Ļ –ļ–ĺ–Ĺ—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–ł –Ņ–ĺ —ā–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–Ķ. ‚ÄĒ –ú.: –ď–ĺ—Ā—ā–ĺ–Ņ—ā–Ķ—Ö–ł–∑–ī–į—ā, 1962. ‚ÄĒ 80 —Ā.
- –§–ł–∑–ł–ļ–į. –Ď–ĺ–Ľ—Ć—ą–ĺ–Ļ —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—á–Ķ—Ā–ļ–ł–Ļ —Ā–Ľ–ĺ–≤–į—Ä—Ć / –ď–Ľ. —Ä–Ķ–ī. –ź. –ú. –ü—Ä–ĺ—Ö–ĺ—Ä–ĺ–≤. ‚ÄĒ –ú.: –Ď–ĺ–Ľ—Ć—ą–į—Ź –†–ĺ—Ā—Ā–ł–Ļ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, 1998. ‚ÄĒ 944 —Ā. ‚ÄĒ ISBN 5-85270-306-0.
- –•–į–Ļ—ā—É–Ĺ –°. –Ē. –ö—Ä–ł–∑–ł—Ā –Ĺ–į—É–ļ–ł –ļ–į–ļ –∑–Ķ—Ä–ļ–į–Ľ—Ć–Ĺ–ĺ–Ķ –ĺ—ā—Ä–į–∂–Ķ–Ĺ–ł–Ķ –ļ—Ä–ł–∑–ł—Ā–į —ā–Ķ–ĺ—Ä–ł–ł –Ņ–ĺ–∑–Ĺ–į–Ĺ–ł—Ź: –ļ—Ä–ł–∑–ł—Ā —ā–Ķ–ĺ—Ä–ł–ł –Ņ–ĺ–∑–Ĺ–į–Ĺ–ł—Ź. ‚ÄĒ –ú.: –õ–Ķ–Ĺ–į–Ĺ–ī, 2014. ‚ÄĒ 448 —Ā. ‚ÄĒ ISBN 978-5-9710=1296-2.
- –•–ł–ľ–ł—á–Ķ—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź / –ď–Ľ. —Ä–Ķ–ī. –ė. –õ. –ö–Ĺ—É–Ĺ—Ź–Ĺ—Ü. ‚ÄĒ –ú.: –°–ĺ–≤–Ķ—ā—Ā–ļ–į—Ź —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł—Ź, 1988. ‚ÄĒ –Ę. 1: –ź–Ī–Ľ ‚ÄĒ –Ē–į—Ä. ‚ÄĒ 624 —Ā.
- –®–į–ľ–Ī–į–ī–į–Ľ—Ć –ü. –†–į–∑–≤–ł—ā–ł–Ķ –ł –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź —ć–Ĺ—ā—Ä–ĺ–Ņ–ł–ł. ‚ÄĒ –ú.: –Ě–į—É–ļ–į, 1967. ‚ÄĒ 280 —Ā.
- –Į—Ā—ā—Ä–∂–Ķ–ľ–Ī—Ā–ļ–ł–Ļ –ź. –°. –Ę–Ķ—Ä–ľ–ĺ–ī–ł–Ĺ–į–ľ–ł–ļ–į –ł –ł—Ā—ā–ĺ—Ä–ł—Ź –Ķ—Ď —Ä–į–∑–≤–ł—ā–ł—Ź. ‚ÄĒ –ú.‚ÄĒ–õ.: –≠–Ĺ–Ķ—Ä–≥–ł—Ź, 1966. ‚ÄĒ 668 —Ā.
- John Rennie,. 15 Answers to Creationist Nonsense (–į–Ĺ–≥–Ľ.). ‚ÄĒ USA.