Вещественная проективная плоскость
|
Read other articles:

NewJeans discographyNewJeans in 2022EPs2Singles8Single albums1Remix albums1Promotional singles5 South Korean girl group NewJeans has released two extended plays, one single album, eight singles, and three promotional singles. The group's first release, their self-titled extended play (2022), topped the South Korean Circle Album Chart and became the best-selling debut album by a K-pop female act, with over one million copies sold.[1] It was supported by three singles: Attention, Hype ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

Часть серии статей о Холокосте Идеология и политика Расовая гигиена · Расовый антисемитизм · Нацистская расовая политика · Нюрнбергские расовые законы Шоа Лагеря смерти Белжец · Дахау · Майданек · Малый Тростенец · Маутхаузен ·&...

Glam punkThe New York Dolls, tampil di festival Burlington Sound of Music pada 2010Nama lainMock rockSumber aliranGlam rockproto-punkSumber kebudayaanAwal 1970an, New York CityBentuk turunan Punk rock new wave Topik lainnya Androgyny new romanticism Oi! post-punk gothic rock glam metal Glam punk (kadang-kadang disebut mock rock) adalah istilah yang digunakan secara retrospektif untuk menggambarkan tren berumur pendek untuk band-band yang menghasilkan bentuk proto-punk yang memasukkan unsur-un...

CO34Stasiun Sasago笹子駅Stasiun Sasago pada April 2018Lokasi1340, Sasago-machi Kuronoda, Ōtsuki-shi, Yamanashi-kenJepangKoordinat35°36′15″N 138°49′37″E / 35.604153°N 138.827047°E / 35.604153; 138.827047Koordinat: 35°36′15″N 138°49′37″E / 35.604153°N 138.827047°E / 35.604153; 138.827047Operator JR EastJalur■ Jalur Utama ChūōLetak100.4 km dari TokyoJumlah peron1 peron pulauJumlah jalur2Informasi lainStatusTanpa staf...

Gempa bumi Galilee 1837Waktu setempat16:00Lama20 detikKekuatan6.5 Mw[1]Episentrum33°00′N 35°30′E / 33.0°N 35.5°E / 33.0; 35.5Koordinat: 33°00′N 35°30′E / 33.0°N 35.5°E / 33.0; 35.5Wilayah bencanaSuriah, Palestina, YordaniaIntensitas maks.X (Ekstrem)Korban6,000–7,000 tewas Gempa bumi Galilea 1837, juga sering disebut gempa Safed, adalah gempa bumi yang mengguncang kawasan Galilea pada tanggal 1 Januari 1837. Pada ma...

Ravindra NandaProf. Ravindra NandaBorn (1943-02-19) 19 February 1943 (age 81)Lyallpur, British IndiaNationality AmericanEducationMaster of Dental Surgery (1964), PhD (1970), Certificate in Orthodontics (1978) [1]Alma materKing George's Medical College Lucknow University, Katholieke Universities (Nijmegen, the Netherlands), University of Connecticut[1]Occupation(s)Professor and Head of the Department of Craniofacial Sciences, Chair Division of Orthodontics[1...

Former railway station in Yakumo, Hokkaido, Japan Washinosu Station鷲ノ巣駅The station in October 2008General informationLocationYakumo, Futami District, HokkaidoJapanOperated by JR HokkaidoLine(s)■ Hakodate Main LineDistance84.2 km from HakodatePlatforms2 side platformsTracks2Other informationStatusClosedStation codeH53HistoryOpened1 September 1944 (1944-09-01)Closed25 March 2016 (2016-03-25)LocationWashinosu StationLocation within Japan Washinosu Station ...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Apple cultivar 'Melrose' appleSpeciesMalus domesticaHybrid parentageJonathan x Red DeliciousOrigin USA, Ohio Melrose is a modern cultivar of domesticated apple which was developed by Freeman S. Howlett, William J. Eyssen and their team at the Ohio Agricultural Experiment Station in Ohio, United States,[1] and is regarded as the unofficial apple of that state.[2] This apple was released by the Ohio Agricultural Experiment Station in Wooster, Ohio[2] during Wo...

English clergyman and scholar (1849–1909) Old Court of Selwyn College, Cambridge, with the Hall on the right Richard Appleton MA (17 February 1849 – 1 March 1909) was an English scholar, clergyman of the Church of England, and the fourth Master of Selwyn College, Cambridge, 1907 – 1909. He was a fellow of Trinity College, Cambridge, and a parish priest before moving to Selwyn.[1] Early life Appleton was born in Liverpool, the son of another Revd Richard Appleton and grandson...
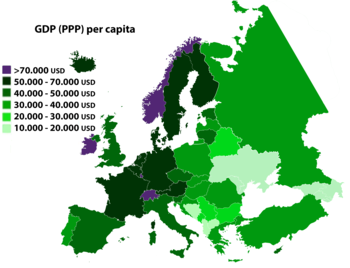
اقتصاد أوروباالإحصائياتالناتج الإجمالي $22.9 تريليون (إسمي)نمو الناتج الإجمالي 2.4% (2017)[2]نصيب الفرد من الناتج الإجمالي $27,330 (2017[1]البطالة 10.0% (نوفمبر 2009)تعديل - تعديل مصدري - تعديل ويكي بيانات جزء من سلسلة مقالات حولاقتصاد تاريخأفرع تاريخ الاقتصاد مدارس الاقتصاد اقتصاد ...

Skiing in unmarked or unpatrolled areas This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Backcountry skiing – news · newspapers · books · scholar · JSTOR (January 2011) (Learn how and when to remove this message) A set of backcountry ski runs in the Battle Range of the Canadian Rocky Mountains. Notice a minor...

Dave McCannMcCann circa 1909BornDavid McCann(1889-02-05)February 5, 1889Carleton Place, Ontario, CanadaDiedMarch 27, 1959(1959-03-27) (aged 70)Ottawa, Ontario, Canada[1]Occupation(s)CFL player, official, coach, Canadian Rugby Union President, Rules Committee Chairman David McCann (February 5, 1889 – March 27, 1959) was a Canadian Football League player, official, coach, and executive who was elected to the Canadian Football Hall of Fame in 1966. Biography Born in Ottawa, McCann...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (نوفمبر 2022) هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحس...

Babel routing protocol logo. The Babel routing protocol is a distance-vector routing protocol for Internet Protocol packet-switched networks that is designed to be robust and efficient on both wireless mesh networks and wired networks. Babel is described in RFC 8966.[1] Babel is based on the ideas in Destination-Sequenced Distance Vector routing (DSDV), Ad hoc On-Demand Distance Vector Routing (AODV), and Cisco's Enhanced Interior Gateway Routing Protocol (EIGRP), but uses different t...

This article contains dynamic lists that may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. Map of per capita police killings in the United States in 2018.[1] Below are lists of people killed by law enforcement in the United States, both on duty and off duty. Although Congress instructed the Attorney General in 1994 to compile and publish annual statistics on police use of excessive force, this was never car...

「花」のその他の用法については「花 (曖昧さ回避)」をご覧ください。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 花 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ ...

Ne doit pas être confondu avec Îlot de Langerhans ou cellule géante de type Langhans. Cellules de Langerhans dans l'épiderme Les cellules de Langerhans sont des macrophages résidents du système immunitaire présents la couche épithéliale [1]. Ils sont des présentateurs d'antigènes. On les retrouve dans le tissu cutané, entre les kératinocytes des couches basale et épineuse de l'épiderme et plus particulièrement dans la couche épineuse, les ganglions lymphatiques et quelques a...

Jim LovellAstronauta della NASANazionalità Stati Uniti StatusRitirato Data di nascita25 marzo 1928 Selezione17 settembre 1962(gruppo 2 NASA) Primo lancio4 dicembre 1965 Ultimo atterraggio17 aprile 1970 Altre attivitàPilota collaudatore Tempo nello spazio29 giorni, 19 ore e 3 minuti Missioni Gemini 7 Gemini 12 Apollo 8 Apollo 13 Data ritiromarzo 1973 Modifica dati su Wikidata · Manuale James Arthur Lovell Jr., detto Jim (Cleveland, 25 marzo 1928), è un astronauta statunitense del...













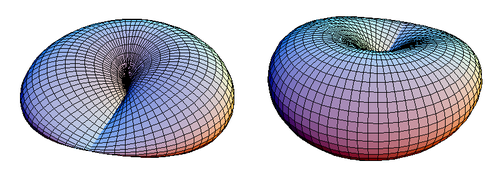
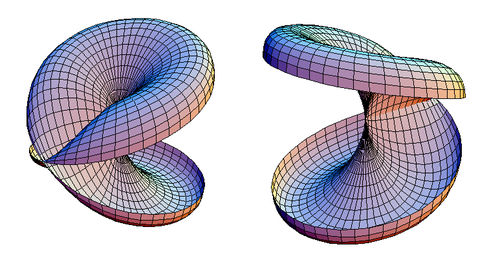
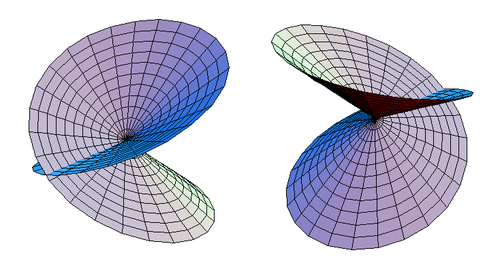





![{\displaystyle [x:y:z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/824605c6ea4c4537ff9daf4ce86c26ef6a30f529)
![{\displaystyle [tx:ty:tz]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01f9d820f27d483153e7e4b0e3ebb3d30fd5e9ae)
![{\displaystyle [x:y:1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbe64dd8a78cef6f5eedea52e24b8452635ea8f9)
![{\displaystyle [x:y:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f368976b6d23da507c1475db79bbf79887eaa9fc)
![{\displaystyle [0:0:0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04de7716a91f28caabdb519e0600751764a66624)























