R*-дерево
| |||||||||||||||||||||||||||||
Read other articles:

Simone Colombi Informasi pribadiTanggal lahir 1 Juli 1991 (umur 32)Tempat lahir Seriate, ItaliaTinggi 1,88 m (6 ft 2 in)Posisi bermain Penjaga gawangInformasi klubKlub saat ini CagliariNomor 1Karier junior AtalantaKarier senior*Tahun Tim Tampil (Gol)2009–2014 Atalanta 0 (0)2009–2010 → Pergocrema (pinjaman) 18 (0)2010 → Alessandria (pinjaman) 2 (0)2011–2012 → Juve Stabia (pinjaman) 39 (0)2012–2013 → Modena (pinjaman) 36 (0)2013–2014 → Padova (pinjaman) ...

Untuk orang lain dengan nama yang sama, lihat Brian Jones (disambiguasi). Brian JonesBrian Jones pada tahun 1965Informasi latar belakangNama lahirLewis Brian Hopkins JonesNama lainElmo LewisLahir(1942-02-28)28 Februari 1942Cheltenham, Gloucestershire, InggrisMeninggal3 Juli 1969(1969-07-03) (umur 27)Hartfield, Sussex Timur, InggrisGenreRock, Rock and roll, Rok biru, Psychedelic rock, R&BPekerjaanMusisi, penulislagu, produser, penggubahInstrumenGitar, Harmonika, Keyboard, Perkusi, Sit...

Liga Champions Wanita UEFA 2022–2023Stadion Philips di Eindhoven menjadi tuan rumah pertandingan finalInformasi turnamenJadwalpenyelenggaraanKualifikasi:18 Agustus – 29 September 2022Kompetisi utama:19 Oktober 2022 – 3 Juni 2023Jumlahtim peserta71 (dari 49 asosiasi)Hasil turnamenJuara Barcelona (gelar ke-2)Tempat kedua VfL WolfsburgStatistik turnamenJumlahpertandingan61Jumlah gol211 (3,46 per pertandingan)Jumlahpenonton681.175 (11.167 per pertandingan)Pencetak golterbanya...

Christopher O'NeillO'Neill di Istana Stockholm, 2013.LahirChristopher Paul O'Neill27 Juni 1974 (umur 49)London, Britania RayaKebangsaanAmerikaInggrisAlmamaterUniversitas BostonSekolah Bisnis ColumbiaGelarHerr (di Swedia)Suami/istriPutri Madeleine, Adipati Hälsingland dan GästriklandAnakPutri Leonore, Adipati GotlandPangeran Nicolas, Adipati ÅngermanlandOrang tuaPaul Cesario O'NeillEva Maria Walter Christopher Paul O'Neill (kelahiran 27 Juni 1974), seorang pengusaha Britania-Amerika, ...

Carla YulesCarla Yules, Miss World Asia 2021.LahirPricilia Carla Yules8 Juli 1996 (umur 27)Surabaya, Jawa Timur, IndonesiaNama lainCarla YulesPendidikan SMP Katolik Santa Agnes Surabaya (2008–2011) SMA Katolik Frateran Surabaya (2011–2014) AlmamaterWilliam Angliss Institute of TAFE, AustraliaPekerjaanmodelratu kecantikanjurutama masakTinggi173 cm (5 ft 8 in)Pemenang kontes kecantikanGelar Miss Sulawesi Selatan 2020 Miss Indonesia 2020 Miss World Indonesia 2021 Wa...

English footballer Tommy Browell Personal informationFull name Thomas BrowellDate of birth (1892-10-19)19 October 1892Place of birth Walbottle, Newcastle upon Tyne, EnglandDate of death 5 October 1955(1955-10-05) (aged 62)Height 5 ft 8 in (1.73 m)[1]Position(s) StrikerSenior career*Years Team Apps (Gls)1910–1911 Hull City 48 (32)1911–1913 Everton 50 (26)1913–1926 Manchester City 222 (122)1926–1930 Blackpool 67 (27)Total 387 (207) *Club domestic league appea...

Area code for east-central Missouri Area codes of Missouri Area code 636 is a telephone area code in North American Numbering Plan (NANP) for the east-central part of the U.S. state of Missouri, comprising mainly the western suburbs of St. Louis. It includes parts of Chesterfield and Fenton in St. Louis County, and all of St. Charles, Jefferson, and Warren counties, all of Franklin County with the exception of Sullivan, as well as the towns of High Hill and Jonesburg in Montgomery County and ...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Pour les articles homonymes, voir Marie et Salope. Une drague aspiratrice et sa marie-salope. Une marie-salope est un chaland destiné à recevoir les vases et sables extraits par dragage[1]. Le mot a vieilli depuis le XIXe siècle au sens de « femme malpropre » ou de « prostituée[2] ». Usage En général, le chargement s'effectue depuis une drague à disque désagrégateur ou depuis une drague à godets, le long de laquelle la marie-salope vient s'amarrer. Lors...

Public university in Arlington, Texas, US The University of Texas at ArlingtonFormer namesArlington College (1895–1902)Carlisle Military Academy (1901–1913)Arlington Training School (1913–1916)Arlington Military Academy (1916–1917)Grubb's Vocational College (1917–1923)North Texas Agricultural College (1923–1949)Arlington State College (1949–1967)MottoDisciplina Praesidium Civitatis (Latin)Motto in EnglishThe cultivated mind is the guardian genius of democracy[1]...
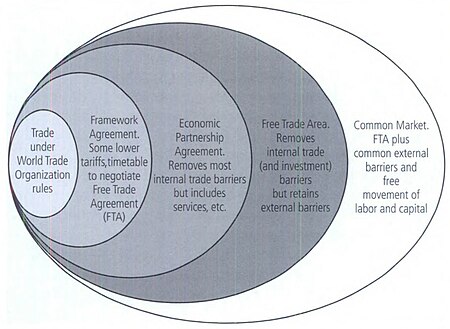
Wide ranging taxes, tariff and trade treaty Part of a series onWorld trade Policy Import Export Balance of trade Trade law Trade pact Trade bloc Trade creation Trade diversion Export orientation Import substitution Trade finance Trade facilitation Trade route Domestic trade Tax Restrictions Trade barriers Tariffs Non-tariff barriers Import quotas Tariff-rate quotas Import licenses Customs duties Export subsidies Technical barriers Bribery Exchange rate controls Embargo Safeguards Countervaili...

María Luisa Albertina de Leiningen-Falkenburg-Dagsburg Princesa de Hesse-Darmstadt Cuadro de Johann Philipp Bach (1792).Información personalOtros títulos Condesa de Leiningen-Falkenburg-DagsburgNacimiento 16 de marzo de 1729Obrigheim, Electorado del PalatinadoFallecimiento 1 de marzo de 1818 (88 años)Neustrelitz, Gran Ducado de Mecklemburgo-StrelitzSepultura Cripta gran ducal de la Iglesia de San Juan Bautista, MirowFamiliaPadre Cristián Carlos Reinardo de Leiningen-Dagsburg-FalkenburgMa...
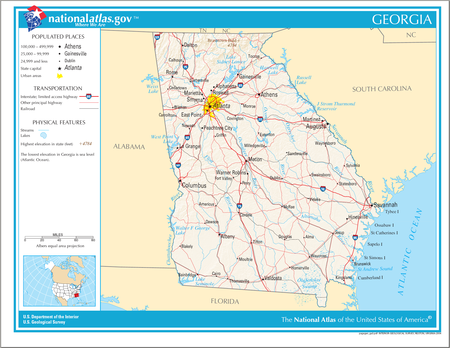
The location of the state of Georgia in the United States of America Main article: Georgia (U.S. state) See also: Outline of Georgia (U.S. state) The following is an alphabetical list of articles related to the U.S. state of Georgia. Contents 0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z See also 0–9 An enlargeable map of the state of Georgia .ga.us – Internet second-level domain for the state of Georgia 4th state to ratify the Constitution of the United States A Adams-Onís ...

AwardShow! Music Core Chart winners (2023) ← 2022 · by year · 2024 → The Show! Music Core Chart is a record chart on the South Korean MBC television music program Show! Music Core. Every week, the show awards the best-performing single on the chart in the country during its live broadcast. In 2023, 29 singles achieved number one on the chart, and 23 acts were awarded first-place trophies. I Am by Ive had the highest score of the year, with 9,668 points on th...

Alessandro Scarlatti Alessandro Scarlatti (Palermo, 2 maggio 1660 – Napoli, 24 ottobre 1725) è stato un compositore italiano di musica barocca. Considerato dai musicologi come uno dei più importanti rappresentanti della scuola musicale napoletana, fu il maggiore compositore d'opera italiano tra la fine del XVII e l'inizio del XVIII secolo. Soprannominato dai suoi contemporanei “l'Orfeo italiano”, divise la sua carriera tra Napoli e Roma, dove ricevette la sua formazione; proprio alla ...

Football league seasonMacedonian First LeagueSeason2023–24Dates6 August 2023 – 18 May 2024ChampionsStruga2nd domestic titleRelegatedMakedonija G.P.BregalnicaChampions LeagueStrugaConference LeagueShkendijaTikveshMatches played198Goals scored446 (2.25 per match)Top goalscorerAleksa Marušić(17 goals)Longest winning run4 gamesAP BreraStrugaShkendijaVoska SportLongest unbeaten run17 gamesGostivarLongest winless run9 gamesAP BreraLongest losing run7 gamesMakedonija G.P.← 2022–23 20...

Years in Russia: 1828 1829 1830 1831 1832 1833 1834 Centuries: 18th century · 19th century · 20th century Decades: 1800s 1810s 1820s 1830s 1840s 1850s 1860s Years: 1828 1829 1830 1831 1832 1833 1834 Sergei Bibikov by Pimen Orlov Events from the year 1831 in Russia. Incumbents Monarch – Nicholas I Events This section needs expansion. You can help by adding to it. (October ...

关于福建历史上的罗江县,请见「罗江县 (孙吴)」。 罗江区市辖区罗江区的地理位置坐标:31°18′19″N 104°30′25″E / 31.30523°N 104.50698°E / 31.30523; 104.50698国家 中华人民共和国隶属行政区四川省德阳市面积 • 总计447.87 平方公里(172.92 平方英里) 人口(2020) • 總計20.91万人时区北京时间(UTC+8)郵政編碼618500行政区�...

Play by Shakespeare Joan la Pucelle redirects here. For the historical figure, the patron saint of France, see Jehanne la Pucelle. For the manuscript illuminator, see Jean Pucelle. First page of The first Part of Henry the Sixt from the First Folio (1623). Henry VI, Part 1, often referred to as 1 Henry VI, is a history play by William Shakespeare—possibly in collaboration with Thomas Nashe and others—believed to have been written in 1591. It is set during the lifetime of King Henry VI of ...

Pour les articles homonymes, voir Irving (homonymie). Washington Irving Portrait de Washington Irving par John Wesley Jarvis, 1809 Données clés Naissance 3 avril 1783 New York, État de New York, États-Unis Décès 28 novembre 1859 (à 76 ans) Sunnyside, État de New York, États-Unis Activité principale essayiste, biographe Auteur Mouvement Fantastique Œuvres principales Le Livre d'esquisses[1] ; La Légende de Sleepy Hollow ; Rip Van Winkle modifier Washington Irving, n...

![R-дерево с квадратным разбиением Гутмана [2]. Есть много страниц, которые распространяются слева направо через всю Германию и страницы сильно перекрываются. Это не вполне благоприятное свойство для большинства приложений, для которых часто нужны только малые прямоугольные области, пересекающиеся со многими полосами.](http://upload.wikimedia.org/wikipedia/commons/thumb/0/0e/Zipcodes-Germany-GuttmanRTree.svg/300px-Zipcodes-Germany-GuttmanRTree.svg.png)
![R-дерево с линейным разбиением Анга-Тана[3]. Хотя прямоугольники не столь протяжёны, как в разбиении Гутмана, проблема разбиения на полосы действует почти на каждый лист на странице. Страницы листов пересекаются мало, но справочные страницы пересекаются сильно.](http://upload.wikimedia.org/wikipedia/commons/thumb/1/19/Zipcodes-Germany-AngTanSplit.svg/300px-Zipcodes-Germany-AngTanSplit.svg.png)
![Топологическое разбиение R* дерева[1]. Страницы перекрываются очень мало, поскольку R*-дерево пытается минимизировать перекрытые страниц, а повторная вставка далее оптимизирует дерево. Стратегия разбиения также не даёт предпочтения полосам, так что получающиеся страницы более пригодны для картографических приложений.](http://upload.wikimedia.org/wikipedia/commons/thumb/c/c7/Zipcodes-Germany-RStarTree.svg/300px-Zipcodes-Germany-RStarTree.svg.png)




