Электромагнитный потенциал
|
Read other articles:

陆军第十四集团军炮兵旅陆军旗存在時期1950年 - 2017年國家或地區 中国效忠於 中国 中国共产党部門 中国人民解放军陆军種類炮兵功能火力支援規模约90门火炮直屬南部战区陆军參與戰役1979年中越战争 中越边境冲突 老山战役 成都军区对越轮战 紀念日10月25日 陆军第十四集团军炮兵旅(英語:Artillery Brigade, 14th Army),是曾经中国人民解放军陆军第十四集团军下属�...

Guest house in Vatican City Domus Sanctae MarthaeThe Domus Sanctae Marthae seen from the dome of St. Peter's BasilicaLocation on a map of Vatican CityGeneral informationTypeResidence, guest houseArchitectural styleModernCountryVatican CityCoordinates41°54′03″N 12°27′12″E / 41.9007°N 12.4533°E / 41.9007; 12.4533Completed1996Opened1996OwnerThe Holy See This article is part of a series onVatican City History Duchy of Rome (533–751) Donation of Pepin (750s) P...

Football league seasonCopa PerúSeason1994ChampionsAtlético TorinoTop goalscorerRichard Vinatea (6)← 1993 1995 → The 1994 Copa Perú season (Spanish: Copa Perú 1994), the promotion tournament of Peruvian football. In this tournament after many qualification rounds, each one of the 24 departments in which Peru is politically divided, qualify a team. Those teams plus the team relegated from First Division are divided in 6 groups by geographical proximity and each group winner goes to the ...

Paul NewmanNewman pada tahun 1958LahirPaul Leonard Newman26 Januari 1925Shaker Heights, Ohio, Amerika SerikatMeninggal26 September 2008Westport, Connecticut, Amerika SerikatSebab meninggalKanker paru-paruPendidikanKenyon College (BA) Universitas YaleDikenal atasPemeran Lucas Luke Jackson dalam Cool Hand Luke Henry Gondorff dalam The Sting Pengisi Suara Doc Huson dalam CarsTinggi177 cm (5 ft 10 in)Suami/istriJackie Witte (1949–1958) Joanne Woodward (1958–2008)Anak6Peng...

Men's points race at the 2018 UEC European Track ChampionshipsVenueSir Chris Hoy Velodrome, GlasgowDate5 AugustCompetitors18 from 18 nationsWinning points102Medalists Wojciech Pszczolarski Poland Kenny De Ketele Belgium Stefan Matzner Austria← 20172019 → 2018 UEC EuropeanTrack ChampionshipsSprintmenwomenTeam sprintmenwomenTeam pursuitmenwomenKeirinmenwomenOmniummenwomenMadisonmenwomenTime trialmenwo...

American politician For the American volleyball player, see Russell Holmes (volleyball). This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Russell Holmes – news · newspapers · books · scholar · JS...

Yoizuki di Kure pada 16 Oktober 1945 Sejarah Kekaisaran Jepang Nama YoizukiPembangun Perusahaan Dok UragaPasang lunas 25 Agustus 1943Diluncurkan 25 September 1944Selesai 31 Januari 1945Mulai berlayar 31 Januari 1945Dicoret 5 Oktober 1945Nasib Ditransfer ke Tiongkok pada 29 Agustus 1947Catatan Skuadron Perusak ke-11 Taiwan Nama Fen YangDiperoleh 29 Agustis 1947Mulai berlayar February 1949Dicoret 1963Nasib Dibesituakan pada 1963Catatan Armada Pelatihan Ciri-ciri umum Kelas dan jenis Kapal peru...

Toro Rosso STR12 Carlos Sainz Jr. alla guida della STR12 nei test prestagionali di Barcellona Descrizione generale Costruttore Toro Rosso Categoria Formula 1 Squadra Scuderia Toro Rosso Progettata da James KeyBen WaterhousePaolo MarabiniMark TathamBrendan Gilhome Sostituisce Toro Rosso STR11 Sostituita da Toro Rosso STR13 Descrizione tecnica Meccanica Telaio monoscocca in fibra di carbonio Motore Renault Trasmissione Cambio sequenziale a 8 rapporti + retromarcia Dimensioni e pesi Lungh...

Scottish surgeon, anatomist, artist and theologian For other people named Charles Bell, see Charles Bell (disambiguation). Sir Charles BellKH FRS FRSE FRCSEBorn(1774-11-12)12 November 1774Edinburgh, ScotlandDied28 April 1842(1842-04-28) (aged 67)Hallow, Worcestershire, EnglandNationalityScottishAlma materUniversity of EdinburghKnown forauthority on the human nervous systemAwardsRoyal Medal (1829)Scientific careerFieldsAnatomyInstitutionsSurgeon, Edinburgh Royal Infirmary (1799�...
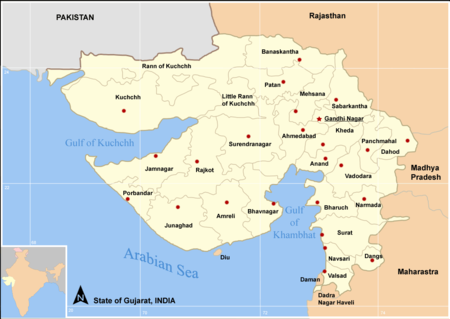
This article needs to be updated. Please help update this article to reflect recent events or newly available information. (June 2021) DamKalpasar DamLocation of Kalpasar Dam in IndiaCoordinates21°27′21″N 72°24′57″E / 21.45583°N 72.41583°E / 21.45583; 72.41583WebsiteOfficial website The Gulf of Khambat is at the right-lower-center of the map of Gujarat on the Arabian Sea. The Kalpasar Project or the Gulf of Khambhat Development Project envisages building a...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Fondation des Parkings Logo de la Fondation des Parkings. Le siège de la Fondation, au sommet du P+R Étoile Création 1969 Forme juridique Fondation Siège social Canton de Genève Suisse Direction Damien Zuber (depuis 2020)[1] Activité Construction et exploitation de parkingsPrestations de services en matière de stationnement Effectif 190 Site web www.geneve-parking.ch modifier - modifier le code - voir Wikidata La Fondation des Parkings est un établissement autonome de droi...

2022年肯塔基州聯邦參議員選舉 ← 2016年 2022年11月8日 (2022-11-08) 2028年 → 获提名人 蘭德·保羅 查爾斯·布克 政党 共和黨 民主党 民選得票 913,326 564,311 得票率 61.8% 38.2% 各縣結果保羅: 50–60% 60–70% 70–80% 80–90%布克: 50–60% 60–70% 选前聯邦參議...

Spurline TrailView looking south on the trail just to the north of Ferdinand Avenue.Length2.4 km (1.5 mi)LocationWaterloo and Kitchener, Ontario, CanadaEstablished2016TrailheadsWaterloo: Laurel Trail near Waterloo City HallKitchener: Ahrens Street WestUse Walking cycling SurfaceAsphaltRight of wayCN Waterloo SpurMaintained byCity of KitchenerCity of Waterloo The Spurline Trail is a multi-use urban rail with trail which connects the cities of Waterloo and Kitchener, Ontario, Canada. ...

La Constitutio Antoniniana sous vitrine climatisée L'édit de Caracalla de 212, également appelé Constitution antonine (en latin : Constitutio Antoniniana), est une des lois les plus connues de l'Empire romain. Promulgué par Caracalla, empereur romain de 211 à 217, il accorde, à la date de promulgation de l'édit, la citoyenneté romaine à tout homme libre de l'Empire qui ne l'avait pas encore acquise. La citoyenneté romaine est héréditaire, par la filiation et l'adoption. Long...

BBC's online searchable database of programme listings between 1923 and 2009 Logo of the BBC Genome Project The BBC Genome Project is an online searchable database of programme listings initially based upon the contents of the Radio Times from the first issue in 1923 to 2009.[1] Television listings from post-2009 can be accessed via the BBC Programmes site.[2] History Prior BBC Genome is not the BBC's first online searchable database. In April 2006, they gave the public access...

لمعانٍ أخرى، طالع فالكون (توضيح). فالكون الإحداثيات 34°23′36″N 90°15′21″W / 34.3933°N 90.2558°W / 34.3933; -90.2558 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كيتمان خصائص جغرافية المساحة 1.012785 كيلومتر مربع1.012784 كيلومتر مرب�...

Peta wilayah Komune Verano Brianza (merah) di Provinsi Monza dan Brianza (emas), Lombardia, Italia. Verano Brianza komune di Italia Tempat Negara berdaulatItaliaDaerah di ItaliaLombardyProvinsi di ItaliaProvinsi Monza dan Brianza NegaraItalia Ibu kotaVerano Brianza PendudukTotal9.137 (2023 )GeografiLuas wilayah3,52 km² [convert: unit tak dikenal]Ketinggian264 m Berbatasan denganBriosco Giussano Carate Brianza SejarahSanto pelindungNazarius and Celsus (en) Informasi tambahanKode po...

Village in Wales This article is about the community and village in Wales. For the locality in Western Australia, see Ruabon, Western Australia. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Ruabon – news · newspapers · books · scholar · JSTOR (December 2011) (Learn how and when to remove this message) Hum...

紀是中國古代曆法的時間單位。指蔀之日數與60個干支紀日之最短循環週期[1]。 文內注釋 ^ 後漢書. 卷93志第三《律曆下》: 日周於天,一寒一暑,四時備成,萬物畢改,攝提遷次,青龍移辰,謂之歲。歲首至也,月首朔也。至、朔同日謂之章,同在日首謂之蔀,蔀終六旬謂之紀,歲朔又復謂之元。 查论编时间基本概念 历史 過去 現在 未来 永恆 时间箭头 时间单位�...



































