Теорема о распределении простых чисел
|
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Marcelo Peralta – berita · surat kabar · buku · cendekiawan · JSTOR (March 2020) Marcelo Peralta (5 Maret 1961 – 10 Maret 2020)) adalah pemain musik, guru, komposer, dan arranger dari Argentin...

Kenidai Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Plantae Divisi: Magnoliophyta Kelas: Magnoliopsida Ordo: Malpighiales Famili: Phyllanthaceae Tribus: Bridelieae Genus: Bridelia Spesies: Bridelia tomentosaBlume Sinonim Bridelia tomentosa nayarii (P.Basu) Chakrab., M.Gangop. & N.P.Balakr.Bridelia loureiroi Müll.Arg., sphalm.Bridelia urticoides Griff.Bridelia tomentosa trichadenia Müll.Arg.Bridelia tomentosa rhamnoides (Griff.) Müll.Arg.Bridelia tomentosa ovoidea Benth.Bridelia tom...

Group of international day and boarding schools This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: TASIS Schools – news · newspapers · books · scholar · JSTOR (August 2020) (Learn how and when to remove this template message) TASIS SchoolsTASIS FoundationInformationTypeGroup of international boarding schoolsEst...

Dedalu tangis Salix babylonica Status konservasiKekurangan dataIUCN61960227 TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladSuperrosidaeKladrosidsKladfabidsOrdoMalpighialesFamiliSalicaceaeGenusSalixSpesiesSalix babylonica Linnaeus, 1753 Tata namaSinonim takson Daftar Ficus salix H.Lév. & Vaniot Salix babylonica var. glandulipilosa P.I.Mao & W.Z.Li Salix cantoniensis Hance Salix capitata Y.L.Chou & Skvortsov Sali...

Administrative district within the Spanish Empire (1777–1834) This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (April 2015) (Learn how and when to remove this template message) Captaincy General of VenezuelaCapitanía General de Venezuela1777–1824 Coat of arms of Caracas Anthem: Marcha RealRoyal MarchFlag of Spain: first national flag, naval flag since...

Keluarga Yasin Limpo merujuk kepada keluarga besar keturunan Kol. (Purn) H.M. Yasin Daeng Limpo dan Hj. Nurhayati, yang berasal dari Sulawesi Selatan.[1][2] Keluarga ini memegang banyak posisi penting di bidang pemerintahan dan politik, yang umumnya melalui jalur kader Partai Golkar Sulawesi Selatan,[1][2] meskipun ada pula yang melalui Partai Amanat Nasional (PAN) dan Partai Hati Nurani Rakyat (Hanura) seperti Dewi Yasin Limpo.[3] Anggota keluarga Syah...
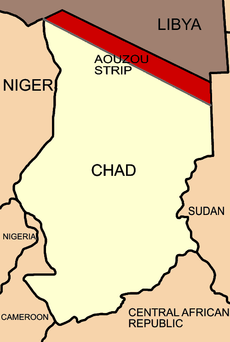
Resolusi 926Dewan Keamanan PBBKawasan Jalur AouzouTanggal13 Juni 1994Sidang no.3.389KodeS/RES/926 (Dokumen)TopikChad-Jamahiriya Arab LibyaRingkasan hasil15 mendukungTidak ada menentangTidak ada abstainHasilDiadopsiKomposisi Dewan KeamananAnggota tetap Tiongkok Prancis Rusia Britania Raya Amerika SerikatAnggota tidak tetap Argentina Brasil Republik Ceko Djibouti Spanyol Nigeria Selandia Baru Oman Pakistan Rwan...

Mauro Corona Mauro Corona nell'ottobre 2013 al Premio Chiara Nazionalità Italia Alpinismo Modifica dati su Wikidata · Manuale Mauro Corona, all'anagrafe Maurizio Corona (Baselga di Piné, 9 agosto 1950), è uno scrittore, alpinista e scultore ligneo italiano. Autore di svariati libri, alcuni dei quali best seller, si è dedicato all'alpinismo, scalando numerose vette italiane ed estere e aprendo oltre 300 vie di arrampicata nelle Dolomiti Friulane. Indice 1 Biografia 1.1 ...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Evolusi Jangka Panjang – berita · surat kabar · buku · cendekiawan · JSTOR 3GPP Long Term Evolution atau yang biasa disingkat LTE adalah sebuah standar komunikasi akses data nirkabel tingkat tinggi yang ...

Satirical magazine Modern DrunkardCover of the May 2003 issue of Modern DrunkardTypeMagazineFormatBroadsheetPublisherFrank Kelly RichEditorFrank Kelly RichFounded1996HeadquartersDenver, ColoradoWebsitedrunkard.com Modern Drunkard is a glossy color periodical humorously promoting the lifestyle of the functional alcoholic.[1][2] History Frank Kelly Rich founded Modern Drunkard in 1996. The first issue was 16 photocopied pages with made-up ads; in 2006 its circulation was about 3...

Vicherey L'église Saint-Remy. Blason Administration Pays France Région Grand Est Département Vosges Arrondissement Neufchâteau Intercommunalité Communauté de communes du Pays de Colombey et du Sud Toulois Maire Mandat Alain Abscheidt 2020-2026 Code postal 88170 Code commune 88504 Démographie Gentilé Viscariens, Viscariennes Populationmunicipale 174 hab. (2021 ) Densité 30 hab./km2 Géographie Coordonnées 48° 23′ 02″ nord, 5° 56′ 15″ ...

Ank BijleveldBijleveld pada 2018 Menteri PertahananMasa jabatan26 Oktober 2017 – 17 September 2021Perdana MenteriMark RuttePendahuluKlaas DijkhoffPenggantiFerdinand Grapperhaus (ad interim)Komisioner Raja OverijsselMasa jabatan1 Januari 2011 – 26 Oktober 2017Penguasa monarkiBeatrix (2011–2013) Willem-Alexander (2013–2017)PendahuluGeert JansenPenggantiAndries HeidemaSekretaris Negara untuk Dalam Negeri dan Hubungan KerajaanMasa jabatan22 February 2007 – 14 ...

Type of pastoralism Seter redirects here. For other uses, see Seter (disambiguation). Not to be confused with Transhumanism. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article appears to be slanted towards recent events. Please try to keep recent events in historical perspective and add more content related to non-recent events. (June 2018) This article needs additional citation...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

Северный морской котик Самец Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапси...

Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. Будь ласка, допоможіть удосконалити цю статтю, додавши посилання на надійні (авторитетні) джерела. Зверніться на сторінку обговорення за поясненнями та допоможіть виправити недоліки. Мат...

طواف النرويج 2021 تفاصيل السباقسلسلة10. طواف النرويجمنافسةسلسلة سباقات الاتحاد الدولي للدراجات للمحترفين 2021 2.Proمراحل4التواريخ19 – 22 أغسطس 2021المسافات634٫88 كمالبلد النرويجنقطة البدايةإغرسوندنقطة النهايةستافانغرالفرق19عدد المتسابقين في البداية113عدد المتسابقين في النهاي�...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Neemrana – news · newspapers · books · scholar · JSTOR (January 2018) (Learn how and when to remove this me...

Lars Løkke Rasmussen Perdana Menteri DenmarkMasa jabatan28 Juni 2015 – 27 Juni 2019Penguasa monarkiMargrethe IIPendahuluHelle Thorning-SchmidtPenggantiMette FrederiksenMasa jabatan5 April 2009 – 3 Oktober 2011Penguasa monarkiMargrethe IIWakilLene EspersenLars BarfoedPendahuluAnders Fogh RasmussenPenggantiHelle Thorning-SchmidtMenteri Keuangan DenmarkMasa jabatan23 November 2007 – 7 April 2009Perdana MenteriAnders Fogh RasmussenPendahuluThor PedersenPenggantiC...

![{\displaystyle [1;n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc1323b99eabd379a2588017a0cf9981027405d8)






















![{\displaystyle [1,n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c79af450e22e8fd23f28e6be4cb23a47b24c1ba)





















































