Плоскость Фано
|
Read other articles:
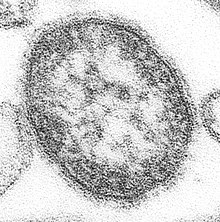
Rougeole Exanthème morbilliforme, éruption typique de rougeole. Données clés Causes Virus de la rougeole (Genre Morbillivirus / Famille Paramyxoviridae) Transmission Transmission aéroportée (d) Incubation min 6 j ou 7 j Incubation max 19 j ou 21 j Symptômes Fièvre, toux, rhinorrhée, éruption maculopapuleuse (en), adénopathie, anorexie, diarrhée, Signe de Köplik, conjonctivite et catarrhe oculo-nasal (d) Traitement Prévention Vaccination Traitement Soins de support (d) Spéciali...

Artikel ini bukan mengenai Alexandria. AlessandriaKomuneComune di AlessandriaNegara ItaliaWilayahPiedmontProvinsiAlessandria (AL)Zona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos15121-15122Kode area telepon0131Situs webwww.comune.alessandria.it Alessandria (bahasa Piemonte: Lissandria) merupakan nama kota di Italia. Letaknya di bagian barat. Tepatnya di region Piemonte, Italia. Pada tahun 2005, kota ini memiliki jumlah penduduk sebanyak 91.593 jiwa dengan memiliki...

New Hampshire gubernatorial election 1828 New Hampshire gubernatorial election ← 1827 March 11, 1828 1829 → Nominee John Bell Benjamin Pierce Party Anti-Jacksonian Jacksonian Popular vote 21,149 18,672 Percentage 53.01% 46.80% Governor before election Benjamin Pierce Jacksonian Elected Governor John Bell Anti-Jacksonian Elections in New Hampshire Federal government Presidential elections 1788–89 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 18...

Greek politicianIoannis OrlandosIoannis Orlandosby Konstantinos PalaiologosNative nameΙωάννης ΟρλάνδοςBorn1770Spetses, Ottoman Empire (now Greece)Died1852Hydra, Kingdom of GreeceAllegiance First Hellenic Republic Kingdom of Greece Battles/warsGreek War of IndependenceOther workDelegate at the First National Assembly at EpidaurusFounding member of the Archaeological Society of Athens Ioannis Orlandos (Greek: Ιωάννης Ορλάνδος) was a Greek politician and revolu...

Czechoslovak laws (1940–45) Beneš decreesEdvard Beneš, 1935–1938 and 1940–1948 President of CzechoslovakiaNational Assembly of the Czechoslovak Republic Long title Decrees of the President of the Republic Enacted byNational Assembly of the Czechoslovak RepublicIntroduced byCzechoslovak government-in-exile The Beneš decrees[a] were a series of laws drafted by the Czechoslovak government-in-exile in the absence of the Czechoslovak parliament during the German occupation of...

Caravanserai in Razavi Khorasan Province, IranAmin al-tojar Caravansaraiکاروانسرای امین التجارGeneral informationTypeCaravanseraiArchitectural styleQajar architectureLocationKashmar, Razavi Khorasan Province, IranCoordinates35°13′59.71″N 58°27′44.25″E / 35.2332528°N 58.4622917°E / 35.2332528; 58.4622917Construction startedQajar dynasty Amin al-tojar Caravansarai (Persian: کاروانسرای امین التجار) is a caravanserai rela...

Les MesneuxcomuneLes Mesneux – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementReims CantoneFismes-Montagne de Reims TerritorioCoordinate49°13′N 3°58′E / 49.216667°N 3.966667°E49.216667; 3.966667 (Les Mesneux)Coordinate: 49°13′N 3°58′E / 49.216667°N 3.966667°E49.216667; 3.966667 (Les Mesneux) Superficie4,27 km² Abitanti875[1] (2009) Densità204,92 ab./km² Altre informazioniCod. ...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Земская почтаУезды Алатырский Александрийский Ананьевский Ардатовский Арзамасский Аткарский Ахтырский Балашовский Бахмутский Бежецкий Белебеевский Белозерский Бердянский Бобровский Богородский Богучарский Борисоглебский Боровичский Бронницкий Бугульминский Бу�...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Cape Verde–China relations – news · newspapers · books · scholar · JSTOR (February 2022) You can help expand this article with text translated from the corresponding article in Chinese. (March 2023) Click [show] for important translation instru...

Untuk karakter mata-mata fiksi, lihat Bill Haydon. William Hayden beralih ke halaman ini. Untuk Ajudan Jenderal Negara Bagian Connecticut, lihat William Hayden (prajurit). Bill HaydenAC Gubernur Jenderal Australia ke-21Masa jabatan16 Februari 1989 – 16 Februari 1996Penguasa monarkiElizabeth IIPerdana MenteriBob Hawke Paul KeatingPendahuluSir Ninian StephenPenggantiSir William DeanePemimpin OposisiMasa jabatan22 Desember 1977 – 3 Februari 1983Penguasa monarkiElizabeth IIG...

Form of slavery Part of a series onForced labour and slavery Contemporary Child labour Child soldiers Conscription Debt Forced marriage Bride buying Child marriage Wife selling Forced prostitution Human trafficking Peonage Penal labour Contemporary Africa 21st-century jihadism Sexual slavery Wage slavery Historical Antiquity Egypt Babylonia Greece Rome Medieval Europe Ancillae Black Sea slave trade Byzantine Empire Kholop Prague slave trade Serfs History In Russia Emancipation Thrall Venetian...

Defunct Christian denomination in the United States For the national Lutheran church of Finland, see Evangelical Lutheran Church of Finland. Finnish Evangelical Lutheran Church of AmericaOld Main at the FELC's Suomi College in Hancock, MichiganClassificationProtestantOrientationLutheranRegionMichigan and other statesHeadquartersCalumet, MichiganOriginMarch 25, 1890 Calumet, MichiganBranched fromEvangelical Lutheran Church of FinlandMerged intoLutheran Church in America (1962)Congregations153 ...

County in Florida, United States County in FloridaLevy CountyCountyLevy County CourthouseLocation within the U.S. state of FloridaFlorida's location within the U.S.Coordinates: 29°17′N 82°47′W / 29.28°N 82.79°W / 29.28; -82.79Country United StatesState FloridaFoundedMarch 10, 1845Named forDavid Levy YuleeSeatBronsonLargest cityWillistonArea • Total1,413 sq mi (3,660 km2) • Land1,118 sq mi (2,900 km...

Tyne and Wear Metro and railway station in Gateshead HeworthTyne and Wear Metro stationGeneral informationLocationHeworth, GatesheadEnglandCoordinates54°57′05″N 1°33′21″W / 54.9515°N 1.5559°W / 54.9515; -1.5559Grid referenceNZ285619Transit authorityTyne and Wear PTEPlatforms2Tracks2Bus stands7ConstructionParking463 spacesBicycle facilities 4 cycle lockers 25 cycle racks AccessibleStep-free access to platformOther informationStation codeHEWFare zoneBHistory...

U.S. presidential administration from 1901 to 1909 For a chronological guide, see Timeline of the Theodore Roosevelt presidency. Presidency of Theodore RooseveltSeptember 14, 1901 – March 4, 1909CabinetSee listPartyRepublicanElection1904SeatWhite House← William McKinleyWilliam Howard Taft → Seal of the president(1894–1945)Library website This article is part of a series aboutTheodore Roosevelt Political positions Electoral history Early life Family The Naval...

1998 United States law Federal Vacancies Reform Act of 1998Enacted bythe 105th United States CongressCitationsPublic lawPub. L.Tooltip Public Law (United States) 105–277 (text) (PDF)Legislative historyIntroduced in the House as Sec. 151 of Division C of the Omnibus Consolidated and Emergency Supplemental Appropriations Act, 1999 (H.R. 4328)Passed the House on October 20, 1998 (333–95)Passed the Senate on October 21, 1998 (65–29)Signed into law by President Bill ...

American poet Minot Judson Savage Minot Judson Savage (June 10, 1841 – May 22, 1918) was an American Unitarian minister, psychical researcher and author. Biography Savage was born in Norridgewock, Maine in 1841. He graduated from the Bangor Theological Seminary in 1864, and for nine years was in the Congregational ministry, being a home missionary at San Mateo and Grass Valley, California, until 1867. He held pastorates at Framingham, Massachusetts from 1867 to 1869, and at Hannibal, Missou...

Road in New Zealand Johnsonville–Porirua MotorwayState Highway 1 / State Highway 59Route informationLength11 km (6.8 mi)Existed23 December 1950–presentMajor junctionsNorth endPoriruaSouth endJohnsonville LocationCountryNew ZealandPrimarydestinationsTawa, Churton Park, Grenada North Highway system New Zealand state highways Motorways and expressways List Aerial view of the Johnsonville-Porirua Motorway in southeastern Linden The Johnsonville–Porirua Motorway is a...

Public university in England This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: University of Leicester – news · newspapers · books · scholar · JSTOR (May 2018) (Learn how and when to remove this message) University of LeicesterShield of the University of LeicesterMottoLatin: Ut Vitam HabeantMotto in Engli...




