ŠŠøŠ»ŃŠ¼Š½Š¾Š³Š¾Š¾Š±ŃŠ°Š·ŠøŠµ
|
Read other articles:

Damian PriestPriest pada tahun 2017Nama lahirLuis MartĆnez[1]Lahir26 September 1982 (umur 41)New York City, A.S.[2]Karier gulat profesionalNama ringDamian Martinez[1]Damian PriestLuis Martinez[1]Punisher Martinez[1]Punishment Martinez[1]Tinggi6 ft 5 in (1,96 m)[3]Berat249 pon (113 kg)[3]Asal dariNew York CityDilatih olehMonster Factory[1]Debut25 Maret 2005[4] Luis MartĆnez[1]...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. FBFC (Fabrikasi Franco-Belge de Fabrication du Flustible, Prancis-Belgia) adalah perusahaan pembuat bahan bakar nuklir. Dari tahun 1977 dan seterusnya kantor pusatnya berlokasi di Romans-sur-IsĆØre. Perusahaan mengoperasikan dua fasilitas lagi, satu di...

Ini adalah daftar film yang diproduksi atau didistribusikan oleh Warner Bros., didirikan pada tahun 1918 sebagai Warner Bros. Pictures. Ini adalah lengan produksi dan distribusi film utama Warner Bros., anak perusahaan dari divisi WarnerMedia. Kata kunci Keterangan: (DP (....)) = diproduksi bersama (D) = distribusi (DS (......)) = hanya distribusi dan produksi (DS-USA) = distribusi di Amerika Serikat (FR) = film negara asing (DDP (......) (distributor tambahan); (......) (produser)) kerja sam...

High School in Chicago, Illinois, United States Harlan Community Academy High SchoolAddress9652 South Michigan AvenueChicago, Illinois 60628United StatesCoordinates41Ā°43ā²07ā³N 87Ā°37ā²17ā³W / 41.7185Ā°N 87.6213Ā°W / 41.7185; -87.6213InformationSchool typePublicSecondaryOpened1958School districtChicago Public SchoolsPrincipalKai L. Jones[1]Grades9ā12GenderCoedEnrollment273 (2022ā2023)[1]Campus typeUrbanColor(s) Blue White[2]...

éåļ¼é¦¬ä¾č„æäŗéäæ 马ę„č„æäŗ é©å½ 代č”Øę©ę§é©¬ę„č„æäŗé©»é©å½å¤§ä½æé¦é©å½é©»é©¬ę„č„æäŗ大ä½æé¦ é©å½ļ¼é©¬ę„č„æäŗå ³ē³»ļ¼é©čÆļ¼ėķėƼźµ-ė§ė ģ“ģģ ź“ź³ļ¼é¦¬ä¾čŖļ¼Hubungan Korea SelatanāMalaysiaļ¼ļ¼äŗ¦ē§°é©¬ę„č„æäŗļ¼é©å½å ³ē³»ļ¼ęé©å½äø马ę„č„æäŗäø¤å½ä¹é“ēåč¾¹å ³ē³»ćē®åäø¤å½äøŗāęē„ä¼ä¼“å ³ē³»āć åå² é©å½äø马ę„äŗčåé¦äŗ1960幓2ę23ę„å»ŗäŗ¤[1]ć1962幓5ęļ¼é©å½åØ马ę„äŗé¦é½å...

Historic house in Washington, D.C., United States United States historic placeThomas Law HouseU.S. National Register of Historic Places The Thomas Law House in 2019Location1252 6th Street, S.W.Washington, D.C.Coordinates38Ā°52ā²29.3ā³N 77Ā°01ā²11ā³W / 38.874806Ā°N 77.01972Ā°W / 38.874806; -77.01972ArchitectWilliam LoveringArchitectural styleFederalNRHP reference No.73002093Added to NRHPAugust 14, 1973 The Thomas Law House (Honeymoon House) was constr...

Legal rules pertaining to familial relationships South African family law is concerned with those legal rules in South Africa which pertain to familial relationships.[1] It may be defined as that subdivision of material private law which researches, describes and regulates the origin, contents and dissolution of all legal relationships between: (i) husband and wife (including the parties to a civil union); (ii) parents, guardians (and other holders of parental rights and responsibilit...

Ł ŁŁŲ² Ų¹Ł Ų¹ŲØŲÆ Ų§ŁŁŁ ŲØŁ Ų¹ŲØŲÆ Ų§ŁŁŁ ŲØŁ Ų«ŁŁŲ§Ł Ų¢Ł Ų³Ų¹ŁŲÆ. Ų£Ł ŁŲ± ŁŲ¬ŲÆ ŁŲ§ŁŲ§ŲŲ³Ų§Ų” Ų¹ŲØŲÆ Ų§ŁŁŁ ŲØŁ Ų«ŁŁŲ§Ł ŲØŁ Ų„ŲØŲ±Ų§ŁŁŁ Ų§Ł Ų«ŁŁŲ§Ł Ų¢Ł Ų³Ų¹ŁŲÆ Ų£Ł ŁŲ± Ų§ŁŲÆŁŁŲ© Ų§ŁŲ³Ų¹ŁŲÆŁŲ© Ų§ŁŲ«Ų§ŁŁŲ© Ų§ŁŲ®Ų§Ł Ų³ Ų§ŁŲŲ§ŁŁ Ų§ŁŲ¹Ų§Ų“Ų± Ł Ł Ų¢Ł Ų³Ų¹ŁŲÆ ŁŲŖŲ±Ų© Ų§ŁŲŁŁ 1257 ŁŁ - 1259 ŁŁ Ų®Ų§ŁŲÆ ŲØŁ Ų³Ų¹ŁŲÆ ŁŁŲµŁ ŲØŁ ŲŖŲ±ŁŁ Ł Ų¹ŁŁŁ Ų§ŲŖ Ų“Ų®ŲµŁŲ© ŲŖŲ§Ų±ŁŲ® Ų§ŁŁ ŁŁŲ§ŲÆ 2 Ų£ŁŁŁŲ© Ų§ŁŁŁŲ§Ų© 1259 ...

1987 English local election This article relies largely or entirely on a single source. Please help improve this article by introducing citations to additional sources.Find sources: 1987 Worthing Borough Council election ā news Ā· newspapers Ā· books Ā· scholar Ā· JSTOR (December 2023) 1987 Worthing Borough Council election ← 1986 7 May 1987 (1987-05-07) 1988 → 12 out of 36 seats to Worthing Borough Council19 seats need...

åéæåęÆä½©å °čØBoa EsperanƧaåøéåéæåęÆä½©å °čØåØå·“č„æēä½ē½®åę ļ¼21Ā°05ā²24ā³S 45Ā°33ā²57ā³W / 21.09Ā°S 45.565833333333Ā°W / -21.09; -45.565833333333å½å®¶å·“č„æå·ē±³ēŗ³ęÆåęęÆå·é¢ē§Æ ā¢ ę»č®”858.728 å¹³ę¹å ¬éļ¼331.557 å¹³ę¹č±éļ¼ęµ·ę775 å ¬å°ŗļ¼2,543 č±å°ŗļ¼äŗŗå£ ā¢ ēø½čØ37,801äŗŗ ā¢ åÆåŗ¦44äŗŗ/å¹³ę¹å ¬éļ¼114äŗŗ/å¹³ę¹č±éļ¼ åéæåęÆä½©å °čØļ¼č”čļæ½...

FusagasugĆ” Municipio Templo Nuestra SeƱora de BelĆ©n BanderaEscudo FusagasugĆ”LocalizaciĆ³n de FusagasugĆ” en Colombia FusagasugĆ”LocalizaciĆ³n de FusagasugĆ” en Cundinamarca Coordenadas 4Ā°20ā²14ā³N 74Ā°21ā²52ā³O / 4.3372222222222, -74.364444444444Entidad Municipio ā¢ PaĆs Colombia ā¢ Departamento Cundinamarca ā¢ Provincia SumapazAlcalde William GarcĆa Fayad (2024-2027)Eventos histĆ³ricos ā¢ FundaciĆ³n 5 de febrero de 1592 (432 aƱo...

Austrian-American scholar This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (March 2016) (Learn how and when to remove this message) Gerda LernerGerda Kronstein in 1981.BornGerda Hedwig Kronstein(1920-04-30)April 30, 1920Vienna, AustriaDiedJanuary 2, 2013(2013-01-02) (aged 92)Madison, Wisconsin, U.S.EducationNew School (BA)Columbia University (MA, PhD)Spous...
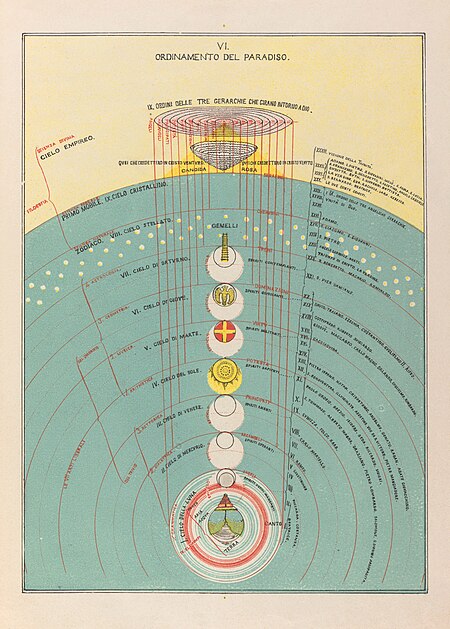
Hermetic starfire body For other uses, see Astral body (disambiguation). La materia della Divina commedia di Dante Alighieri, Plate VI: The Ordering of Paradise by Michelangelo Caetani (1804ā1882) Part of a series onThelemaUnicursal hexagram The Rights of Man Holy Books and Stele The Book of the Law The Holy Books of Thelema The Stele of Revealing Key figures Ankh-af-na-Khonsu FranƧois Rabelais Aleister Crowley Victor Neuburg Charles Stansfeld Jones Jack Parsons Wilfred Talbot Smith Jane W...

ŁŁ Ų¹Ų§ŁŁ Ų£Ų®Ų±ŁŲ Ų·Ų§ŁŲ¹ ŲŁŲÆŲ± Ų¢ŲØŲ§ŲÆ (ŲŖŁŲ¶ŁŲ). ŲŁŲÆŲ± Ų¢ŲØŲ§ŲÆ ŲŖŲ§Ų±ŁŲ® Ų§ŁŲŖŲ£Ų³ŁŲ³ 1768 ŲŖŁŲ³ŁŁ Ų„ŲÆŲ§Ų±Ł Ų§ŁŲØŁŲÆ ŲØŲ§ŁŲ³ŲŖŲ§Ł [1][2] Ų®ŲµŲ§Ų¦Ųµ Ų¬ŲŗŲ±Ų§ŁŁŲ© Ų„ŲŲÆŲ§Ų«ŁŲ§ŲŖ 25Ā°22ā²45ā³N 68Ā°22ā²06ā³E / 25.379166666667Ā°N 68.368333333333Ā°E / 25.379166666667; 68.368333333333 Ų§ŁŁ Ų³Ų§ŲŲ© 319 ŁŁŁŁŁ ŲŖŲ± Ł Ų±ŲØŲ¹ Ų§ŁŲ§Ų±ŲŖŁŲ§Ų¹ 13 Ł ŲŖŲ± Ų§ŁŲ³ŁŲ§Ł Ų§ŁŲŖŲ¹ŲÆŲ§...

Egyptian Islamic scholar (1372ā1449) For the 16th-century Sunni Muslim Shafi'i scholar, see Ibn Hajar al-Haytami. ImamIbn Hajar al-AsqalaniŲ§ŲØŁ ŲŲ¬Ų± Ų§ŁŲ¹Ų³ŁŁŲ§ŁŁTomb of Ibn Hajar al-Asqalani in CairoTitleShaykh al-IslamHafizPersonalBorn18 February 1372 (1372-02-18)Cairo, Mamluk SultanateDied2 February 1449 (1449-02-03) (aged 76)[7]Cairo, Mamluk SultanateResting placeCity of the Dead, Cairo, EgyptReligionIslamEra Bahri Era Burji Era DenominationSunniJurisprud...

Swedish ice hockey player Ice hockey player Viktor Lƶƶv Viktor Lƶƶv in 2013Born (1992-11-16) 16 November 1992 (age 31)SƶdertƤlje, SwedenHeight 1.91 m (6 ft 3 in)Weight 98 kg (216 lb; 15 st 6 lb)Position DefenceShoots LeftNL teamFormer teams EHC BielSƶdertƤlje SKModo HockeyToronto Maple LeafsJokeritNational team SwedenNHL draft 209th overall, 2012Toronto Maple LeafsPlaying career 2011–present Viktor Lƶƶv (born 16 November 1992) is a...

French naval strategy The Jeune Ćcole (Young School) was a strategic naval concept developed during the 19th century. It advocated the use of small, heavily armed vessels to combat larger battleships, and the use of commerce raiders to cripple the trade of the rival nation. The idea was developed among French naval theorists: the French government had the second largest navy of the time, and the theorists desired to counteract the strength of the larger British Royal Navy. Small units agains...

State governed as a single unit with a supreme central government Unitary states Federal states Part of the Politics seriesBasic forms of government List of forms of government List of countries by system of government Source of power Democracy (rule by many) Demarchy Direct Economic Liberal Representative Social Socialist Others Oligarchy (rule by few) Anocracy Aristocracy Gerontocracy Kleptocracy Kritarchy Meritocracy Noocracy Particracy Plutocracy Stratocracy Techno...

German geologist (1808ā1879) Bernhard von Cotta in 1847 (lithograph) Carl Bernhard von Cotta, known as Bernhard von Cotta (24 October 1808 – 14 September 1879), was a German geologist. Life He was born in a forester's lodge at Kleine Zillbach, Meiningen, near Eisenach, the son of Heinrich von Cotta, founder of the Tharandt Forestry Academy near Dresden.[1] He was educated first at the Tharnadt Academcy, then at the Bergakademie Freiberg and the University of Heidelber...

Helen Cary RussellMrs. Dorian M. Russell (1924)BornHelen Ellen CaryAugust 6, 1870Newark, New York, U.S.DiedOctober 25, 1946Michigan, U.S.Other namesMrs. Dorian M. RussellOccupationsclubwomansocial leadermagazine editorKnown forpresident, Michigan State Federation of Women's ClubsNotable workeditor, Michigan Club Bulletin and the Michigan Federation Forum Helen Cary Russell (also known as Mrs. Dorian M. Russell; August 6, 1870 ā October 25, 1946) was an American clubwoman, social l...




![{\displaystyle Z=[N,N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b95ccb1cd91491af5f851d7a26cf59723faa757)













