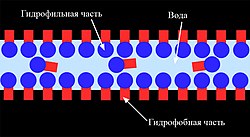
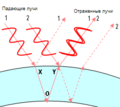
Мыльный пузырь
|
Read other articles:

Biru Gandaria Vinca majorCommon connotationsVinca Koordinat warnaTriplet hex#CCCCFFsRGBB (r, g, b)(204, 204, 255)HSV (h, s, v)(240°, 20%, 100%)SumberDaftar Istilah WarnaMaerz dan Paul[1]B: Dinormalkan ke [0–255] (bita) Biru gandaria adalah corak warna lembayung kebiruan yang alamiah ditemukan pada mahkota bunga dari tumbuhan Vinca.[2] Rujukan ^ Warna di atas sama dengan warna periwinkle dalam buku terbitan tahun 1930 ...

Republik AramoanaNegara mikro Bendera Lambang Semboyan: Let's save our territory(Indonesia: Mari selamatkan wilayah kita)Lagu kebangsaan: God defend Aramoana(Indonesia: Tuhan lindungilah Aramoana) Ibu kotaDunedin45°47′S 170°42′E / 45.783°S 170.700°E / -45.783; 170.700Koordinat: 45°47′S 170°42′E / 45.783°S 170.700°E / -45.783; 170.700Bahasa resmiInggrisDemonimAramoaniStruktur OrganisasiRepublik Presidensial• Presi...

Japan Academy PrizeDeskripsiKesempurnaan dalam pembuatan filmNegara JepangDipersembahkan olehAsosiasi Penghargaan Akademi JepangDiberikan perdana1978Situs webhttp://www.japan-academy-prize.jp/ Penghargaan Akademi Jepang (日本アカデミー賞code: ja is deprecated , Nippon Akademī-shō) adalah serangkaian penghargaan yang diberikan secara tahunan sejak 1978 oleh Nippon Academy-shō Association untuk kesempurnaan dalam film Jepang. Kategori penghargaannnya mirip dengan Academy Award. ...

Historic pub (now hotel) in Old Portsmouth, England Greyhound PubGeneral informationTypePublic houseCountryEngland The Greyhound was a pub (popularly known as The Spotted Dog), in High Street, Old Portsmouth, England. It is the site of the murder of George Villiers, 1st Duke of Buckingham in 1628. It is now a hotel. Architecture and conservation The building is timber-framed,[1] but this is not evident from outside as it has been refronted. It became a private building called Buckingh...

American politician and military officer For the American diplomat, see Henry Percival Dodge. For the American writer, see Henry Irving Dodge. Henry DodgePortrait of Dodge from the 1840sUnited States Senatorfrom WisconsinIn officeJune 8, 1848 – March 3, 1857Preceded bySeat establishedSucceeded byJames Rood DoolittleGovernor of the Wisconsin TerritoryIn officeApril 8, 1845 – June 23, 1848Appointed byJames PolkPreceded byNathaniel P. TallmadgeSucceeded byJohn Catlin (Actin...

2001 2017 Élections sénatoriales de 2011 en Nouvelle-Calédonie 25 septembre 2011 Type d’élection Élections sénatoriales Postes à élire 2 sièges de sénateur Pierre Frogier – R-UMP Voix au 1er tour 230 45,91 % Voix au 2e tour 240 47,90 % Hilarion Vendégou – R-UMP Voix au 1er tour 232 46,31 % Voix au 2e tour 238 47,50 % Charles Pidjot – UC Voix au 1er tour 117 23,35 % Voix au 2e tour 112 22,3...

Janusz KamińskiJanusz Kamiński tahun 2014LahirJanusz Zygmunt Kamiński27 Juni 1959 (umur 64)Ziębice, PolandiaKebangsaanPolandia[1]AlmamaterColumbia College Chicago (B.A., 1987)[2]Konservatori Lembaga Film Amerika (M.F.A., 1987)[3]PekerjaanSinematografer, sutradara film dan televisiTahun aktif1986–sekarangOrganisasiLembaga Film AmerikaPerhimpunan Sinematografer AmerikaSuami/istriHolly Hunter (m. 1995; c. 2001)...
Moses Malone Moses Malone nel 2005 Nazionalità Stati Uniti Altezza 208 cm Peso 118 kg Pallacanestro Ruolo Centro / Ala grandeAllenatore Termine carriera 1995 - giocatore2009 - allenatore Hall of fame Naismith Hall of Fame (2001) Carriera Giovanili Petersburg High School Squadre di club 1974-1975 Utah Stars83 (1.557)1975-1976 Spirits of St. Louis43 (614)1976 Buffalo Braves2 (0)1976-1982 Houston Rockets464 (11.119)1982-1986 Philadelphia 76ers302 (7.217)1986...

Canadian musician (born 1949) For the United States military aide to Iran, see Paul R. Shaffer. For the French holocaust survivor, see Paul Schaffer. For the Chilean cult leader, see Paul Schäfer. Paul ShafferCMShaffer in 2000BornPaul Allen Wood Shaffer (1949-11-28) November 28, 1949 (age 74)Toronto, Ontario, Canada[1]Occupation(s)Bandleader, musician, composer, actor, author, comedianYears active1972–presentSpouse Cathy Vasapoli (m. 1990)Ch...

Position des mains sur le clavier d'un piano. Glenn Gould disait : « La technique du piano est en vérité très simple, mais il faut des années pour la maîtriser ». Technique physique du piano Position du corps face à l'instrument Les observateurs attentifs des gravures, peintures, photographies et vidéo de pianistes célèbres seront surpris de constater à quel point la position des pianistes face à leur clavier est variée. Franz Liszt nous paraît dominer son clavie...

Lido AdrianofrazioneLido Adriano – Veduta LocalizzazioneStato Italia Regione Emilia-Romagna Provincia Ravenna Comune Ravenna TerritorioCoordinate44°24′49.68″N 12°18′29.88″E / 44.4138°N 12.3083°E44.4138; 12.3083 (Lido Adriano)Coordinate: 44°24′49.68″N 12°18′29.88″E / 44.4138°N 12.3083°E44.4138; 12.3083 (Lido Adriano) Abitanti7 000 (2015) Altre informazioniPrefisso0544 Fuso orarioUTC+1 TargaRA CartografiaL...

Sacred hymns of Zarathushtra This article is about the sacred hymns of Zarathushtra. For the Sanskrit and Prakrit verses, see Gatha. GathaInformationReligionZoroastrianismAuthorZarathustraLanguageAvestan Part of a series onZoroastrianism Primary topics Ahura Mazda Zarathustra Asha Vohu Manah Persia/Iran Faravahar Avestan Divine entities Amesha Spentas Yazatas Ahuras Daevas Fravashi Angra Mainyu Scripture and worship Avesta Ashem Vohu Ahuna Vairya Yenghe hatam Airyaman ishya Fire Temples 101 N...

Book of Psalms, chapter 51 This article is about the penitential psalm. For the musical settings based on the psalm, see Miserere (disambiguation) § Music. This article is about Psalm 51 in Hebrew (Masoretic) numbering. For Psalm 51 in Greek Septuagint or Latin Vulgate numbering, see Psalm 52. Psalm 51Have mercy upon me, O GodPenitential PsalmLatin text on a holy water font: see verse 9 belowOther name Psalm 50 Miserere mei, Deus LanguageHebrew (original) Psalm 51, one of the penitentia...

Ej att förväxla med Dominica. Dominikanska republikenRepública Dominicana Flagga Statsvapen Valspråk: Dios, patria, libertad (Spanska: Gud, fosterlandet, friheten) Nationalsång: Quisqueyanos valientes läge Huvudstad(även största stad) Santo Domingo Officiellt språk Spanska Demonym Dominikan Statsskick republik - President Luis Abinader - Vicepresident Raquel Peña Självständighet från Haiti - Erkänd 27 februari 1844 A...

This is a list of primary schools in Northern Ireland in which education is primarily conducted in Irish. There are 39 listed below and in each of the 6 counties, in descending order, there are: 11 in Antrim (Antroim), with 9 in Belfast (Béal Feriste) alone, 10 in Tyrone (Tír Eoghan), 8 in Londonderry (Doire ), 5 in Down (An Dún) 4 in Armagh (Ard Mhaca) 1 in Fermanagh (Fear Manach). Antrim Bunscoil an Chaistil, Ballycastle Gaelscoil Ghleann Darach, Crumlin Armagh Bunscoil Ard Mhacha Bunsc...

Penyuntingan Artikel oleh pengguna baru atau anonim untuk saat ini tidak diizinkan.Lihat kebijakan pelindungan dan log pelindungan untuk informasi selengkapnya. Jika Anda tidak dapat menyunting Artikel ini dan Anda ingin melakukannya, Anda dapat memohon permintaan penyuntingan, diskusikan perubahan yang ingin dilakukan di halaman pembicaraan, memohon untuk melepaskan pelindungan, masuk, atau buatlah sebuah akun. Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon...

Johann Friedrich Reichardt. Johann Friedrich Reichardt (1752-1814) adalah seorang musisi dan komponis berkebangsaan Jerman.[1] Ayah Reichardt adalah seorang musisi, dan dari ayahnya ia mendapat pelatihann dan pengetahuan dasar mengenai musik.[2] Di Universitas Koningsberg, Reichardt mempelajari piano, violin, dan komposisi musik, serta filsafat dan literatur.[2] Pada tahun 1771 hingga 1774, Reichardt mengembara, dan mengunjungi pusat musik di penjuru Austria dan Jerman...

American politician (born 1986) Lauren BoebertOfficial portrait, 2020Member of the U.S. House of Representativesfrom Colorado's 3rd districtIncumbentAssumed office January 3, 2021Preceded byScott Tipton Personal detailsBornLauren Opal Roberts (1986-12-19) December 19, 1986 (age 37)Altamonte Springs, Florida, U.S.Political partyRepublican (since 2008)Other politicalaffiliationsDemocratic (2006–2008)Spouse Jayson Boebert (m. 2007; div.&...

Untuk penerbang Amerika pada masa Perang Dunia I, lihat David Putnam. Untuk pemain sepak bola, lihat Dave Puttnam. The Right HonourableThe Lord PuttnamCBE HonFRSA HonFRPS MRIAPuttnam dalam acara British Academy Film Awards yang diadakan di Royal Opera House, London, pada Februari 2007LahirDavid Terence Puttnam25 Februari 1941 (umur 83)Southgate, London, InggrisPekerjaanProduser film dan pengajarSuami/istriPatricia Mary Jones (1961–sekarang)AnakAlexander (Sacha) Puttnam Deborah Jane Gro...

Nukleosintesis adalah proses penciptaan inti-inti atom baru dari nukleon-nukleon (proton dan neutron) yang sudah ada sebelumnya. Diduga bahwa nukleon-nukleon primordial sendiri terbentuk dari plasma kuark-gluon dari Big Bang (Dentuman Besar) ketika ia mendingin di bawah dua triliun Kelvin. Beberapa menit kemudian, bermula hanya dengan proton dan neutron, terbentuklah inti-inti aton sampai litium dan berilium (kedua-duanya berbilangan massa 7), tetapi hanya berjumlah relatif kecil. Kemudian pr...