Кривая роста (спектроскопия)
|
Read other articles:

Cinderella ManPoster promosi untuk Cinderella ManGenreRomansa DramaDitulis olehJo Yoon-yeongSutradaraYeo Jeong-joonPemeranKwon Sang-wooIm YoonaHan Eun-jungSong Chang-euiNegara asalKorea SelatanBahasa asliKoreaJmlh. episode16ProduksiLokasi produksiKoreaDurasiRabu dan Kamis pukul 21:55Rilis asliJaringanMunhwa Broadcasting CorporationRilis15 April (2009-04-15) –4 Juni 2009 (2009-6-4) Korean nameHangul신데렐라 맨 Alih AksaraSinderella MaenMcCune–ReischauerSinderella Maen ...

Winston DukeWinston Duke di San Diego Comic-Con tahun 2017Lahir15 November 1986 (umur 37)Argyle, TobagoPendidikanUniversitas Buffalo (BA)Universitas Yale (MFA)PekerjaanAktorTahun aktif2014–sekarang Winston Duke (lahir 15 November 1986) merupakan seorang aktor Trinidad dan Tobago. Ia dikenal sebagai aktor dalam film Marvel Cinematic Universe Black Panther (2018), Avengers: Infinity War (2018) dan Avengers: Endgame (2019). Ia dikenal sebagai aktor dalam film Us (2019). Latar belaka...

Krísti Stassinopoúlou Données clés Nom de naissance Chrysavyí Stassinopoúlou Naissance 20 janvier 1956 (68 ans)Athènes, Grèce modifier Chrysavyí Stassinopoúlou (grec moderne : Χρυσαυγή Στασινοπούλου), plus connue sous le nom de Krísti Stassinopoúlou (Κρίστη Στασινοπούλου), née le 20 janvier 1956 à Athènes, est une chanteuse grecque. Biographie Elle commence sa carrière en 1978 et interprète le rôle de Marie-Madeleine dans la...

Football rivalry in Scotland Angus DerbyLocationAngus, ScotlandTeamsArbroathMontroseForfar AthleticBrechin CityFirst meeting3 October 1885Arbroath 9–1 Forfar Athletic1885–86 Scottish Cup 2nd roundLatest meeting29 July 2023Arbroath 3–0 Montrose2023–24 Scottish League Cup group stageStatisticsMeetings total867 (As of 29 July 2023)Most winsForfar Athletic (185)All-time recordForfar Athletic (185)Arbroath (170)Brechin City (156)Montrose (151)Draw (204)Gayfield ParkLinks ParkStation ParkGl...

Voce principale: Unione Sportiva Grosseto Football Club. Unione Sportiva Grosseto Football ClubStagione 2006-2007Sport calcio Squadra Grosseto Allenatore Massimiliano Allegri poi Antonello Cuccureddu Presidente Piero Camilli Serie C11º posto (Promosso in Serie B) Coppa ItaliaPrimo turno Coppa Italia Serie COttavi Maggiori presenzeCampionato: Zizzari (32) Miglior marcatoreCampionato: Cipolla (12)Totale: Cipolla (15) StadioStadio Carlo Zecchini 2005-2006 2007-2008 Si invita a seguire il ...

American Revolutionary War soldier and politician (1735/36–1802) Daniel MorganMember of the U.S. House of Representativesfrom Virginia's 1st districtIn officeMarch 4, 1797 – March 3, 1799Preceded byRobert RutherfordSucceeded byRobert Page Personal detailsBorn1735 (1735) or 1736 (1736)Hunterdon County, Province of New Jersey, British AmericaDiedJuly 6, 1802 (aged 65–67)Winchester, Virginia, U.S.Resting placeMount Hebron Cemetery, Winchester, VirginiaPolitical p...

Universitas BondMotoForever LearningJenisPrivat, tidak untuk profitDidirikan1987KanselirDr. Helen Nugent AO[1]Wakil KanselirProfessor Tim BrailsfordSarjanasekitar 2,900 pelajarMagistersekitar 1,200 pelajarLokasiRobina, Gold Coast, Queensland, AustraliaSitus webwww.Bond.edu.au Universitas Bond adalah universitas tidak untuk profit privat yang berlokasi di Robina, Gold Coast, Queensland, Australia. Wakil rektor Don Watts (1987–1990) Philip Lader (1991–1993) Harry Messel (1993�...

Numismatic Guaranty CompanyJenisTertutupIndustriNumismatikDidirikan1987, Parsippany, New JerseyKantorpusatSarasota, FloridaWilayah operasiSeluruh duniaJasaSertifikasi KoinIndukCertified Collectibles GroupSitus webwww.ngccoin.com Numismatic Guaranty Company sebelumnya disebut Numismatic Guaranty Corporation atau biasa disingkat (NGC)[1] adalah sebuah perusahaan jasa layanan sertifikasi koin internasional yang berbasis di Sarasota, Florida, Amerika Serikat. Hingga saat ini NGC telah men...

Upper house of the Oireachtas (Irish parliament) Seanad Éireann26th SeanadTypeTypeUpper house of the Oireachtas HistoryEstablished29 December 1937 (Modern form)Preceded byIrish Free State SeanadNew session started29 June 2020LeadershipCathaoirleachJerry Buttimer, FG since 16 December 2022 Leas-ChathaoirleachMark Daly, FF since 16 December 2022 Leader of the SeanadLisa Chambers, FF since 16 December 2022 Deputy leaderRegina Doherty, FG since 16 December 2022 Opposition le...

Нотариа́т — общественный институт, занимающийся удостоверением сделок и приданием юридической силы различным документам (завещаниям, доверенностям, копиям документов и т. д.). Содержание 1 Виды нотариата 1.1 Нотариат латинского типа 1.1.1 Международный союз латинс�...

Appointments by King George V The 1915 Birthday Honours were appointments by King George V to various orders and honours to reward and highlight good works by citizens of the British Empire. The appointments were made to celebrate the official birthday of The King, and were published in The London Gazette[1] and in The Times on 3 June 1915.[2] Many of the honours were awarded for efforts in the war. The Times noted, The lists of Honours conferred on the occasion of the King's ...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

Beato Luigi Biraghi Presbitero e fondatore NascitaVignate, 2 novembre 1801 MorteMilano, 11 agosto 1879 (77 anni) Venerato daChiesa cattolica BeatificazioneMilano, 30 aprile 2006 da papa Benedetto XVI Ricorrenza28 maggio[1] Manuale Luigi Biraghi (Vignate, 2 novembre 1801 – Milano, 11 agosto 1879) è stato un presbitero italiano. È stato beatificato nel 2006.[2] Indice 1 Biografia 2 Note 3 Bibliografia 4 Altri progetti 5 Collegamenti esterni Biografia Fu ordin...

Ini adalah nama Batak Toba, marganya adalah Sijabat. Jerome Polin SijabatInformasi pribadiLahirJerome Polin Sijabat2 Mei 1998 (umur 26)Jakarta, IndonesiaPendidikan KB & TK Taman Harapan Malang SD & SMP Intan Permata Hati Surabaya Barat SMA Negeri 5 Surabaya Universitas Waseda PekerjaanYouTubermahasiswapengusahaKerabatJehian Panangian Sijabat (Kakak)Situs webwww.mantappu.com/talent/jerome-polin-sijabat/Informasi YouTubeKanal Nihongo Mantappu LokasiIndonesiaJepangPembuatJerome Poli...

LeptinStructure of the obese protein leptin-E100.[1]IdentifiersSymbolLeptinPfamPF02024Pfam clanCL0053InterProIPR000065SCOP21ax8 / SCOPe / SUPFAMAvailable protein structures:Pfam structures / ECOD PDBRCSB PDB; PDBe; PDBjPDBsumstructure summaryPDB1ax8 Teleost leptins are a family of peptide hormones found in fish (teleostei) that are orthologs of the mammalian hormone leptin. The teleost and mammalian leptins appear to have similar functions, namely, regulation of ene...

Juan Gris, Nature morte à la nappe à carreaux (Still Life with Checkered Tablecloth), 1915, huile sur toile (116,5 × 89,3 cm), Metropolitan Museum of Art (le Met), New York. Le cubisme est un mouvement artistique du début du XXe siècle, qui constitue une révolution dans la peinture et la sculpture, et influence également l'architecture, la littérature et la musique. Produites essentiellement dans la région parisienne, les œuvres cubistes représentent des objets ...

2017 extended play by Gugudan Act. 2 NarcissusEP by GugudanReleasedFebruary 27, 2017 (2017-02-27)Recorded2016–2017GenreK-popLength20:27LanguageKoreanLabelJellyfishCJ E&MProducerMaria MarcusChowoolRaviPUFFGlory FaceJinliMELODESIGNGugudan chronology Act. 1 The Little Mermaid(2016) Act. 2 Narcissus(2017) Act. 3 Chococo Factory(2017) Singles from Act. 2 Narcissus A Girl Like MeReleased: February 27, 2017 (2017-02-27) Act. 2 Narcissus is the second extended ...

English economist (1899–1988) For other people with the same name, see William Hutt (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: William Harold Hutt – news · n...

Charles River Link Trail Chase Woodlands is a nature reserve located in Dover, Massachusetts. The property was acquired by The Trustees of Reservations in 1993.[1] The reservation includes 2.5 miles of trails and is located across Farm Street from the Peters Reservation. The Charles River Link Trail crosses both reservations.[2] References ^ Chase Woodlands. The Trustees of Reservations. Retrieved May 15, 2021. ^ Charles River Link Trail. Town of Wellesley. Retrieved 7 July 20...
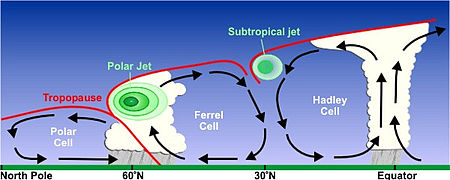
The boundary of the atmosphere between the troposphere and stratosphere This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Tropopause – news · newspapers · books · scholar · JSTOR (March 2012) (Learn how and when to remove this message) The tropopause extends to high altitudes in the tropical latitudes and exte...































![{\displaystyle W={\frac {2g}{\sqrt {\ln 2}}}\int _{0}^{\infty }\left(1-\exp \left[-\tau _{0}e^{-u^{2}}\right]\right)du}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b8e2ef5307c07497c0c230ecf4d258de4bab694)








![{\displaystyle W=2l\int _{0}^{\infty }\left(1-\exp \left[-{\frac {\tau _{0}}{y^{2}+1}}\right]\right)dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30b5250275b95365736a29622e63b2fd59a69bd7)

![{\displaystyle W=2l\int _{0}^{\infty }\left(1-\exp \left[-{\frac {\tau _{0}}{y^{2}}}\right]\right)dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0f9698ce748cf95db4fd92f502853cf77896518)

![{\displaystyle W=2l{\sqrt {\tau _{0}}}\int _{0}^{\infty }\left(1-\exp \left[-z^{2}\right]\right)d(1/z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e19a9a89fae400b341e0825e81522aae7cc80543)


