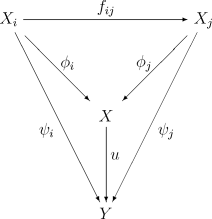
Индуктивный предел
|
Read other articles:

Untuk nama zaman di Jepang (1324-1325), lihat Shōchū (nama zaman) ShōchūJenisMinuman keras dan soju & shōchū (en) AsalJepang Komposisiberas, barley (en) dan Sweet potato (en) [sunting di Wikidata]lbs Shochu (焼酎code: ja is deprecated , Shōchū) adalah sebutan untuk minuman keras asal Jepang yang kandungan alkoholnya lebih tinggi dari sake atau anggur, tetapi lebih rendah dari wiski. Rasa dan aroma shochu sangat berbeda dari sake yang dibuat dari beras, karena bahan baku shoc...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Mobil SUV – berita · surat kabar · buku · cendekiawan · JSTOR Ford Escape Mercedes-Benz Kelas GLS Kendaraan Utilitas Sport (Bahasa Inggris: sport utility vehicle), disingkat SUV atau dijuluki Bemo adalah klas...

Janedjri M. Gaffar Sekretaris Jenderal Mahkamah Konstitusi RIMasa jabatan2004–2015PresidenSusilo Bambang YudhoyonoJoko Widodo Informasi pribadiLahir25 Oktober 1963 (umur 60) Yogyakarta, IndonesiaKebangsaan IndonesiaSuami/istriTetty ZainiartiAnakIntan Ajrina QadryaDwiki Syahbana PutraAlma materUniversitas Sebelas MaretSunting kotak info • L • B Janedjri M. Gaffar (lahir 25 Oktober 1963) adalah seorang pegawai negeri sipil yang menjabat Sekretaris Jenderal Mahkamah Kon...

Polish coat of arms CieleskiFamilies1 names Cieleski Cieleski is a Polish coat of arms. It was used by several szlachta families in the times of the Polish–Lithuanian Commonwealth. A variation of the Trestka coat of arms. History This section is empty. You can help by adding to it. (July 2010) Blazon This section is empty. You can help by adding to it. (July 2010) Notable bearers Notable bearers of this coat of arms include: See also Polish heraldry Heraldic family List of Polish nobility c...

Biarritzcomune Biarritz – VedutaPanorama LocalizzazioneStato Francia Regione Nuova Aquitania Dipartimento Pirenei Atlantici ArrondissementBayonne CantoneBiarritz AmministrazioneSindacoMichel Veunac (MoDem) dal 2014 TerritorioCoordinate43°29′N 1°34′W / 43.483333°N 1.566667°W43.483333; -1.566667 (Biarritz)Coordinate: 43°29′N 1°34′W / 43.483333°N 1.566667°W43.483333; -1.566667 (Biarritz) Altitudine0 - 85 m ...

Prefektur Vientiane Konurbasi Tempat <mapframe>: Judul Laos/Vientiane Prefecture.map .map bukan merupakan halaman data peta yang sah Negara berdaulatLaos NegaraLaos Pembagian administratifChanthabuly (en) Sikhottabong District (en) Xaysettha (en) Sisattanak District (en) Naxaithong (en) Xaythany (en) Hātsāifǭng (en) Sangthǭng (en) Pākngư̄m (en) GeografiLuas wilayah3.920 km² [convert: unit tak dikenal]Berbatasan denganProvinsi Vientiane Informasi tambahanZona waktuUTC+7 ISO ...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

American TV series or program Hairspray Live!Promotional posterGenreMusicalRomantic comedyLive televisionBased onHairspray (film)by John Waters Hairspray (musical)by Mark O'Donnelland Thomas Meehan Written byHarvey FiersteinDirected by Kenny Leon Alex Rudzinski Presented byDarren CrissStarring Maddie Baillio Harvey Fierstein Kristin Chenoweth Garrett Clayton Ariana Grande Jennifer Hudson Dove Cameron Ephraim Sykes Derek Hough Martin Short Shahadi Wright Joseph Composers Marc Shaiman Scott Wi...

Peta La Algaba (2002). La Algaba merupakan sebuah kota yang terletak di wilayah Provinsi Sevilla, Andalusia, Spanyol Lihat juga Daftar munisipalitas di Seville Daftar munisipalitas di Spanyol lbsKota di Provinsi Sevilla Aguadulce Alanís Albaida del Aljarafe Alcalá de Guadaíra Alcalá del Río Alcolea del Río Algámitas Almadén de la Plata Almensilla Arahal Aznalcázar Aznalcóllar Badolatosa Benacazón Bollullos de la Mitación Bormujos Brenes Burguillos Camas Cantillana Carmona Carrión...

American mathematician (1924–2021) Not to be confused with Isidore Singer. Isadore SingerSinger in 1977BornMay 3, 1924Detroit, Michigan, USDiedFebruary 11, 2021(2021-02-11) (aged 96)Boxborough, Massachusetts, USAlma materUniversity of MichiganUniversity of ChicagoKnown for Ambrose–Singer theorem Atiyah–Singer index theorem Atiyah–Hitchin–Singer theorem Ray–Singer torsion Kadison–Singer problem Spouse Rosemary Singer (m. 1956)Awards B...

Jaime Fillol Nazionalità Cile Altezza 180 cm Peso 73 kg Tennis Termine carriera 1985 Carriera Singolare1 Vittorie/sconfitte 463-324 Titoli vinti 7 Miglior ranking 14º (2 marzo 1974) Risultati nei tornei del Grande Slam Australian Open - Roland Garros 4T (1970, 1974, 1975, 1976) Wimbledon 4T (1974) US Open QF (1975) Doppio1 Vittorie/sconfitte 360-295 Titoli vinti 15 Miglior ranking 23º (22 maggio 1978) Risultati nei tornei del Grande Slam Australian Open...

VrauxcomuneVraux – Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementChâlons-en-Champagne CantoneChâlons-en-Champagne-2 TerritorioCoordinate49°01′N 4°14′E / 49.016667°N 4.233333°E49.016667; 4.233333 (Vraux)Coordinate: 49°01′N 4°14′E / 49.016667°N 4.233333°E49.016667; 4.233333 (Vraux) Superficie12,65 km² Abitanti486[1] (2009) Densità38,42 ab./km² Altre informazioniCod. postale51...

Questa voce sugli argomenti militari iracheni e criminali è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Abu al Hasan al Hashimi al Qurashi 3º Califfo dello Stato Islamico di Iraq e SiriaDurata mandato10 marzo 2022 –14 ottobre 2022 PredecessoreAbu Ibrahim al-Hashimi al-Qurayshi SuccessoreAbu al-Hussein al-Husseini al-Qurashi Dati generaliSuffisso onorificoCaliffo ProfessioneTerro...

穆罕默德·达乌德汗سردار محمد داود خان 阿富汗共和國第1任總統任期1973年7月17日—1978年4月28日前任穆罕默德·查希爾·沙阿(阿富汗國王)继任穆罕默德·塔拉基(阿富汗民主共和國革命委員會主席團主席) 阿富汗王國首相任期1953年9月7日—1963年3月10日君主穆罕默德·查希爾·沙阿 个人资料出生(1909-07-18)1909年7月18日 阿富汗王國喀布尔逝世1978年4月28日(...

Private university in Tusculum, Tennessee, U.S. A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (September 2017) (Learn how and when to remove this message) Tusculum UniversityFormer namesGreeneville College (1794–1868)Tusculum Academy (1818–1844)Tusculum College (1844–1868)Greeneville & Tusculum Col...

Japanese politician (born 1953) The native form of this personal name is Okada Katsuya. This article uses Western name order when mentioning individuals. Katsuya Okada岡田 克也Okada in 2023President of the Democratic Party of JapanIn office14 December 2014 – 1 October 2016Preceded byBanri KaiedaSucceeded byRenhōIn office18 August 2004 – 17 September 2005Preceded byNaoto KanSucceeded bySeiji MaeharaDeputy Prime Minister of JapanIn office13 January 2012 –&#...

Russian businessman (1954–2022) In this name that follows Eastern Slavic naming customs, the patronymic is Ulfatovich and the family name is Maganov. You can help expand this article with text translated from the corresponding article in Russian. (March 2024) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the transl...

Main article: Rowing at the 2019 Pan American Games This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Rowing at the 2019 Pan American Games – Qualification – news · newspapers · books · scholar · JSTOR (September 2020) (Learn how and when to remove this message) Rowing at the2019 Pan American GamesQualifica...

Species of fish Cole's char Conservation status Near Threatened (IUCN 3.1)[1] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Salmoniformes Family: Salmonidae Genus: Salvelinus Species: S. colii Binomial name Salvelinus colii(Günther, 1863) Synonyms previous scientific names Salvelinus scharffi Regan, 1911[2]Salvelinus trevelyani Regan 1908, 1911[3] Salvelinus colii, also called Cole's char,[4&...

Questa voce sull'argomento missioni spaziali è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. STS-104Emblema missione Dati della missioneOperatoreNASA NSSDC ID2001-028A SCN26862 ShuttleAtlantis Lancio12 luglio 2001, 5:04 a.m. EDT Luogo lancioRampa 39B Atterraggio24 luglio 2001, 11:38 p.m EDT Sito atterraggioJohn F. Kennedy Space Center, Shuttle Landing Facility (pista 15) Durata12 giorni, 18 ore e 3...