Дифференциальная геометрия поверхностей
|
Read other articles:

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

India Utara India Utara (Dewanagari: उत्तर भारत, Uttar Bhārat; Urdu: شمالی ھندوستان, Shumālī Hindustān) adalah wilayah yang terletak di bagian utara India. Batas resmi wilayah ini tidak pasti. Ciri-ciri geografis utama di India Utara adalah Dataran Indus-Gangga dan Pegunungan Himalaya, yang membatasi wilayah ini dengan Tibet dan Asia Tengah. Sejarah mencatat, negara Maurya, Gupta, Mughal, Maratha, Sikh dan Kemaharajaan Britania pernah berdiri di India Utara....

American college soccer team Princeton Tigersmen's soccerFounded1869; 155 years ago (1869)UniversityPrinceton UniversityHead coachJim Barlow (20th season)ConferenceIvyLocationPrinceton, New JerseyStadiumRoberts Stadium (soccer stadium) (Capacity: 1,000)NicknameTigersColorsBlack and orange[1] Home Away Pre-tournament ISFA/ISFL championships1921, 1922, 1925, 1926, 1927, 1936, 1937, 1939, 1940NCAA Tournament College Cup1993NCAA Tournament Qua...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

2008 Single by Jay-Z and T.I. featuring Kanye West, Lil Wayne, and M.I.A. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Swagga Like Us – news · newspapers · books · scholar · JSTOR (July 2020) (Learn how and when to remove this template message) Swagga Like UsSingle by Jay-Z and T.I. featuring Kanye West a...

Argentine diplomat Elena HolmbergBornElena Angélica Dolores Holmberg Lanusse(1931-05-24)24 May 1931Buenos Aires, ArgentinaDisappeared20 December 1978 (aged 47)Buenos Aires, ArgentinaOccupationDiplomat Elena Angélica Dolores Holmberg Lanusse (24 May 1931 – disappeared 20 December 1978), better known as Elena Holmberg, was an Argentine diplomat who was kidnapped and assassinated in 1978. Distinguished for being the first woman to graduate from the Institute of Foreign Services of the N...

1920–1991 ruling party of Armenia This article is about the ruling Communist Party of Armenia during the Soviet era. For the post-Soviet Union communist party in the Republic of Armenia established in 1991, see Armenian Communist Party. Communist Party of Armenia Հայաստանի կոմունիստական կուսակցությունFirst SecretaryAram G. Sargsyan (last)Founded31 December 1920Dissolved7 September 1991Split fromUnion of Armenian Social DemocratsSucceeded byDemoc...

Low-cost airline of Indonesia Indonesia AirAsia IATA ICAO Callsign QZ AWQ WAGON AIR Founded1999; 25 years ago (1999)(as Awair)Commenced operations22 June 2000; 23 years ago (2000-06-22)(as Awair)1 December 2005; 18 years ago (2005-12-01)(as Indonesia AirAsia)Operating basesDenpasarJakarta–Soekarno-HattaLombokMedanSurabayaFrequent-flyer programBIG Loyalty ProgrammeFleet size32Destinations33Parent companyPT AirAsia Indonesia Tbk.Headquarte...

Pour les articles homonymes, voir Annie Get Your Gun. Annie Get Your Gun Betty Hutton dans Annie, la reine du cirque Données clés Titre original Annie Get Your Gun Réalisation George Sidney Scénario Sidney Sheldon Musique Irving BerlinRoger Edens (non crédité) Acteurs principaux Betty HuttonHoward Keel Sociétés de production Metro-Goldwyn-Mayer Pays de production États-Unis Genre westernbiographiquemusical Durée 107 minutes Sortie 1950 Pour plus de détails, voir Fiche technique et...

Verner von Heidenstam Portrait de Verner von Heidenstam par Johan Krouthén. Données clés Nom de naissance Carl Gustaf Verner von Heidenstam Naissance 6 juillet 1859 Olshammar, Comté d'Örebro Décès 20 mai 1940 (à 80 ans) Övralid, Comté d'Östergötland Activité principale Romancier, poète, essayiste Distinctions Prix Nobel de littérature en 1916 Auteur Langue d’écriture Suédois Mouvement Fin-de-siècle en Suède modifier Carl Gustaf Verner von Heidenstam, né le 6 juille...

Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) Roche Tower – Switzerland's tallest building since 2015 Grande Dixence Dam, 285 m Blosenbergturm 217 m Hammetschwand Elevator, 157 m Basler Messeturm, 105 m Münster of Bern, 100 m A list of tallest structures in Switzerland. This list may be incomplete and incorrect. indicates a structure that is no longer standing...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Association football club in Bulgaria Football clubFC Vitosha BistritsaFull nameFootball Club Vitosha BistritsaNickname(s)The Bistritsa TigersShort nameVitoshaFounded1958; 66 years ago (1958)GroundStadion BistritsaCapacity2,500ManagerNikolay HristozovLeagueSouthwest Third League2022–23Second League, 17th (relegated)WebsiteClub website Home colours Away colours Third colours FC Vitosha (Bulgarian: ФК Витоша) is a Bulgarian association football club based in Bistrits...
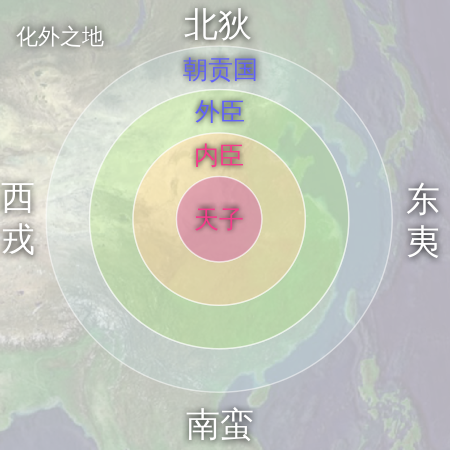
此條目需要补充更多来源。 (2015年4月28日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:南蠻 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 南蠻汉语名称繁体字 南蠻 简化字 南蛮 标音官话(現代標準漢語)- 汉语拼音 Ná...

The White Doe of Rylstone by John William Inchbold The White Doe of Rylstone; or, The Fate of the Nortons is a long narrative poem by William Wordsworth, written initially in 1807–08, but not finally revised and published until 1815. It is set during the Rising of the North in 1569 and combines historical and legendary subject-matter. It has attracted praise from some critics, but has never been one of Wordsworth's more popular poems. Synopsis The White Doe of Rylstone opens outside Bolton...

Untuk kegunaan lain, lihat Dr. Jekyll dan Tuan Hyde. Kasus Aneh Dr Jekylldan Tuan Hyde Halaman judul dari edisi pertama London (1886)PengarangRobert Louis StevensonNegaraBritania RayaBahasaInggrisPenerbitLongmans, Green & co.Tanggal terbit5 Januari 1886ISBNISBN N/A Invalid ISBN Kasus Aneh Dr Jekyll dan Tuan Hyde atau hanya Dr. Jekyll dan Tuan Hyde (judul aslinya Strange Case of Dr. Jekyll and Mr. Hyde) adalah novel yang ditulis oleh penulis Skotlandia Robert Louis Stevenson...

Artikel ini bukan mengenai Avīci. AviciiAvicii pada tahun 2014Informasi latar belakangNama lahirTim BerglingNama lainTim BergTim LidénTom HangsTimbermanLahir(1989-09-08)8 September 1989Stockholm, SwediaMeninggal20 April 2018(2018-04-20) (umur 28)Muscat, OmanGenre EDM progressive house electro house Pekerjaan Disjoki remixer produser rekaman Instrumen Gitar piano keyboard synthesizers Tahun aktif2006–2018Label Geffen[1] UMG Artis terkait David Guetta Wyclef Jean Coldplay Selen...

Hong Kong football player Adam Tse Adam Tse training with South China before the First Division match against Tuen Mun on 16 March 2013Personal informationFull name English: Adam Chi Keung TseTraditional Chinese: 謝志強Date of birth (1990-06-22) June 22, 1990 (age 34)[1]Place of birth Salford, EnglandHeight 1.79 m (5 ft 10 in)[1]Position(s) ForwardSenior career*Years Team Apps (Gls) Clifton Lighoaks Villa 2013 South China 4 (0) *Club domestic league appe...

Phyllanthaceae Breynia disticha Klasifikasi ilmiah Kerajaan: Plantae Klad: Angiospermae Klad: Eudikotil Klad: Rosid Klad: Rosid Ordo: Malpighiales Famili: PhyllanthaceaeMartynov[1] Genera Lihat teks Suku meniran-meniranan atau Phyllanthaceae adalah salah satu suku anggota tumbuhan berbunga. Menurut Sistem klasifikasi APG II suku ini dimasukkan ke dalam bangsa Malpighiales, klad euRosidae I. Suku ini dalam Sistem Cronquist merupakan anaksuku Phyllanthoideae dari suku kastuba-kastubaan...

Public university in Menomonie, Wisconsin, US University of Wisconsin–StoutFormer namesStout Manual Training School (1891–1908)Stout Institute (1908–1955)Stout State College (1955–1965)Stout State University (1965–1971)TypePublic universityEstablished1891Parent institutionUniversities of WisconsinEndowment$64,505,176 (2019)[1]ChancellorKatherine FrankAcademic staff482Students6,938 (fall 2023)Undergraduates6,080 (fall 2023)Postgraduates858 (fall 2023)LocationMenomonie, Wiscon...







