Дисторсия
|
Read other articles:

Daud dan Goliat: Ilustrasi Yahudi pada abad ke-13 asal Prancis. Goliat atau Jalut (Ibrani: גָּלְיָת, Golyat, Golyāṯ, Arab جالوت, Ǧālūt (istilah Al-Qur'an), جليات Ǧulyāt (istilah Kristen), Inggris Goliath) (meninggal ~ 1010 SM) adalah seorang prajurit Filistin, terkenal karena pertempurannya dengan Daud muda. Nama Goliat disebut dalam kitab Perjanjian Lama dan Al-Qur'an.[1] Tradisi Yahudi pasca-klasik menekankan bahwa tradisi Yahudi Goliat berstatus sebagai wa...

Universitas Borneo TarakanDidirikan9 Oktober 1999Lembaga indukKementerian Pendidikan, Kebudayaan, Riset, dan TeknologiRektorProf. Dr. Adri Patton, M.SiLokasiTarakan Gedung rektorat Universitas Borneo Tarakan Salah satu sudut di kampus Universitas Borneo Universitas Borneo Tarakan disingkat sebagai UBT adalah sebuah perguruan tinggi negeri yang berkedudukan di Kota Tarakan, Kalimantan Utara. Kampus utama Universitas Borneo, terletak di Jl. Amal Lama No.1 Tarakan. Universitas Borneo didirikan o...

British experimental music magazine Not to be confused with Wired (magazine) or The Wire (India). For other uses, see Wire (disambiguation). The WireFreedom PrinciplesThe Wire no. 370, Dec. 2014EditorDerek Walmsley; see timeline below for former editorsCategoriesMusic magazineFrequencyMonthlyPublisherTony HerringtonFounderAnthony Wood, Chrissie MurrayFirst issueSummer 1982 (1982)CompanyThe Wire Magazine Ltd. (independently owned)Based inLondon, EnglandLanguageEnglishWebsitethewire.c...

Island group is located in the Pyasina Bay, in the Kara Sea Location of the Zveroboy Islands in the Kara Sea. The Zveroboy Island group in the gulf of the Pyasina. The Zveroboy Islands (Russian: Остров Зверобой, or Ostrov Zveroboy) is a group consisting of a large island (Zveroboy Island) and a few scattered small islets. The main island is 17 km in length. It is covered with tundra vegetation and has a lake. This island group is located in the Pyasina Bay, in the Kara Sea,...

قرية مورافيا الإحداثيات 42°42′40″N 76°25′23″W / 42.7111°N 76.4231°W / 42.7111; -76.4231 [1] تاريخ التأسيس 1789 تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كايوغا خصائص جغرافية المساحة 4.466358 كيلومتر مربع4.466364 كيلومتر مربع (1 أبريل 2010) ارتفا...

العلاقات الليتوانية الميانمارية ليتوانيا ميانمار ليتوانيا ميانمار تعديل مصدري - تعديل العلاقات الليتوانية الميانمارية هي العلاقات الثنائية التي تجمع بين ليتوانيا وميانمار.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدول�...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Anumerta – berita · surat kabar · buku · cendekiawan · JSTOR Anumerta (serapan dari bahasa Sanskerta: अनु- (anu-, setelah) + मृत (mṛta, wafat)) adalah tindakan atau kegiatan yang terkait de...

Space suit technology demonstrator The Mark III suit worn by NASA geologist Dean Eppler during field testing at Meteor Crater near Winslow, Arizona, US The Mark III or MK III (H-1) is a NASA space suit technology demonstrator built by ILC Dover. While heavier than other suits (at 59 kilograms (130 lb), with a 15 kilograms (33 lb) Primary Life Support System backpack), the Mark III is more mobile, and is designed for a relatively high operating pressure.[1] The Mark III is a ...

Ice hockey at the 1952 Winter OlympicsJersey of Canada's 1952 Olympic Gold Medal team, the Edmonton MercurysTournament detailsHost country NorwayVenue(s)Jordal Amfi Arena, Dælenenga, Kadettangen, Marienlyst and LillestrømDates15–25 February 1952Teams9Final positionsChampions Canada (6th title)Runner-up United StatesThird place SwedenFourth place CzechoslovakiaTournament statisticsGames played37Goals scored335 (9.05 per game)Scorin...
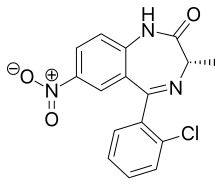
Chemical compound MeclonazepamClinical dataATC codenoneLegal statusLegal status CA: Schedule IV DE: NpSG (Industrial and scientific use only) UK: Under Psychoactive Substances Act Identifiers IUPAC name (3S)-5-(2-chlorophenyl)-3-methyl-7-nitro-1,3-dihydro-1,4-benzodiazepin-2-one CAS Number58662-84-3 NPubChem CID3033985ChemSpider2298544 YUNIIRN43209SMAChEMBLChEMBL351821 NCompTox Dashboard (EPA)DTXSID10207366 Chemical and physical dataFormulaC16H12ClN3O3Molar mass3...

Extinct genus of dinosaurs Not to be confused with Overoraptor. OviraptorTemporal range: Late Cretaceous,~75–71 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Holotype specimen of Oviraptor Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Clade: Dinosauria Clade: Saurischia Clade: Theropoda Family: †Oviraptoridae Subfamily: †Oviraptorinae Genus: †OviraptorOsborn, 1924 Type species †Oviraptor philoceratopsOsborn, 1924 Synonyms Fenestrosaurus philocerato...

Земская почтаУезды Алатырский Александрийский Ананьевский Ардатовский Арзамасский Аткарский Ахтырский Балашовский Бахмутский Бежецкий Белебеевский Белозерский Бердянский Бобровский Богородский Богучарский Борисоглебский Боровичский Бронницкий Бугульминский Бу�...

1992 Cholera outbreak Aerolíneas Argentinas Flight 386LV-MLR, the aircraft the event took place in.[citation needed]OccurrenceDate14 February 1992 (1992-02-14)SummaryMass foodborne illness outbreak by cholera from airline mealSiteIn flight from Lima, Perú to Los Angeles, United StatesAircraftAircraft typeBoeing 747-200BOperatorAerolíneas ArgentinasRegistrationLV-MLRFlight originMinistro Pistarini International Airport, Buenos Aires, ArgentinaLast stopoverJorge C...

Egyptian Coptic nun Maggie Gobran in 2019 Maggie Gobran (Arabic: ماجي جبران) or Mama Maggie, is a Coptic Orthodox consecrated servant and the founder and CEO of the non-profit charity Stephen's Children in Cairo, Egypt. She was also professor of computer science at the American University in Cairo, is married and has a son and a daughter.[1] She was nominated for Nobel Peace Prize in 2012 and 2020.[2][3] Life Maggie Gobran often referred to as the Mother Tere...

Type of legislative body This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: House of Assembly – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) Part of the Politics seriesPolitics Outline Index Category Primary topics Outline of political science Index of ...

Shooting at the 2022 Asian GamesVenueFuyang Yinhu Sports CentreDates24 September – 1 OctoberCompetitors675 from 36 nations← 20182026 → Shooting at the 2022 Asian Games was held in Fuyang Yinhu Sports Centre in Hangzhou, China between 24 September and 1 October 2023. Schedule ● 1st day ● Final day Q Qualification F Final Event↓/Date → 24thSun 25thMon 26thTue 27thWed 28thThu 29thFri 30thSat 1stSun Men's 10 m air pistol Q F Men's 10 m air pist...

American businessman and amateur ornithologist George Newbold LawrenceBorn(1806-10-20)October 20, 1806New York City, New York, U.S.DiedJanuary 17, 1895(1895-01-17) (aged 88)New York City, New York, U.S.Occupation(s)Businessman, ornithologist George Newbold Lawrence (October 20, 1806 – January 17, 1895) was an American businessman and amateur ornithologist.[1][2] Early life Lawrence was born in the city of New York on October 20, 1806.[1] From his youth, Lawrence...

Giada GallinaNazionalità Italia Altezza164 cm Peso54 kg Atletica leggera SpecialitàVelocità SocietàSnam Milano Record 60 m 764 (indoor – 1997) 100 m 1123 (1997) 200 m 2329 (1994) CarrieraNazionale 1992-1997 Italia17 Palmarès Competizione Ori Argenti Bronzi Europei juniores 0 1 0 Vedi maggiori dettagliStatistiche aggiornate al 1º ottobre 2011 Modifica dati su Wikidata · Manuale Giada Gallina (Montebelluna, 1º dicembre 1973) è un'ex velocista italiana, nove volte campio...

ツァーリ・コロコル ツァーリ・コロコルの位置 ツァーリ・コロコル(ロシア語: Царь–колокол、「鐘の皇帝」の意)は、ロシア・モスクワのクレムリン宮殿に展示されている巨大な鐘である。重量約160~200トン、高さ6.14メートル、直径6.60メートルである。 1733年から1735年にかけて、ロシア帝国の鋳造職人イワン・モトリンとその息子によって鋳造され、装飾や...

Representación esquemática del procedimiento legislativo del Congreso de los EE. UU. En los Estados Unidos, una ley del Congreso (en inglés Act of Congress) es una ley adoptada por el Congreso de los Estados Unidos. Ejemplo. Contenido Las leyes del Congreso de los Estados Unidos pueden tener contenido relativo al Derecho público (Public Law), si se refieren al público en general, o al Derecho privado (Private Law), si se refieren a instituciones o personas específicas. Desde 1957, todas...



![{\displaystyle \nu =\left[(b-b_{0})/b\right]\cdot 100\%,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dab7083b27b38c3e2e93a814ba8f83a8fa5a614)














