Выпуклая кривая
|
Read other articles:

Payung Hitam (Black Umbrella)SutradaraChairun NissaTanggal rilis2011Negara IndonesiaBahasaBahasa Indonesia Payung Hitam adalah sebuah film dokumenter karya sutradara Chairun Nissa. Film ini mendapatkan kesempatan untuk diputar di Salaya International Documentary Film Festival, Thailand, dan dan Flying Broom International Women's Film Festival di Turki.[1][2] Sinopsis Berkisah tentang perjuangan mencari keadilan dua orang perempuan, Neneng dan Sumarsih, yang bertemu dalam aksi ...

2004 Indian filmVarnajaalamDirected byNagulan PonnusamyWritten byNagulan PonnusamyProduced byV. Gnanavel,V. JayaprakashStarringSrikanthSadhaKutti RadhikaNassarRiyaz KhanKarunasCinematographyB. BalamuruganEdited byK. PalanivelMusic byVidyasagarProductioncompanyGJ CinemaRelease date 13 February 2004 (2004-02-13) CountryIndiaLanguageTamil Varnajalam is a 2004 Indian Tamil-language mystery thriller film written and directed by Nagulan Ponnusamy. The film stars Srikanth, Sadha, and...

FC EmmenNama lengkapFootball Club EmmenJulukanEmmenBerdiri21 Agustus 1925; 98 tahun lalu (1925-08-21)StadionStadion UnivéEmmen(Kapasitas: 8.600)ManajerGert HeerkesLigaEerste Divisie2011–12Eerste Divisie, peringkat 18 Kostum kandang Kostum tandang Stadion Univé di Emmen. Stadion Univé di Emmen. FC Emmen adalah sebuah klub sepak bola Belanda yang berbasis di Emmen, Drenthe, dan saat ini bermain di Eerste Divisie, tingkat kedua sepak bola di Belanda. Pemain saat ini Per 4 February 2021...

English naturalist and biologist (1809–1882) For other people named Charles Darwin, see Charles Darwin (disambiguation). Charles DarwinFRS FRGS FLS FZS JPDarwin, c. 1854, when he was preparing On the Origin of Species[4]BornCharles Robert Darwin(1809-02-12)12 February 1809Shrewsbury, EnglandDied19 April 1882(1882-04-19) (aged 73)Down, Kent, EnglandResting placeWestminster AbbeyAlma materUniversity of Edinburgh Christ's College, Cambridge (BA, 1831; MA, 1836...

2008 football riots in Manchester, England 2008 UEFA Cup final riotsPart of the history of Manchester and the 2007–08 UEFA CupOfficers of the Greater Manchester Police keep Rangers and Zenit fans apartDate14 May 2008LocationManchester City Centre,EnglandResult 39 policemen injured, one police-dog injured and 39 arrests[1]Belligerents Zenit hooligans Rangers hooligans Greater Manchester Police The 2008 UEFA Cup final riots were a series of public disorder incidents that took place in...

Pour les articles homonymes, voir Gore. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (octobre 2014). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique ...

Premio CésarLa statuetta di bronzo, simbolo del premio Luogo Parigi, Francia Anni1976 - ad oggi Fondato daAcadémie des arts et techniques du cinéma Dateinverno GenereCinema Sito ufficialewww.academie-cinema.org/ Modifica dati su Wikidata · Manuale Il premio César è un riconoscimento cinematografico assegnato annualmente dal 1976 dall'Académie des arts et techniques du cinéma ai migliori film e alle principali figure professionali del cinema francese. I premi sono assegnati al...

Komando Distrik Militer 1805/Raja AmpatLambang Korem 181/Praja Vira TamaDibentuk20 Agustus 2018Negara IndonesiaAliansiKorem 181/PVTCabangTNI Angkatan DaratTipe unitKodimPeranSatuan TeritorialBagian dariKodam XVIII/KSRMakodimRaja Ampat, Papua Barat DayaPelindungTentara Nasional IndonesiaMotoBekitem Beito Bematem WaneBaret H I J A U MaskotElang LautTokohKomandanLetkol Czi Tri Wibowo Komando Distrik Militer (disingkat Kodim) 1805/Raja Ampat merupakan salah satu Kodim di bawah jaja...

Untuk kegunaan lain The Telegraph, lihat The Telegraph (disambiguasi). Halaman depan The Daily Telegraph tanggal 12 Desember 2005TipeSurat kabar harianFormatTabloidPemilikNews LimitedRedaksiGary LinnellDidirikan1879Pandangan politikTengah-kananPusat2 Holt Street,Surry Hills, NSW, AustraliaSitus webwww.dailytelegraph.news.com.au The Daily Telegraph (sering disebut The Tele) adalah sebuah surat kabar tabloid Australia yang diterbitkan di Sydney, New South Wales dan negara NSW, oleh Nationwide N...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2015年7月23日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目內容疑欠准确,有待查證。 (2015年7月23日)請在讨论页討論問題所在及加以改善,若此條目仍有爭議及准确度欠佳,會被提出存廢討論。 此條目之中立性有�...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Céruse Blanc de céruse obtenu par oxydation de feuilles de plomb. Identification Synonymes C.I. pigment white 1 No CAS 1319-46-6 No ECHA 100.013.901 No CE 215-290-6 SMILES C([O-])([O-])=O.C(=O)([O-])[O-].[Pb+2].[Pb+2].[Pb+2].[OH-].[OH-] PubChem, vue 3D InChI InChI : vue 3D InChI=1/2CH2O3.2H2O.3Pb/c2*2-1(3)4;;;;;/h2*(H2,2,3,4);2*1H2;;;/q;;;;3*+2/p-6 Propriétés chimiques Formule C2H2O8Pb3(PbCO3)2·Pb(OH)2 Masse molaire[a] 775,6 ± 0,3 g/mol C 3,1 %, H...

Seorang pelayan kopi, dari wilayah Utsmaniyah di Kairo, Mesir pada tahun 1857. Sebuah rumah kopi di Damaskus. Sebuah Rumah kopi Wina Les Deux Magots di Paris, sempat menjadi tempat perkumpulan para intelektual Prancis yang terkenal Sebuah kafe kopi di Melbourne. Kota tersebut dikatakan memiliki beberapa kopi terbaik di dunia. Budaya kopi mendeskripsikan atmosfer sosial atau serangkaian perilaku sosial terkait yang sangat bergantung pada kopi, sebagian besar sebagai sebuah lubrikan sosial. Ist...

Form of primary legislation in Wales This article is about the lower form of legislation of the National Assembly for Wales between 1999 and 2011. For the higher form of primary legislation, known as Acts of the Assembly, and later of the Senedd from 2020, see Act of Senedd Cymru. The Royal Badge of Wales appears on Assembly Measures[1] A Measure of the National Assembly for Wales (informally, an Assembly Measure) is primary legislation in Wales that is a category lower than an Act of...

Parasitic disease due to invasion by Trichinella spp. This article is about the disease. For the parasite, see Trichinella. Not to be confused with Trichomoniasis or Trichuriasis. Medical conditionTrichinosisOther namesTrichinellosis, trichiniasisTrichinella larvae in pressed bear meat, partially digested with pepsin. The classic coil shape is visible.SpecialtyInfectious diseaseSymptomsInitially: diarrhea, abdominal pain, vomiting[1]Later: swelling of the face, inflammation of the whi...

SN 1987A dengan sisa cincin di sekitarnya. SN 1987A adalah supernova tipe II yang berjarak sekitar 168.000 tahun cahaya di Awan Magellan Besar. Ini signifikan secara ilmiah karena memberi peluang besar untuk mempelajari supernova runtuh-inti melalui fase sebelum, selama dan setelah kematian sebuah bintang.[1][2] Meskipun ledakan bintang terjadi sekitar 166.000 SM, cahaya dari SN 1987A pertama kali terlihat pada 23 Februari 1987. Gelombang kejut yang sangat terang dari ledakan ...

This article is part of a series aboutDonald Trump Business and personal Business career The Trump Organization wealth tax returns Media career The Apprentice bibliography filmography Eponyms Family Foundation American football Golf Honors Public image in popular culture SNL parodies handshakes Legal affairs Sexual misconduct allegations Nicknames pseudonyms Racial views Comments on John McCain Conspiracy theories Residences Rhetoric 45th President of the United States Presidency timeline Tr...
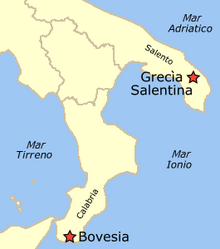
Questa voce o sezione sull'argomento linguistica è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. GrecanicoGrecanicoParlato in Italia R...

Cet article est une ébauche concernant une catastrophe aérienne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Vol National Airlines 27 N60NA, l'appareil impliqué, ici en octobre 1974, 1 an après l'incident. Caractéristiques de l'accident Date3 novembre 1973 TypeDécompression explosive CausesDéfaillance non-contenue d'un moteur en vol SiteAu dessus de Socorro, au Nouveau-Mexique, aux États-Unis Coordon...

Miss Madeline comment Yes, I saw you comment on Miss Madeline's talk page and yes things have been great expect for the EPAC stuff. Will you try and straiting a little when you have a chance bat least let me know if you are for or againsted on my talk page we are spit even about this. We are still doing great, though. Well i need to return to my wikibreak. Cheers. Leave Message ,Yellow Evan home ,Sandbox[ 02:02, 2 November 2008 (UTC)[reply] I saw you comment on Miss Madeline's talk page abou...


