Вращение
|
Read other articles:

العلاقات السورية الكرواتية سوريا كرواتيا سوريا كرواتيا تعديل مصدري - تعديل العلاقات السورية الكرواتية هي العلاقات الثنائية التي تجمع بين سوريا وكرواتيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارنة سور�...

منتخب جزر سليمان لكرة القدم معلومات عامة بلد الرياضة جزر سليمان الفئة كرة القدم للرجال رمز الفيفا SOL الاتحاد اتحاد جزر سليمان لكرة القدم كونفدرالية أوفك (أوقيانوسيا) الملعب الرئيسي ملعب لاوسون تاما الموقع الرسمي الموقع الرسمي الطاقم واللاعبون المدرب فيليبي �...

إراكليا تقسيم إداري البلد اليونان [1] خصائص جغرافية إحداثيات 41°10′59″N 23°16′55″E / 41.18305556°N 23.28194444°E / 41.18305556; 23.28194444 المساحة 14.345 كيلومتر مربع[2] الارتفاع 38 متر السكان التعداد السكاني 3245 (resident population of Greece) (2021)3584 (resident population of Greece) (2001)3874 (resident pop...

Phoenix Raceway Anciens noms Phoenix International Raceway (1964-2014, 2016-2017) Jeff Gordon Raceway (2015) Phoenix Raceway (2017, depuis 2020) ISM Raceway (2018-2020) Caractéristiques générales Lieu 7602 S Avondale BoulevardAvondale, Arizona 85323 États-Unis Coordonnées 33° 22′ 29″ nord, 112° 18′ 40″ ouest Géolocalisation sur la carte : Arizona localisation Géolocalisation sur la carte : États-Unis localisation Construction 1964 Pro...

Andrus Ansip Andrus Ansip en 2017. Fonctions Député européen En fonction depuis le 2 juillet 2019(4 ans et 10 mois) Élection 26 mai 2019 Législature 9e Groupe politique RE 1er juillet – 31 octobre 2014(3 mois et 30 jours) Élection 25 mai 2014 Législature 8e Groupe politique ADLE Vice-président de la Commission européenneChargé du Marché numérique unique 1er novembre 2014 – 1er juillet 2019(4 ans et 8 mois) Président Jean-Claude Juncker Gouvernem...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

2009 single by Taylor Swift This article is about the Taylor Swift song. For other uses, see 15 (disambiguation) § Songs. FifteenSingle by Taylor Swiftfrom the album Fearless ReleasedAugust 31, 2009 (2009-08-31)Recorded2008StudioBlackbird (Nashville)Genre Country pop guitar pop Length4:55LabelBig MachineSongwriter(s)Taylor SwiftProducer(s) Taylor Swift Nathan Chapman Taylor Swift singles chronology You Belong with Me (2009) Fifteen (2009) Two Is Better Than One (2009) Mus...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. SMK Tunas Harapan PatiInformasiDidirikan1990Kepala SekolahIr. Eny WahyuningsihAlamatLokasi, Kabupaten Pati, Jawa Tengah, IndonesiaMoto SMK Tunas Harapan Pati adalah sebuah sekolah yang terletak di Kabupaten Pati, provinsi Jawa Tengah, Indonesia. Sej...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...
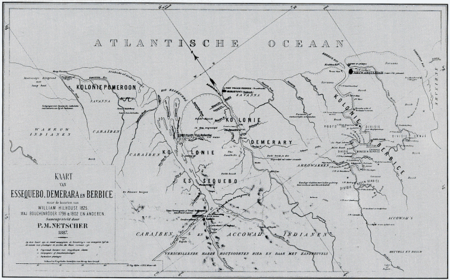
Cet article est une ébauche concernant le Guyana. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Carte des colonies néerlandaises de la Côte Sauvage (Amérique du Sud) autour de 1800. De gauche à droite : Pomeroon, Essequibo, Démérara et Berbice. Berbice (/bɛʁ.bis/) était une ancienne colonie néerlandaise située le long du fleuve Berbice sur la Côte Sauvage sud-américaine, dans l'actuel Guyana...
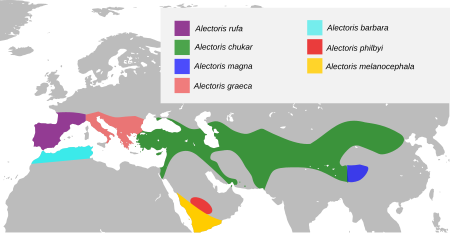
ميّز عن شنار. اضغط هنا للاطلاع على كيفية قراءة التصنيف حجل شقر حالة الحفظ أنواع غير مهددة أو خطر انقراض ضعيف جدا (IUCN 3.1)[1] المرتبة التصنيفية نوع[2][3] التصنيف العلمي المملكة: الحيوانية الشعبة: حبليات الطائفة: الطيور الرتبة: دجاجيات الفصيلة: تدرجية الجن...

Selusur maninjau Homaloptera gymnogaster TaksonomiKerajaanAnimaliaFilumChordataKelasActinopteriOrdoCypriniformesFamiliBalitoridaeGenusHomalopteraSpesiesHomaloptera gymnogaster Bleeker, 1853 lbs Homalopterula gymnogaster atau selusur maninjau adalah spesies ikan bersirip pari dalam genus Homalopterula . Ia biasa dijumpai di tasik air tawar Maninjau di Sumatera Barat, Indonesia. Referensi

County in Vermont, United States County in VermontOrleans CountyCountyOrleans County Courthouse in Newport (city)Location within the U.S. state of VermontVermont's location within the U.S.Coordinates: 44°50′40″N 72°13′06″W / 44.844402°N 72.218239°W / 44.844402; -72.218239Country United StatesState VermontFounded1799Named forOrléans, FranceShire TownNewportLargest cityDerbyArea • Total721 sq mi (1,870 km2) • ...

Belgian pharmaceutical research company Galapagos NVFormerlyGalapagos Genomics NVCompany typeNaamloze vennootschapTraded asEuronext Amsterdam: GLPGBEL 20 componentISINBE0003818359IndustryPharmaceuticalFounded1999HeadquartersMechelen, BelgiumKey peoplePaul Stoffels (CEO)Raj Parekh (Chairman)ProductsFilgotinib; GLPG1205; GLPG0778Revenue€288.836 million (2018)[1]Net income€-29.259 million (2018)[1]Total assets€1,439.496 million (2018)[1]Total equity€1,214.249...

Kylian KaïbouéNazionalità Francia Altezza179 cm Peso65 kg Calcio RuoloDifensore, centrocampista Società Amiens CarrieraGiovanili 2005-2018 Montpellier Squadre di club1 2015-2020 Montpellier 269 (10)2020-2021→ Sète27 (1)2021-2023 Bastia61 (3)2023- Amiens23 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Statistiche aggiornate al 26 febbraio 2024 Modifi...

Political stance in opposition to interventionist or expansionist policiesAnti-imperialist painting in Caracas, specifically targeting American imperialism. Written in Spanish Out with imperialism, only the people save the peopleAnti-imperialism in political science and international relations is opposition to imperialism or neocolonialism. Anti-imperialist sentiment typically manifests as a political principle in independence struggles against intervention or influence from a global superpow...

В Википедии есть статьи о других людях с фамилией Маршак. Роберт Юджин Маршакангл. Robert Eugene Marshak Дата рождения 11 октября 1916(1916-10-11)[1] Место рождения Бронкс Дата смерти 23 декабря 1992(1992-12-23)[1] (76 лет) Место смерти Канкун Страна США Род деятельности физик, ...

American punk band Naked RaygunNaked Raygun performing in Gainesville, Florida, 2007Background informationOriginChicago, IllinoisGenresPunk rock, post-hardcore, post-punkYears active1980–1992, 2006–presentLabelsRuthless Records, Homestead, Quarterstick Records, Caroline, Riot Fest Records, Wax Trax! RecordsMembersJeff PezzatiBill StephensEric SpicerFritz DorezaPast membersSantiago DurangoJohn HaggertyPierre KezdyBobby StrangeJim ColaoMarko PezzatiCamilo GonzalezJohn LundinSensitive PeteWe...

Blue BoxSampul tankōbon volume pertama, menampilkan Chinatsu Kano dan Taiki Inomataアオのハコ(Ao no Hako)GenreKomedi romantis[1]Olahraga[2][3] MangaPengarangKouji MiuraPenerbitShueishaPenerbit bahasa InggrisNA Viz MediaImprintJump ComicsMajalahWeekly Shōnen JumpDemografiShōnenTerbit12 April 2021 – sekarangVolume16 Portal anime dan manga Blue Box (Jepang: アオのハコcode: ja is deprecated , Hepburn: Ao no Hako) adalah sebuah seri manga komedi rom...



