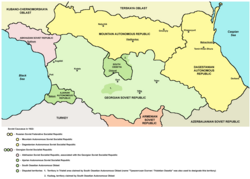
Аджарская Автономная Советская Социалистическая Республика

АССР
Аджарская Автономная Советская Социалистическая Республика
груз. აჭარის ავტონომიური საბჭოთა სოციალისტური რესპუბლიკა
41°39′ с. ш. 42°00′ в. д.HGЯO
Страна Флаг СССР СССР
Входила в Грузинская ССР
Адм. центр Батуми
История и география
Дата образования 1921—1990
Дата упразднения 1990
Площадь 3,0 тыс.
Население
Население 310 тыс. чел. (1969)
Национальности грузины
Официальный язык грузинский, русский
Орден Ленина — 1967 Орден Октябрьской Революции — 1971 Орден Дружбы народов  — 1972

Аджа́рская Автоно́мная Сове́тская Социалисти́ческая Респу́блика — административно-территориальная единица в составе Грузинской ССР, существовавшая в 1921—1990 годах. Столица — город Батуми.

Марка «50 лет Аджарской АССР». Почта СССР 1971 г.

Была образована как автономия грузин-мусульман 16 июня 1921 года и первоначально называлась Автономная Социалистическая Советская Республика Аджаристан. 5 декабря 1936 была переименована в Аджарскую Автономную Советскую Социалистическую Республику. В декабре 1990 года преобразована в Аджарскую Автономную республику.

В административном отношении в конце своего существования Аджарская АССР делилась на 5 районов: Кедский, Кобулетский, Хелвачаурский, Хулойский и Шуахевский.

Административное деление

Первоначально Аджарская АССР была разделена на 5 уездов, которые делились на теми (волости). В 1925 году Батумский уезд был переименован в Чорохский и АТД республики стало выглядеть так:

Уезд Центр Теми
Аджарис-Цкальский уезд Аджарис-Цкали[груз.] Аджарис-Агматский, Дологанский
Кедский уезд Кеди Кедский, Мериский, Цхмориский
Кобулетский уезд Кобулети Кинтришский, Кобулетский, Чаквский, Чахатский
Хулоский уезд Хуло Дорясомский, Карадерский, Рикетский, Схалтский, Учаштский, Хулоский, Чванский
Чорохский уезд Батум Гонеский, Кахаберский, Ортабатомский

В ходе административной реформы 1929—1930 годов уезды были преобразованы в районы, а их число уменьшилось сначала до 4 (Батумский, Кедский, Кобулетский и Хулойский)[1], а потом до 3 (упразднён Батумский район)[2], вскоре, однако, восстановленный. В 1934 году АТД Аджарии выглядело так[3]:

В 1952 году был образован пятый район — Шуахевский.

Руководство республики

Почтовая марка. 1960 год

Аджарский областной комитет КП(б) — КП Грузии

Основная статья: Аджарский областной комитет КП Грузии

ЦИК-Верховный Совет

ВРК-СНК-СМ

Военный гарнизон Аджарии

Почётное Революционное Знамя 1-я Кавказская горно-стрелковая дивизия им. ЦИК ССР Грузии. Музей дивизии, Майкоп 2013.

В январе 1921 года 9-я стрелковая дивизия переброшена в Закавказье для установления советской власти на Кавказе. 25 февраля дивизия в составе 11-й армии вошла в Тбилиси, а в середине марта в Батуми.

29.02.1928 года к 10 летию РККА дивизия награждается Почётным Революционным Красным Знаменем за выдающиеся заслуги перед Родиной и высокие показатели в боевой учёбе. Правительство Грузии, учитывая особые заслуги в деле укрепления советской власти в Закавказье взяло шефство над дивизией. Ей присваивается наименование «имени ЦИК ССР Грузии».

Отныне дивизия именуется 1-я Кавказская Краснознамённая стрелковая дивизия имени ЦИК ССР Грузии. В 1931 году дивизия переформировывается в горнострелковую дивизию.[4] 22 марта 1936 года дивизия награждаетсяОрденом Красной Звезды.

21.05.1936 года переименована и носила название 9-я горнострелковая Краснознамённая ордена Красной Звезды дивизия имени ЦИК ССР Грузии. В декабре 1942 года 9-я горнострелковая дивизия (СССР) перебрасывается под Туапсе для участия в Краснодарской наступательной операции.

Боевые Знамёна

  • Боевое Знамя.1-я Стрелковая Кавказская дивизия. Музей 9-й мсд. Майкоп.
    Боевое Знамя.1-я Стрелковая Кавказская дивизия. Музей 9-й мсд. Майкоп.
  • Боевое Знамя.1-я Стрелковая Кавказская дивизия (реверс).
    Боевое Знамя.1-я Стрелковая Кавказская дивизия (реверс).
  • Боевое Знамя 1-й Кавказской гсд. Музей 9-й мсд. Майкоп.
    Боевое Знамя 1-й Кавказской гсд. Музей 9-й мсд. Майкоп.
  • Боевое Знамя 1-й Кавказской гсд (реверс).
    Боевое Знамя 1-й Кавказской гсд (реверс).
  • Боевое Знамя.306-й стр. полк-ныне 1-й стр. Кавказский полк им. ЦИК Аджарской АССР. Музей 9-й мсд. Майкоп.
    Боевое Знамя.306-й стр. полк-ныне 1-й стр. Кавказский полк им. ЦИК Аджарской АССР. Музей 9-й мсд. Майкоп.
  • Боевое Знамя. 306-й стр. полк-ныне 1-й стр. Кавказский полк им. ЦИК Аджарской АССР (реверс).
    Боевое Знамя. 306-й стр. полк-ныне 1-й стр. Кавказский полк им. ЦИК Аджарской АССР (реверс).
  • Боевое Знамя. 4-й Стрелковый Грузинский полк 1-й Кавказской сд (гсд). Музей 9-й мсд. Майкоп.
    Боевое Знамя. 4-й Стрелковый Грузинский полк 1-й Кавказской сд (гсд). Музей 9-й мсд. Майкоп.
  • Боевое Знамя. 4-й Стрелковый Грузинский полк 1-й Кавказской сд (гсд) (реверс).
    Боевое Знамя. 4-й Стрелковый Грузинский полк 1-й Кавказской сд (гсд) (реверс).
  • Боевое Знамя. 7-й ГРУЗИНСКИЙ ГОРНЫЙ СТРЕЛКОВЫЙ ПОЛК 1-й Кавказской гсд. Музей 9-й мсд. Майкоп 2014.
    Боевое Знамя. 7-й ГРУЗИНСКИЙ ГОРНЫЙ СТРЕЛКОВЫЙ ПОЛК 1-й Кавказской гсд. Музей 9-й мсд. Майкоп 2014.
  • Боевое Знамя (реверс)7-й ГРУЗИНСКИЙ ГОРНЫЙ СТРЕЛКОВЫЙ ПОЛК (реверс) 1-й Кавказской гсд.
    Боевое Знамя (реверс)7-й ГРУЗИНСКИЙ ГОРНЫЙ СТРЕЛКОВЫЙ ПОЛК (реверс) 1-й Кавказской гсд.

Примечания

  1. ↑ Административно-территориальное деление Союза ССР по данным на 15 ноября 1930 г. — М., 1930. Дата обращения: 27 апреля 2019. Архивировано 18 июля 2020 года.
  2. ↑ Административно-территориальное деление Союза ССР. — М., 1931. Дата обращения: 27 апреля 2019. Архивировано 18 июля 2020 года.
  3. ↑ Административно-территориальное деление Союза ССР на 15 июля 1934 года. — М., 1934. Дата обращения: 27 апреля 2019. Архивировано 18 апреля 2019 года.
  4. ↑ Приказ Командующего Кавказской Краснознамённой Армии № 261/39 1931 г.

Read other articles:

Penghilangan rambut

Untuk kehilangan rambut, lihat Alopecia. Artikel ini perlu dikembangkan dari artikel terkait di Wikipedia bahasa Inggris. (November 2023) klik [tampil] untuk melihat petunjuk sebelum menerjemahkan. Lihat versi terjemahan mesin dari artikel bahasa Inggris. Terjemahan mesin Google adalah titik awal yang berguna untuk terjemahan, tapi penerjemah harus merevisi kesalahan yang diperlukan dan meyakinkan bahwa hasil terjemahan tersebut akurat, bukan hanya salin-tempel teks hasil terjemahan mesi...

 

Giovanni Battista Pergolesi

Giovanni Battista Pergolesi Giovanni Battista Pergolesi (4 Januari 1710 – 16 Maret 1736) adalah seorang komposer barok Italia, pemain biola, dan organis. Karya-karyanya yang paling terkenal termasuk Stabat Mater dan opera La serva padrona (Pembantu Menjadi Nyonya). Komposisinya termasuk opera dan musik sakral. Dia meninggal karena tuberkulosis pada usia 26 tahun. Pergolesi adalah salah satu komposer awal yang paling penting dari opera buffa (opera komik). Serial operanya, Il p...

 

Pembekuan hujan

Bagian dari seri alamCuaca Musim kalender Dingin Semi Panas Gugur Musim tropis Kemarau Harmattan Hujan Badai Awan Awan kumulonimbus Awan arcus Angin kencang Microburst Heat burst Derecho Petir Badai petir Badai petir massa udara Salju petir Badai petir kering Mesosiklon Supercell Tornado Tornado antisiklon Landspout Sengkayan Puting beliung Pusaran api Antisiklon Siklon Tekanan rendah kutub Siklon ekstratropis Angin ribut Eropa Nor'easter Siklon subtropis Siklon tropis Hurikan Atlantik Topan ...

Kleopatra Selene II

Cleopatra Selene IIIbu suri NumidiaIbu suri MauretaniaPatung dada Romawi kuno Cleopatra Selene II, Ratu Mauretania, atau ibunya Cleopatra VII dari Mesir, Museum Arkeologi Cherchell, Aljazair[1]Kelahiran40 SM (diyakini, tanggal pasti tidak diketahui)Alexandria, MesirKematian6 SMCaesarea, Kerajaan MauretaniaPemakamanMausoleum Kerajaan MauretaniaNama lengkapCleopatra SeleneAyahMarkus AntoniusIbuCleopatra VII PhilopatorPasanganJuba II dari NumidiaAnakPtolemy, Raja MauretaniaDrusilla Cleop...

 

Battle of Itea

1827 naval battle in the Gulf of Corinth during the Greek War of Independence Battle of IteaPart of the Greek War of IndependencePainting depicting the Battle of Iteaby Yiannis PoulakasDate30 September 1827Locationoff Itea, Aegean SeaResult Greek victoryBelligerents First Hellenic Republic Ottoman Empire Eyalet of EgyptCommanders and leaders Frank Abney HastingsStrength 4 ships 3 schooners3 brigs3 transport ships1 gunboatCasualties and losses unknown 7 ships destroyedtwo captured vteGreek War...

 

Kim Källström

Kim Källström Källström pada tahun 2015Informasi pribadiNama lengkap Kim Mikael Källström[1]Tanggal lahir 24 Agustus 1982 (umur 41)Tempat lahir Sandviken, SwediaTinggi 1,83 m (6 ft 0 in)[2]Posisi bermain GelandangKarier junior1986–1989 Sandvikens1990–1996 Partille1997–1998 HäckenKarier senior*Tahun Tim Tampil (Gol)1999–2001 Häcken 69 (14)2001–2003 Djurgårdens 48 (26)2004–2006 Rennes 83 (20)2006–2012 Lyon 204 (17)2012–2015 Spartak M...

Gereja Katolik di Yunani

Gereja Katolik di YunaniYunani: Καθολική Εκκλησία στην ΕλλάδαKatedral Basilika Santo Dionisius orang Areopagus, AthenaJenisKebijakan nasionalPenggolonganGereja Katolik RomaBadanpemerintahanKonferensi Waligereja YunaniPausPaus FransiskusNunsius ApostolikSavio HonWilayah YunaniBahasaYunani LatinPendiriPara rasul Santo Andreas Rasul dan Santo Rasul PaulusDidirikanAbad ke-1 Masehi Bagian dari seriGereja Katolik menurut negara Afrika Afrika Selatan Afrika Tengah ...

 

Potsie Weber

Fictional character from Happy Days Potsie redirects here. For other uses, see Potsy. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Potsie Weber – news · newspapers · books · scholar · JSTOR (April 2018) (Learn how and when to remove this message)Fictional character Potsie WeberPotsieFirst appearanceLove ...

 

Aoba-ku, Sendai

Aoba 青葉区Distrik kotaKantor Distrik AobaLokasi Distrik Aoba di wilayah SendaiNegaraJepangWilayahTōhokuPrefektur MiyagiKotaSendaiDidirikan1 April 1989Luas[1] • Total302,24 km2 (116,70 sq mi)Populasi (1 Desember 2023) • Total314,947 • Kepadatan1.042,04/km2 (2,698,9/sq mi)Zona waktuUTC+09:00 (JST)Kode pos980-8701Alamat kantor distrik1-5-1 Kamisugi, Aoba-ku, Sendai-shi, Miyagi-kenNomor telefon022-225-7211Situs webwww....

Islam in China

The percentage of Muslim population in the provinces of China, According to 2010 data. Part of a series onIslam in China History By dynasty Tang Song Yuan Ming Qing Rebellions and revolts Jahriyya revolt Panthay Rebellion (1856–1873) First Dungan Revolt (1862–1877) Second Dungan Revolt (1895–1896) Afaqi Khoja revolts Post-dynastic China 1912–present Second Sino-Japanese War Islamophobia Major figures Afaq Khoja Du Wenxiu Hu Dahai Hu Songshan Kasim Tuet Liu Zhi Ma Anliang Ma Bufang Ma...

 

Willard Saulsbury Jr.

American politician (1861–1927) Willard SaulsburyPresident pro tempore of the United States SenateIn officeDecember 14, 1916 – March 3, 1919Preceded byJames Paul ClarkeSucceeded byAlbert B. CumminsSecretary of the Senate Democratic CaucusIn officeMarch 4, 1913 – December 14, 1916LeaderJohn W. KernPreceded byWilliam E. ChiltonSucceeded byKey Pittman (Acting)United States Senatorfrom DelawareIn officeMarch 4, 1913 – March 3, 1919Preceded byHarry A. RichardsonS...

 

Maglev

Train system using magnetic levitation This article is about transportation. For the phenomenon, see Magnetic levitation. For other uses, see Maglev (disambiguation). The neutrality of this article is disputed. Relevant discussion may be found on the talk page. Please do not remove this message until conditions to do so are met. (May 2023) (Learn how and when to remove this message) Transrapid 09 at the Emsland test facility in Lower Saxony, Germany A full trip on the Shanghai Transrapid magl...

Battaglia di Lobositz

Battaglia di Lobositzparte della guerra dei sette anniSchema tattico della battaglia di LobositzData1º ottobre 1756 LuogoLovosice, Boemia (attuale Repubblica Ceca) EsitoVittoria prussiana Schieramenti Prussia Sacro Romano Impero ComandantiFederico il GrandeMaximilian Ulysses Browne Effettivi28.000 uomini33.354 uomini Perdite2.863 tra morti e feriti2.873 tra morti e feriti Voci di battaglie presenti su Wikipedia Manuale V · D · MGuerra dei sette anniBoemia e MoraviaPirna...

 

1992年大韓民國總統選舉

1992年大韓民國總統選舉 ← 1987 1992年12月18日 1997 → 投票率81.89% (▼7.26%)   获提名人 金泳三 金大中 鄭周永 政党 民主自由黨 民主黨 統一國民黨（朝鲜语：통일국민당 (대한민국)） 民選得票 9,977,332 8,041,284 3,880,067 得票率 41.96% 33.82% 16.31% 選舉得票圖   金泳三勝出選區  金大中勝出選區 选前總統 盧泰愚 无党籍 當選總統 金泳三 民主自由黨 1992年�...

 

Innsbruck Festival of Early Music

Ambras Castle, one of the festival's main concert venues The Innsbruck Festival of Early Music (German: Innsbrucker Festwochen der Alten Musik) is a festival of historically informed performances of music from the late Renaissance, Baroque and early Classical periods which takes place annually in Innsbruck, Austria. It was founded in 1976.[1] History The festival had its roots in 1963 when the Innsbruck musician Otto Ulf (1907–1993) organized a concert at the Ambras Castle to celebr...

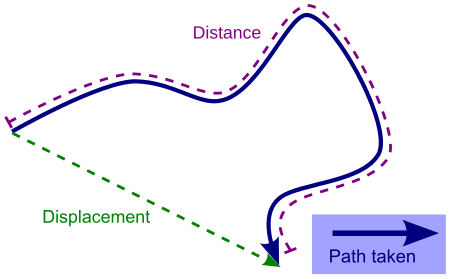
Displacement (geometry)

Vector relating the initial and the final positions of a moving point DisplacementDisplacement versus distance travelled along a pathCommon symbolsdSI unitmetreIn SI base unitsmDimensionL Part of a series onClassical mechanics F = d p d t {\displaystyle {\textbf {F}}={\frac {d\mathbf {p} }{dt}}} Second law of motion History Timeline Textbooks Branches Applied Celestial Continuum Dynamics Kinematics Kinetics Statics Statistical mechanics Fundamentals Acceleration Angular momentum Cou...

 

FESOM

Simulation of ocean circulation FESOM (Finite-Element/volumE Sea ice-Ocean Model)Developer(s)AWIInitial releaseJanuary 2004; 20 years ago (2004-01)Stable release1.4 / January 2014; 10 years ago (2014-01) Written inFortranTypeComputer simulationWebsitefesom.de FESOM (Finite-Element/volumE Sea ice-Ocean Model) is a multi-resolution ocean general circulation model that solves the equations of motion describing the ocean and sea ice using finite-eleme...

 

نزاع ألاسكا الحدودي

ادعاءات تملك ألاسكا المختلفة قبل التحكيم في 1903 نزاع ألاسكا الحدودي هو نزاع إقليمي بين الولايات المتحدة الأمريكية والمملكة المتحدة، حينما كانت الأخيرة تتحكم بالسياسة الخارجية لكندا وفقًا لقانون الاتحاد. حُل النزاع عبر التحكيم القضائي عام 1903. كان النزاع قائمًا منذ عام 1821 ب...

NGC 3704

NGC 3704   الكوكبة الباطية[1]  رمز الفهرس NGC 3704 (الفهرس العام الجديد)2MASX J11300472-1132462 (Two Micron All-Sky Survey, Extended source catalogue)PGC 35435 (فهرس المجرات الرئيسية)MCG-02-29-037 (فهرس المجرات الموروفولوجي)GSC 05512-00723 (دليل النجم المفهرس)6dFGS gJ113004.7-113246 (6dF Galaxy Survey)NPM1G -11.0300 (Lick Northern Proper Motion Survey Galaxy Calalogue)LEDA 3543...

 

Gruppo quoziente

In matematica, un gruppo quoziente è una particolare struttura algebrica che è possibile costruire a partire da un dato gruppo e un suo sottogruppo normale. Indice 1 Definizione 1.1 Premessa 1.2 Gruppo quoziente 2 Struttura di gruppo 3 Proiezione 4 Note 5 Bibliografia 6 Voci correlate Definizione Premessa Sia G {\displaystyle G} un gruppo, e H {\displaystyle H} un suo sottogruppo normale. Si può introdurre la relazione di equivalenza su G {\displaystyle G} definita, per ogni g , g ′...