Vârf (geometrie)
|
Read other articles:

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Huang Taiji Kaisar kedua Dinasti QingBerkuasa1626 – 21 September 1643PendahuluNurhaciPenerusKaisar ShunzhiInformasi pribadiKelahiran28 November ...

Scott Walker Scott Kevin Walker (lahir 2 November 1967) adalah seorang politikus asal Amerika Serikat yang menjabat sebagai Gubernur Wisconsin ke-45 dari 2011 sampai 2019. Ia adalah anggota Partai Republik. Bacaan tambahan Cramer, Katherine J. The politics of resentment: rural consciousness in Wisconsin and the rise of Scott Walker (University Of Chicago Press, 2016) Stein, Kate (July 19, 2015). Timeline: The Life and Career of Scott Walker. Wisconsin State Journal. Diakses tanggal November 2...

2008 2015 (élections départementales) Élections cantonales françaises de 2011 20 mars 2011(1er tour)27 mars 2011(2d tour) Type d’élection Cantonales Corps électoral et résultats Inscrits au 1er tour 21 295 938 Votants au 1er tour 9 439 097 44,32 % 20,6 Votes exprimés au 1er tour 9 160 604 Blancs et nuls au 1er tour 278 493 Inscrits au 2d tour 19 015 771 Votants au 2d tour 8 513 399 44,77 %...

This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. Please help improve it by rewriting it in an encyclopedic style. (November 2009) (Learn how and when to remove this template message) War and Peace in the Global Village AuthorsMarshall McLuhan, Quentin FioreCountryUnited StatesLanguageEnglishPublication date1968Media typePrint War and Peace in the Gl...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Koi to Yobu ni wa Kimochi Warui恋と呼ぶには気持ち悪いGenreKomedi romantis MangaPengarangMogusuPenerbitIchijinshaMajalahComic POOLDemografiJoseiTerbit25 Januari, 2015 – 25 Maret, 2021Volume8 Seri animeSutradaraNaomi NakayamaProduserShunsuke...

American aerospace engineer and ULA CEO Tory BrunoBruno in December 2019BornSalvatore Thomas Bruno (1961-11-03) November 3, 1961 (age 62)Monterey, California, U.S.NationalityAmericanAlma materCalifornia Polytechnic State University (BS)TitlePresident and Chief Executive Officer of United Launch Alliance Tory Bruno (born November 3, 1961, as Salvatore Thomas Bruno) is an American aerospace engineer and executive. He has been the CEO of United Launch Alliance (ULA) since August 2014. ...

Marco Friedl Friedl nel 2017 Nazionalità Austria Altezza 187 cm Peso 71 kg Calcio Ruolo Difensore Squadra Werder Brema Carriera Giovanili 2002-2007SV Kirchbichl2007-2008 Kufstein2008-2017 Bayern Monaco Squadre di club1 2015-2018 Bayern Monaco II14 (1)2017-2018 Bayern Monaco1 (0)2018-2019 Werder Brema II1 (0)2018- Werder Brema104 (5) Nazionale 2013 Austria U-152 (2)2013-2014 Austria U-168 (1)2014-2015 Austria U-173 (0)2015-2016 Austria U-182 (0)2016-...

AquamanPoster rilis teatrikal IndonesiaIndeks kartuSutradaraJames WanProtagonis Jason Momoa Amber Heard Willem Dafoe Patrick Wilson Dolph Lundgren Yahya Abdul-Mateen II Nicole Kidman Produksi seni pertunjukan Peter Safran Rob Cowan Naskah David Leslie Johnson-McGoldrick Will Beall MusikRupert Gregson-WilliamsFotografiDon Burgess Penyuntingan filmKirk M. Morri BusanaKym Barrett Rumah produksiWarner Bros. dan The Safran Company DistributorWarner Bros. PicturesPenampilan perdana 26 November 201...

Ini adalah nama Telugu; marganya adalah Petla. Puri Jagannadh(పూరి జగన్నాధ్)LahirPuri Jagannadh28 September 1966 (umur 57)Kothapalli[perlu disambiguasi], Andhra Pradesh, India[1]Tempat tinggalHyderabad, Telangana, IndiaNama lainJaganPekerjaanSutradara, Produser, Penulis naskah, Pemeran, Penulis ceritaTahun aktif2000–sekarangSuami/istriLavanyaAnak3KerabatSairam Shankar (saudara)Situs webpurijagan.com Puri Jagannadh[2] (lahir 28 S...

Civil event in Russia You can help expand this article with text translated from the corresponding article in Russian. (May 2022) Click [show] for important translation instructions. View a machine-translated version of the Russian article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text int...

1920 Men's Olympic Football TournamentTournament detailsHost countryBelgiumDates28 August – 5 September 1920Teams15 (from 2 confederations)Venue(s)4 (in 3 host cities)Final positionsChampions Belgium (1st title)Runners-up SpainThird place NetherlandsFourth place ItalyTournament statisticsMatches played17Goals scored70 (4.12 per match)Attendance150,600 (8,859 per match)Top scorer(s) Herbert Carlsson (7 goals)← 1912 1924 → Internationa...

لمعانٍ أخرى، طالع هيلزبورو (توضيح). هيلزبورو الإحداثيات 40°50′11″N 91°42′49″W / 40.836388888889°N 91.713611111111°W / 40.836388888889; -91.713611111111 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة هنري خصائص جغرافية المساحة 1.310903 كيلومتر مربع1....

Oil pipeline in North America Keystone Pipeline System(partly operational and proposed)Keystone Pipeline routeLocationCountryCanadaUnited StatesGeneral informationTypeCrude oilOwnerTC EnergyWebsitewww.tcenergy.com/operationsKeystone Pipeline(Phase 1)LocationFromHardisty, AlbertaPasses throughRegina, SaskatchewanSteele City, NebraskaToWood River, IllinoisPatoka, Illinois (end)General informationTypeCrude oilStatusCompleteConstruction startedQ2 2008CommissionedJune 2010[1]Technical info...

Scottish geographer, zoologist, and botanist (1762–1829) Francis Buchanan-HamiltonFRSE FRS FLSBornFrancis Buchanan(1762-02-15)15 February 1762Callander, PerthshireDied15 June 1829(1829-06-15) (aged 67)Other namesFrancis Hamilton, formerly Buchanan; Francis Hamilton; Buchanan-Hamilton; Francis Hamilton Buchanan; Francis Buchanan HamiltonEducationUniversity of EdinburghKnown forAn account of the fishes found in the river Ganges and its branchesAwardsFellow of the Royal Society ...

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المخصصة لذلك. (مايو 2020) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وص�...

القوات البحرية الاندونيسية شعار القوات البحرية الاندونيسية. الدولة إندونيسيا الإنشاء 1945-الآن النوع قوات بحرية الحجم 74 الف جزء من القوات المسلحة الإندونيسية شعار نصي نحن منتصر في البحر الاشتباكات غزو بحر آرو الموقع الرسمي http://www.tnial.mil.id/ القادة القائد الحالي أدميرال ما�...

1989 Indian general election ← 1984 22 and 26 November 1989[1] 1991 → ← outgoing memberselected members →529 of the 543 seats in the Lok Sabha265 seats needed for a majorityRegistered498,906,129Turnout61.95% ( 2.06pp) First party Second party Leader Rajiv Gandhi V. P. Singh Party INC(I) JD Alliance INC (I)+ JD+ Leader's seat Amethi Fatehpur Last election 46.86%, 414 seats 13.50%, 14 seats Seats won 197 143 Seat&...
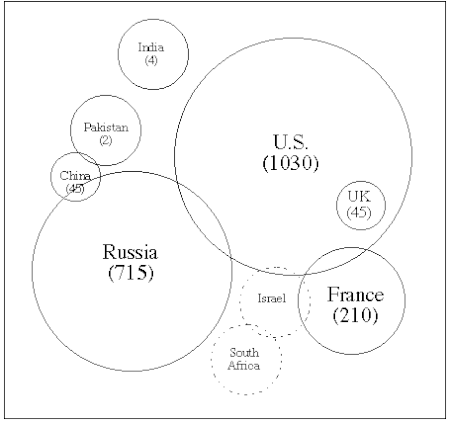
Spread of nuclear weapons See also: Chemical weapon proliferation For the card game, see Nuclear Proliferation (card game). Nuclear weapons Background Nuclear explosion History Warfare Design Testing Delivery Yield Effects Workers Ethics Arsenals Target selection Arms race Blackmail Espionage Proliferation Disarmament Terrorism Opposition Winter Nuclear-armed states NPT recognizedUnited States Russia United Kingdom France China OthersIndia Israel (undeclared) Pakistan North Korea FormerS...

Tómas Ingi TómassonNazionalità Islanda Calcio RuoloAllenatore (ex attaccante) Termine carriera2003 CarrieraSquadre di club1 1986-1990 ÍBV Vestmannæyja66 (34)1990-1991→ FC Berlino4 (3)1991-1992 ÍBV Vestmannæyja25 (9)1993-1994 KR Reykjavík34 (14)1995 Grindavík15 (7)1996-1997 Raufoss27 (11)1998 Þróttur18 (14)1999-2000 Aarhus37 (5)2000 ÍBV Vestmannæyja6 (1)2000 Aarhus3 (2)2001-2002 ÍBV Vestmannæyja29 (12)2003 KFS4 ...

Overview of the Islamic perspectives on the death of Jesus This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: major overcite at present in some sections, particularly in the lead; more inline citations are needed in others. Please help improve this article if you can. (August 2022) (Learn how and when to remove this message) Part of a series on Jesus in Christianity Christ Christology Names and titles Life of Jesus Gospels Gospel harmony Places Vi...






