Spațiu simplu conex
|
Read other articles:

artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Untuk orang lain dengan nama yang sama, lihat John Chiang. Ini adalah nama Tionghoa; marganya adalah Chiang (江). Johnny ChiangChiang Chi-chen江...

Совреме́нные ми́фы — культурные явления, обладающие мифологической природой, но зародившиеся и существующие в культуре научно-рационального общества[1]. Явление современного мифа соотносится с процессами ремифологизации как стратегией толкования мифа, как зна�...

Shoot to ThrillLagu oleh AC/DCdari album Back in BlackDirilis25 July 1980Direkam1980GenreHard rockDurasi5:17LabelAtlanticPencipta Angus Young Malcolm Young Brian Johnson ProduserRobert John Mutt Lange Shoot to Thrill merupakan salah satu lagu dari band Rock and Roll asal Australia, AC/DC. Lagu ini merupakan lagu kedua dalam album Back in Black yang dirilis pada 25 Juni 1980.[1] Lagu ini juga merupakan lagu kedua dalam album AC/DC Live[2] dan AC/DC Live (1992, Special Collector...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (أبريل 2020) هذه قائمة رؤساء تونس حسب العمر. الجدول الأول يرسم عمر كل رئيس تونسي في وقت تنصيبه الرئيس (التنصيب الأول إذا...

France 3OccitanieCaractéristiquesCréation 1er janvier 2017Propriétaire France TélévisionsSlogan Vous êtes au bon endroitFormat d'image 1080i (HDTV)Langue FrançaisPays FranceSiège social ToulouseChaîne sœur France 3Site web France 3 OccitanieDiffusionAire Occitanie FranceDiffusion TNT française, satellite, câble, ADSL et webmodifier - modifier le code - modifier Wikidata Le 24 septembre 1974, vue des manifestants devant les bureaux de la ORTF. Aujourd'hui siege de France 3 Occitani...

2006 Newark mayoral election ← 2002 May 9, 2006 2010 → Candidate Cory Booker Ronald Rice Party Nonpartisan Nonpartisan Popular vote 32,134 10,337 Percentage 72.15% 23.21% Mayor before election Sharpe James Democratic Elected Mayor Cory Booker Democratic Elections in New Jersey Federal government U.S. President 1788-89 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844 1848 1852 1856 1860 1864 1868 1872 1876 1880 1884 1888 1892 1896 1900 19...

Metropolitan region in the Kansai region of Japan Major metropolitan area of JapanKeihanshin Kyoto–Osaka–Kobe Kinki MMAMajor metropolitan area of JapanOsakaKyotoKobeKeihanshin Major Metropolitan AreaCoordinates: 34°50′N 135°30′E / 34.833°N 135.500°E / 34.833; 135.500CountryJapanPrefecturesKyotoOsakaHyōgoArea • Metro13,228 km2 (5,107 sq mi)Population (October 1, 2015)[1] • Metro19,302,746 • Met...

Inventor of basketball (1861–1939) For the chemical biologist, see James Naismith (chemist). James NaismithNaismith holding a basketball and basketBiographical detailsBorn(1861-11-06)November 6, 1861Almonte, Canada West, Province of CanadaDiedNovember 28, 1939(1939-11-28) (aged 78)Lawrence, Kansas, U.S.Alma materMcGill UniversitySpringfield CollegePresbyterian CollegeCoaching career (HC unless noted)Basketball1898–1907KansasTrack and field1900–1906Kansas Head coaching recordOv...

Ignaz Philipp SemmelweisIgnace Philippe Semmelweis (1860)BiographieNaissance 1er juillet 1818Tabán (royaume de Hongrie, empire d'Autriche)Décès 13 août 1865 (à 47 ans)Oberdöbling (en) (empire d'Autriche)Sépulture Musée Semmelweis sur l'histoire de la médecineNationalités autrichiennehongroiseFormation Gymnase catholique de Budapest (d) (jusqu'en 1835)Université Loránd-Eötvös (jusqu'en 1841)Université de Vienne (jusqu'en 1844)Activités Médecin, gynécologue, obstétricien...

SibolangitKecamatanGreen Hill SibolangitSibolangitPeta lokasi Kecamatan SibolangitKoordinat: 3°16′47″N 98°33′10″E / 3.279636°N 98.552650°E / 3.279636; 98.552650Koordinat: 3°16′47″N 98°33′10″E / 3.279636°N 98.552650°E / 3.279636; 98.552650Negara IndonesiaProvinsiSumatera UtaraKabupatenDeli SerdangPemerintahan • CamatFebri Gurusinga, S.STP, MSP[1]Populasi (2021)[2] • Total20...

English comedy actor (1920–1988) For other people also known as Jimmy Edwards or James Edwards, see James Edwards (disambiguation). Jimmy EdwardsDFCEdwards at a book launch, 1966BornJames Keith O'Neill Edwards(1920-03-23)23 March 1920Barnes, Surrey, EnglandDied7 July 1988(1988-07-07) (aged 68)London, EnglandResting placeThe Parish Church of St. Andrew and St. Mary the Virgin, Fletching, East Sussex, EnglandOccupationComedy actorYears active1946–1988Spouse Valerie Seymour ...

John La Gatta (1924) John La Gatta (May 26, 1894 – January 21, 1977), also spelled LaGatta, was an advertising illustrator active during the first half of the 20th century. Early life John La Gatta was born in Naples, Italy, the son of an educated father and a mother from an old and well-connected family which traced their origins back to the Count of Anjou, brother of King Louis IX of France.[1] La Gatta was a sickly child. Around the age of four his mother died in childbirth. The ...

Федеральное агентство по делам Содружества Независимых Государств, соотечественников, проживающих за рубежом, и по международному гуманитарному сотрудничествусокращённо: Россотрудничество Общая информация Страна Россия Юрисдикция Россия Дата создания 6 сентября...

Voce principale: Associazione Calcio Reggiana 1919. AC ReggianaStagione 1993-1994 Sport calcio Squadra Reggiana Allenatore Giuseppe Marchioro Presidente Gianfranco Morini Serie A14º Coppa ItaliaSecondo turno Maggiori presenzeCampionato: Sgarbossa (34)Totale: Sgarbossa (35) Miglior marcatoreCampionato: Padovano (10)Totale: Padovano (10) StadioMirabello Abbonati10 252 Maggior numero di spettatori15 379 vs Juventus(6 febbraio 1994) Minor numero di spettatori11 677 vs Lecce(...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

Sections of the Great Wall of China built during the Ming dynasty (1368-1644) The Great Wall at Mutianyu. This and many other famous sections of the Great Wall were built during the Ming dynasty. The extent of the Ming dynasty and its walls, which formed most of what is called the Great Wall of China today The Ming Great Wall (Chinese: 明長城; pinyin: Ming changcheng), built by the Ming dynasty (1368–1644), forms the most visible parts of the Great Wall of China today. A comprehe...
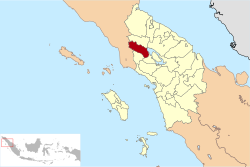
Peta Lokasi Kabupaten Dairi di Sumatera Utara Berikut adalah daftar kecamatan dan kelurahan/desa di Kabupaten Dairi, Sumatera Utara, Indonesia.Kabupaten Dairi terdiri dari 15 kecamatan, 8 kelurahan, dan 161 desa dengan luas wilayah mencapai 1.927,80 km² dan jumlah penduduk sekitar 322.748 jiwa (2017) dengan kepadatan penduduk 167 jiwa/km².[1][2] Daftar kecamatan dan kelurahan di Kabupaten Dairi, adalah sebagai berikut: Kode Kemendagri Kecamatan Jumlah Kelurahan Jumlah Desa S...

رادي أفراموفيتش معلومات شخصية الميلاد 29 نوفمبر 1949 (العمر 74 سنة) الطول 194 سنتيمتر مركز اللعب حارس مرمى الجنسية صربيا المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1969–1974 بوراتس تشاتشاك [الإنجليزية] - 1974–1979 رييكا 119 (0) 1979–1983 نوتس كاونتي 149 (0) 1983 FC Inter-Montréal [الإنجليزية]̴...

Asia Tengah Peta Asia Tengah menampilkan tiga perbatasan Eurasia untuk kawasan tersebut Asia Tengah Soviet merujuk kepada belahan Asia Tengah yang dulunya dikuasai oleh Uni Soviet, serta melewati masa pemerintahan Uni Soviet (1918–1991). RSS Asia Tengah menyatakan kemerdekaan pada 1991. Dalam hal wilayah, wilayah tersebut nyaris merupakan sinonim dengan Turkestan Rusia, nama untuk kawasan tersebut pada masa Kekaisaran Rusia. Asia Tengah Soviet melewati banyak pembagian wilayah sebelum perba...

American journalist Carla RobbinsRobbins at the Halifax International Security Forum 2012BornCarla Anne Robbins1953NationalityAmericanEducationWellesley College (BA, 1974)University of California, Berkeley (MA, PhD)OccupationJournalistEmployer(s)BusinessWeek (1982–1986)U.S. News & World Report (1986–1992)The Wall Street Journal (1993–2006)The New York Times (2006–2012)AwardsPulitzer Prize for International Reporting (1999, shared)Pulitzer Prize for National Reporting (2000, shared...

![{\displaystyle F:[0,1]\times [0,1]\rightarrow X}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aef465a01c33e4ce60ee1507bbf350ba66ee7aca)






