Prim trunchiabil
|
Read other articles:

Artikel ini perlu diterjemahkan dari bahasa Inggris ke bahasa Indonesia. Artikel ini ditulis atau diterjemahkan secara buruk dari Wikipedia bahasa Inggris. Jika halaman ini ditujukan untuk komunitas bahasa Inggris, halaman itu harus dikontribusikan ke Wikipedia bahasa Inggris. Lihat daftar bahasa Wikipedia. Artikel yang tidak diterjemahkan dapat dihapus secara cepat sesuai kriteria A2. Jika Anda ingin memeriksa artikel ini, Anda boleh menggunakan mesin penerjemah. Namun ingat, mohon tidak men...

Bagian dari seri artikel mengenaiEnergi berkelanjutan Ikhtisar Energi berkelanjutan Bahan bakar karbon netral Penghapusan bertahap bahan bakar fosil Penghematan energi Kogenerasi Efisiensi energi Penyimpanan energi Bangunan hijau Pompa panas Tenaga rendah karbon Mikrogenerasi Desain bangunan surya pasif Energi terbarukan Bahan bakar hayati Panas bumi Pembangkit listrik tenaga air Surya Pasang surut Ombak Angin Transportasi berkelanjutan Kendaraan listrik Kendaraan hijau Hibrida plug-in ...

Payment order for a prepaid amount of money Postal money order, Duchy of Brunswick, 1867 A specimen money order of Italy c. 1879 A money order is a directive to pay a pre-specified amount of money from prepaid funds, making it a more trusted method of payment than a cheque. History The money order system was established by a private firm in Great Britain in 1762 and was expensive and not very successful. Around 1836 it was sold to another private firm which lowered the fees, significantly inc...

Public (gifted) school in Tehran, IranAlborz Mandegar High Schoolدبیرستان ماندگار البرزAddressCollege Crossroad, Enqelab StreetTehranIranInformationOther namesAmerican College of Tehran, Alborz CollegeSchool typePublic (Gifted)Founded1873; 151 years ago (1873)FounderJames BassettPrincipalMohammad MohammadiGrades10–12Enrollment1,850AlumniAlborziWebsiteMandegarAlborz.sch.ir Alborz High School (Persian: دبیرستان ماندگار البرز) is a coll...

Tifanny RaytamaLahirTifanny Citra Raytama22 Maret 1988 (umur 36) Jakarta, IndonesiaKebangsaan IndonesiaNama lainFanny Raytama, Tifanny CitraAlmamaterUniversitas Atma Jaya JakartaPekerjaan Aktris Presenter Tahun aktif2007 - sekarangSuami/istrirahasiaAnakKamini Mahlagha Raysala Tifanny Raytama atau Tifanny Citra Raytama (lahir 22 Maret 1988)[1] adalah pembawa acara berita Indonesia. Ia menjadi anchor dalam program berita Reportase dan pernah menjadi pembawa acara Jelajah...

Nggak Lagi LagiAlbum studio karya Itje TrisnawatiDirilis1983GenrePopLabelInsan RecordsKronologi Itje Trisnawati Karena Senyuman (1983)Karena Senyuman1983 Nggak Lagi Lagi (1983) Romeo Bercinta (1984)Romeo Bercinta1984 Romeo Bercinta merupakan album musik utama karya Itje Trisnawati. Dirilis pada tahun 1983. Lagu utamanya di album ini ialah Nggak Lagi Lagi. Daftar lagu Nggak Lagi Lagi Taburan Bunga Tak Seindah Khayalan Panah Merah Biarkan Aku Sendiri Tunas Cinta Yang Pertama Terlambat Pahla...

Cette page concerne l'année 917 du calendrier julien. Chronologies Données clés 914 915 916 917 918 919 920Décennies :880 890 900 910 920 930 940Siècles :VIIIe IXe Xe XIe XIIeMillénaires :-IIe -Ier Ier IIe IIIe Calendriers Romain Chinois Grégorien Julien Hébraïque Hindou Hégirien Persan Républicain modifier L'année 917 est une année commune qui commence un mercredi. Événements Afrique Au Maroc, l'émir de Nekor est...

Questa voce o sezione deve essere rivista e aggiornata appena possibile. Sembra infatti che questa voce contenga informazioni superate e/o obsolete. Se puoi, contribuisci ad aggiornarla. Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Atletico Roma Football Club. A.S. Cisco Calcio RomaStagione 2006-2007Sport calcio...

Questa voce sugli argomenti allenatori di calcio brasiliani e calciatori brasiliani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. Roque Júnior Nazionalità Brasile Altezza 186 cm Peso 83 kg Calcio Ruolo Allenatore (ex difensore) Termine carriera 2010 - giocatore Carriera Squadre di club1 1994-1995 São José47 (1)1995-2000 Palmeiras198 (17)2000-2003 Milan44 (0)2003-2004→ ...

Questa voce sugli argomenti imprenditori tedeschi e produttori cinematografici è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Foto della Library of Congress Paul Davidson (30 marzo 1867 – 18 luglio 1927) è stato un produttore cinematografico e imprenditore tedesco. Indice 1 Biografia 2 Filmografia 2.1 Produttore 3 Note 4 Altri progetti 5 Collegamenti esterni Biografia Prima di arrivare al cinema, Davidson lavorò nel settore dell'abbigliamento. Ne...

内華達州 美國联邦州State of Nevada 州旗州徽綽號:產銀之州、起戰之州地图中高亮部分为内華達州坐标:35°N-42°N, 114°W-120°W国家 美國建州前內華達领地加入聯邦1864年10月31日(第36个加入联邦)首府卡森城最大城市拉斯维加斯政府 • 州长(英语:List of Governors of {{{Name}}}]]) • 副州长(英语:List of lieutenant governors of {{{Name}}}]])喬·隆巴爾多(R斯塔...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要擴充。 (2013年1月1日)请協助改善这篇條目,更進一步的信息可能會在討論頁或扩充请求中找到。请在擴充條目後將此模板移除。 此條目需要补充更多来源。 (2013年1月1日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的...

India Malaysia மலேசிய இந்தியர்கள் Orang India MalaysiaParameswara பரமேசுவராSamy Vellu சாமிவேலு சங்கிலிமுத்துAnwar Ibrahimஅன்வர் இப்ராகீம்Deborah Priya Henry டெபோரா பிரியாGuy Sebastian கை செபாஸ்டியன்Nicol Davidநிகோல் டேவிட்Shuba Jay சுபாசிணி ஜெயரத்தினம்Karpal Si...

Football team in Birmingham, Alabama This article is about the team in the second edition of the USFL. For the team in the original USFL from the 1980s, see Birmingham Stallions. Birmingham Stallions Current seasonEstablished November 22, 2021; 2 years ago (2021-11-22)Play in Protective Stadium (Birmingham, Alabama) League/conference affiliationsUnited States Football League (2022–2023) South Division (2022–2023) United Football League (2024–present) USFL Conference (2...

Market town in Derbyshire, England This article is about the town in Derbyshire, England. For other uses, see Bakewell (disambiguation). Human settlement in EnglandBakewellBakewell town centreBakewell parish highlighted within DerbyshirePopulation3,949 [1]OS grid referenceSK2168Civil parishBakewellDistrictDerbyshire DalesShire countyDerbyshireRegionEast MidlandsCountryEnglandSovereign stateUnited KingdomPost townBAKEWELLPostcode districtDE45Dialling ...
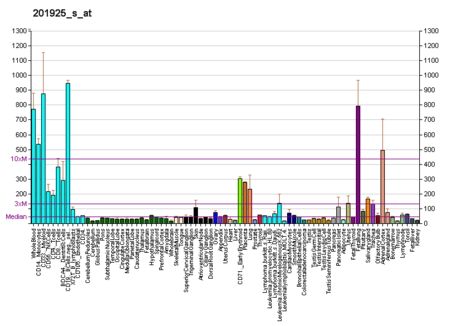
CD55 molecule (Cromer blood group) معرفات أسماء بديلة CR, CROM, complement decay-accelerating factor, CD55 molecule, decay accelerating factor for complement (Cromer blood group), CD55 antigen, DAF, CD55, TC, Cromer blood group antigen معرفات خارجية نمط التعبير عن الحمض النووي الريبوزي المزيد من بيانات التعبير المرجعية تماثلات متسلسلة أنواع الإنسان الفأر أنتريه n/a Ens...

الهيئة المصرية العامة للكتاب الهيئة المصرية العامة للكتابالشعار البلد مصر المقر الرئيسي القاهرة تاريخ التأسيس 1971 (منذ 53 سنة) المالك وزارة الثقافة النوع هيئة حكومية منطقة الخدمة مصر اللغات الرسمية العربية الرئيس أحمد بهي الدين[1] الموقع الرسمي gebo.gov.eg تعديل مصدري - ت...

281 BC–62 AD kingdom in northern Anatolia For other uses, see Pontus. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Kingdom of Pontus – news · newspapers · books · scholar · JSTOR (November 2019) (Learn how and when to remove this message) Kingdom of Pontus281 BC–62 ADThe Kingdom of Pontus at its heigh...
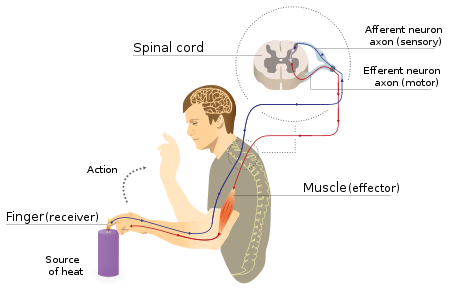
Neural pathway which controls a reflex In a reflex arc, an action potential can bypass the brain for processing and uses dedicated neural pathways for faster processing. When a stimulus (A) is encountered, the signal from that stimulus will travel up the sensory neuron (B, in green) to the spinal column (C). There it will likely pass through a short interneuron (D, in purple) before continuing down a motor neuron (E, in blue) to the origin of the signal. Then, a contraction of the muscles (F,...

South Korean footballer Lee Yong-rae Personal informationDate of birth (1986-04-17) 17 April 1986 (age 38)Place of birth Daejeon, South KoreaHeight 1.75 m (5 ft 9 in)Position(s) Defensive midfielderTeam informationCurrent team Daegu FCNumber 74Youth career2002–2004 Yuseong BST High School2002–2003 → FC Metz (KFA Youth Project)2005–2008 Korea UniversitySenior career*Years Team Apps (Gls)2009–2010 Gyeongnam FC 53 (10)2011–2017 Suwon Samsung Bluewings 71 (3)2014�...