Forța centrifugă
|
Read other articles:

Artur Nikolayevich ChilingarovArtur Nikolayevich Chilingarov mengunjungi Arkangelsk (22 Agustus 2009)Lahir25 September 1939 (umur 84)Leningrad, SFSR Rusia, Uni Soviet (sekarang St. Petersburg, Rusia)KebangsaanRusiaTahun aktif1963–sekarangDikenal atasPenjelajahan kutubPenghargaanPahlawan Uni SovietPahlawan RusiaOrdo LeninTanda tangan Artur Nikolayevich Chilingarov (Rusia: Артур Николаевич Чилингаровcode: ru is deprecated ; lahir 25 September 1939) adalah s...

Ini adalah nama Karo, marganya adalah Sitepu. Mehulika SitepuBerkas:Mehulika Sitepu.jpgLahir16 Juni 1980 (umur 43) Jakarta, IndonesiaPekerjaanPembawa acaraDikenal atasPresenter berita TV Mehulika Sitepu (lahir 16 Juni 1980) adalah pembawa acara berita Indonesia. Ia menjadi pembawa acara dalam program berita Lensa Indonesia Pagi dan Lensa Indonesia Sore di RTV. Karier Sejak 3 Mei 2014, dia bersama Prabu Revolusi dan Reinhard Sirait menjadi penyiar berita utama dalam acara Lensa Indonesia ...

This is a list of launches made by the R-7 Semyorka ICBM, and its derivatives between 2000 and 2004. All launches are orbital satellite launches, unless stated otherwise. Contents 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2...

Stasiun Hayato隼人駅Stasiun Hayato pada Mei 2018LokasiHayato-Chō Mitsugi, Kirishima(鹿児島県霧島市隼人町見次)Prefektur KagoshimaJepangKoordinat31°44′38″N 130°44′23″E / 31.7438°N 130.7397°E / 31.7438; 130.7397Koordinat: 31°44′38″N 130°44′23″E / 31.7438°N 130.7397°E / 31.7438; 130.7397Operator JR KyushuJalur ■ Jalur Utama Nippō ■ Jalur Hisatsu Letak434.7 km dari KokuraJumlah peron1 peron samping + 1...

Brad Friedel Informasi pribadiNama lengkap Bradley Howard FriedelTanggal lahir 18 Mei 1971 (umur 52)Tempat lahir Lakewood, Ohio, United StatesTinggi 6 ft 3 in (1,91 m)Posisi bermain Penjaga gawangKarier junior1990–1992 UCLAKarier senior*Tahun Tim Tampil (Gol)1994–1995 USSF 0 (0)1994 → Newcastle United (loan) 0 (0)1995 → Brøndby (pinjaman) 0 (0)1995–1996 Galatasaray 30 (0)1996–1997 Columbus Crew 38 (0)1997–2000 Liverpool 25 (0)2000–2008 Blackburn Rovers 28...

Ini adalah nama Batak Toba, marganya adalah Situngkir. Wilda SitungkirLahirWilda Octaviana Situngkir27 Oktober 1995 (umur 28)Pontianak, Kalimantan Barat, IndonesiaAlmamaterUniversitas Panca BhaktiPekerjaanModelratu kecantikanaktrisTinggi173 cm (5 ft 8 in)[1]Pemenang kontes kecantikanGelar Puteri Indonesia Kalimantan Barat 2018 Puteri Indonesia Pariwisata 2018(Miss Supranational Indonesia 2018) Warna rambutHitamWarna mataHitamKompetisiutama Miss Earth Indonesia 2017...

1953 aviation accident Transocean Air Lines Flight 512A Douglas DC-6A similar to the crash aircraftAccidentDateJuly 12, 1953SummaryUndetermined (aircraft never recovered)SiteApprox. 630 km (340 nmi) east of Wake Island, Pacific OceanAircraftAircraft typeDouglas DC-6AOperatorTransocean AirlinesRegistrationN90806Flight originGuam, US Territory1st stopoverWake Island, US Territory2nd stopoverHonolulu, Hawaii, US (Territory in 1953)DestinationOakland, California, USPassengers50Crew8Fatalitie...

Questa voce sugli argomenti allenatori di calcio ungheresi e calciatori ungheresi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti dei progetti di riferimento 1, 2. Márton Bukovi Bukovi nel 1976, durante un'intervista per la radio Nazionalità Ungheria Calcio Ruolo Attaccante Termine carriera 1935 - giocatore1967 - allenatore Carriera Squadre di club1 1920-1925 Ékszerészek? (?)1925-1926 Alba Roma16 (23)1926-1933&...
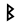
此條目介紹的是拉丁字母中的第2个字母。关于其他用法,请见「B (消歧义)」。 提示:此条目页的主题不是希腊字母Β、西里尔字母В、Б、Ъ、Ь或德语字母ẞ、ß。 BB b(见下)用法書寫系統拉丁字母英文字母ISO基本拉丁字母(英语:ISO basic Latin alphabet)类型全音素文字相关所属語言拉丁语读音方法 [b][p][ɓ](适应变体)Unicode编码U+0042, U+0062字母顺位2数值 2歷史發...

Aleksandr Yeliseyev With Krylia Sovetov in 2012Informasi pribadiNama lengkap Aleksandr Vladimirovich YeliseyevTanggal lahir 15 November 1991 (umur 32)Tinggi 1,83 m (6 ft 0 in)Posisi bermain GelandangInformasi klubKlub saat ini Krylia Sovetov SamaraNomor 32Karier senior*Tahun Tim Tampil (Gol)2009 FC Moscow (reserves) 2010– Krylia Sovetov Samara 14 (1)2011–2012 → Shinnik (loan) 21 (2) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik dan akura...

Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (March 2022) (Learn how and when to remove this message) Timeline of the war in Donbas201420152016201720182019202020212022 This is a timeline of the war in Donbas for the year 2021. January–March 1 January: The Ukrainian press centre of the Ukrainian Joint Forces reported nine pro-Russian violations of ...

Modul Lexus IS 250 dengan tombol asisten darurat (SOS) Safety Connect Safety Connect adalah sistem telematika berbasis subskripsi yang diperkenalkan oleh Toyota Motor Corporation tahun 2009 untuk merek Toyota dan Lexus. Sistem ini menyediakan fasilitas komunikasi, roadside assistance, keamanan kendaraan, diagnostik jarak jauh, dan berbagai layanan lainnya. Tidak seperti Lexus Link yang ada pada model-model Lexus sebelumnya, sistem Safety Connect bersifat eksklusif dan tidak perlu lisensi dari...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Public beach in Revere, Massachusetts, U.S. Revere Beach ReservationRevere Beach in 2004Location in MassachusettsShow map of MassachusettsRevere Beach (the United States)Show map of the United StatesLocationSuffolk, Massachusetts, U.S.Coordinates42°25′30″N 70°58′58″W / 42.42500°N 70.98278°W / 42.42500; -70.98278[1]Area84 acres (34 ha)[2]Elevation10 ft (3.0 m)[1]Established1896OperatorMassachusetts Department of Conserv...

Infection transmitted through human sexual behavior STD redirects here. For other uses, see STD (disambiguation). Sexually transmitted infections redirects here. For the journal, see Sexually Transmitted Infections (journal). Sexual disease redirects here. Not to be confused with sexual dysfunction. Medical conditionSexually transmitted infectionOther namesSexually transmitted disease (STD);Venereal disease (VD)Condom Museum, BangkokSpecialtyInfectious diseaseSymptomsNone, vaginal discharge, ...

Princeton Chert est une localité en Colombie-Britannique, Canada. Elle présente l'une des collections de plantes fossiles les mieux préservées de l'Éocène dans le monde, avec une particulière abondance et diversité des espèces[1],[2],[3]. Gros plan de l'affleurement du Chert de Princeton montrant des cendres volcaniques (couche blanche à la base), du charbon tourbeux (couche foncée) et des couches de Chert (gris). Le site se trouve sur la rive est de la rivière Similkameen, au sud...

Player selection process This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 2014 WNBA draft – news · newspapers · books · scholar · JSTOR (July 2014) (Learn how and when to remove this message) 2014 WNBA draftGeneral informationSportBasketballDate(s)April 14, 2014LocationMohegan Sun Arena, Uncasville, Connectic...

Legality, use and culture of cannabis in the U.S. state of West Virginia Governor Jim Justice signs the Medical Cannabis Act on April 19, 2017. Cannabis in West Virginia is illegal for recreational use, but partially decriminalized in the city of Morgantown.[1] Possession of small amounts is a misdemeanor crime.[2] Medical use was legalized in 2017 through legislation signed by Governor Jim Justice. Medical cannabis Medical cannabis bills were introduced in West Virginia in ea...

2015 single by One DirectionPerfectSingle by One Directionfrom the album Made in the A.M. Released16 October 2015RecordedJuly 2015Length3:50LabelSycoSonySongwriter(s)Harry StylesLouis TomlinsonJesse ShatkinJacob KasherJohn RyanMaureen Anne McDonaldJulian BunettaProducer(s)Julian BunettaShatkinAFTERHRSOne Direction singles chronology Drag Me Down (2015) Perfect (2015) History (2015) One Direction EP chronology Live While We’re Young EP(2012) Perfect(2015) Music videoPerfect on YouTube Perfe...

St Michael and All Angels Church, Blantyre Mission in Blantyre, Malawi Livingstonia Mission Church According to the 2018 census, 77.3% of the population is Christian. Denominations include Roman Catholics at 17.2% of the total population, Central Africa Presbyterians at 14.2%, Seventh-day Adventist at 9.4%, Anglicans at 2.3%, Pentecostals at 7.6% and other denominations at 26.6%.[1][2] Of the Protestant churches the Church of Central Africa, Presbyterian is one of the largest...


