Dreapta reală
|
Read other articles:

Contea di PanolaconteaContea di Panola – VedutaTribunale della contea LocalizzazioneStato Stati Uniti Stato federato Texas AmministrazioneCapoluogoCarthage Data di istituzione1846 TerritorioCoordinatedel capoluogo32°09′36″N 94°18′36″W / 32.16°N 94.31°W32.16; -94.31 (Contea di Panola)Coordinate: 32°09′36″N 94°18′36″W / 32.16°N 94.31°W32.16; -94.31 (Contea di Panola) Superficie2 127 km² Abitanti23 796 (2010)...

Stefani StoevaInformasi pribadiNama lahirStefani StoevaKebangsaan BulgariaLahir23 September 1995 (umur 28)[1]Galabovo, Bulgaria[1]Tinggi173 m (567 ft 7 in)Tahun aktif2009PeganganKananGanda putriPeringkat tertinggi8 (8 November 2018)Peringkat saat ini10 bersama Gabriela Stoeva (8 November 2022[2])Profil di BWF Stefani Stoeva (bahasa Bulgaria: Стефани Стоева; lahir 23 September 1995) adalah pemain bulu tangkis putri ber...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Mohd Fadhli Mohd Shas – berita · surat kabar · buku · cendekiawan · JSTOR Mohd Fadhli Mohd ShasInformasi pribadiNama lengkap Mohd Fadhli bin Mohd ShasTanggal lahir 21 Januari 1991 (umur 33)Tempat la...

Dia Saba Dia Saba (lahir 18 November 1992) adalah seorang pemain sepak bola Arab-Israel. Ia pernah menjadi bagian dari tim nasional sepak bola Israel dan membela klub Maccabi Haifa di Liga Israel. Ia tercatat pernah membela beberapa klub besar di Turki (Sivasspor), Uni Emirat Arab (Al Nassr) dan Tiongkok (Guangzhou City).[1] Referensi ^ Tak Semua Yahudi, Ini Daftar Pemain Timnas Israel Beragama Islam, Salah Satunya Merupakan Striker Andalan. Detik Sumsel. Artikel bertopik biogra...

Part of the Colombian War of Independence Not to be confused with Siege of Cartagena (1815). Siege of CartagenaPart of the Colombian War of IndependenceDate14 July 1820 – 10 October 1821 (15 months)LocationCartagena de Indias, Viceroyalty of New Granada10°24′N 75°30′W / 10.400°N 75.500°W / 10.400; -75.500Result Gran Colombian victoryBelligerents Gran Colombia Kingdom of SpainCommanders and leaders Mariano MontillaJosé Prudencio Padilla José María Córdova ...

Anbanavan Asaradhavan AdangadhavanPoster filmSutradaraAdhik RavichandranProduserS. Michael RayappanDitulis olehAdhik RavichandranPemeranSilambarasanTamannaahShriya SaranPenata musikYuvan Shankar RajaSinematograferKrishnan VasantPenyuntingRubenPerusahaanproduksiGlobal InfotainmentTanggal rilis 23 Juni 2017 (2017-06-23)[1] Durasi160 menit[2]NegaraIndiaBahasaTamil Anbanavan Asaradhavan Adangadhavan, yang juga dikenal sebagai AAA, adalah sebuah film komedi berbahasa Tam...

Pour l'obchtina de Bulgarie, voir Tchirpan (obchtina). Cet article est une ébauche concernant une localité bulgare. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. TchirpanGalerie-musée Nikola-Manev.GéographiePays BulgarieOblast Stara ZagoraMunicipalité Tchirpan (chef-lieu)Superficie 73,16 km2Altitude 168 mCoordonnées 42° 11′ 53″ N, 25° 19′ 50″ EDémographiePop...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) ألفريدو باي معلومات شخصية الميلاد 27 نوفمبر 1913 تورينو الوفاة يونيو 1980 (66–67 سنة) جيافينو مواطنة إيطاليا (18 يونيو 1946–1 يونيو 1980) مملكة إيطاليا (27 ...

Military figure during the Algerian War Mostéfa MerardaMostéfa Merarda as a teenagerNickname(s)BennouiBornAugust 21, 1928Oued Chaaba, AlgeriaDiedMay 18, 2007Batna (city), AlgeriaAllegianceNational Liberation FrontService/branchNational Liberation ArmyYears of service1954-2007RankCommanding officerCommands heldWilayah IBattles/warsAlgerian WarChildrenSons: Hamid, Ali, Chérif and Abdelmoumen Daughters: Messaouda, Nadia and LeilaSignature Mostéfa Merarda, nicknamed Bennoui, was bo...

State legislative election 2022 Massachusetts Senate election ← 2020 November 8, 2022 2024 → All 40 seats in the Massachusetts Senate21 seats needed for a majorityRegistered4,884,076 [1] ( 1.48 pp)Turnout51.42% ( 24.58 pp) Majority party Minority party Leader Karen Spilka Bruce Tarr Party Democratic Republican Leader since February 28, 2018 January 3, 2011 Leader's seat 2nd Middlesex and Norfolk 1st Essex and Middlesex Last election 3...

Queen of Sweden from 1680 to 1693 For her daughter, see Ulrika Eleonora of Sweden. Ulrika EleonoraPortrait attributed to Jacques d'Agar, 1677Queen consort of SwedenTenure6 May 1680 – 26 July 1693Coronation25 November 1680Born(1656-09-11)11 September 1656CopenhagenDied26 July 1693(1693-07-26) (aged 36)Karlberg PalaceSpouse Charles XI of Sweden (m. 1680)IssueAmong others...Hedvig Sophia, Duchess of Holstein-GottorpCharles XII, King of SwedenUlrika E...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...
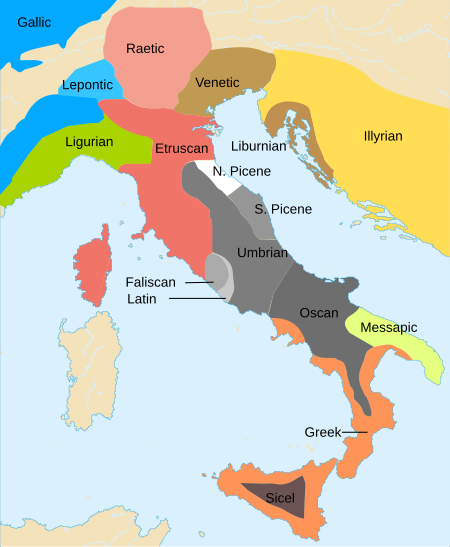
Zaman Besi di Italia Liburnia (bahasa Yunani Kuno: Λιβουρνία)[1] dalam geografi kuno adalah wilayah suku Liburnia, sebuah wilayah di sepanjang pantai Adriatik di Eropa, Kroasia modern, yang perbatasannya bergeser sesuai dengan tingkat dominasi Liburnia pada waktu tertentu antara abad ke-XI dan ke-I SM. Dominasi talasokrasi Liburnia di Laut Adriatik dikonfirmasi oleh beberapa penulis antik,[2][3] tetapi para arkeolog telah mendefinisikan wilayah budaya mate...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Kidman di Festival Film Internasional Berlin 2015 Pemeran Australia Nicole Kidman membuat debut filmnya dalam remake drama Bush Christmas pada 1983.[1][2] Empat tahun kemudian, ia membintangi miniseri televisi Vietnam, yang membuatnya ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Carex brevior Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Monokotil (tanpa takson): Komelinid Ordo: Poales Famili: Cyperaceae Genus: Carex Spesies: Carex brevior Nama binomial Carex brevior(Dewey) Mack. ex Lunell Carex brevior adalah spesies tumbuhan seperti rumput yang tergolong ke dalam famili Cyperaceae. Spesies ini juga merupakan bagian dari ordo Poales. Spesies Carex brevior sendiri merupakan bagian dari genus Carex.[...

Sports associated with Western cultureFor the sports associated with the Western United States, see Western sports (North America).A depiction of the FIFA World Cup, the most popular sporting event in the world. Western sports are sports that are strongly associated with the West.[a] Many modern sports were invented in or standardized by Western countries;[1] in particular, many major sports were invented in the United Kingdom after the Industrial Revolution,[2][3&...

الميديون والفرس على الدرج الشرقي لأبادانا برسيبوليس(الآريیون الإيرانيون القدماء) الآريون أو الآريَّة مصطلح استخدمته الشعوب الهندو إيرانيون في العصور القديمة كتسمية ذاتية، على عكس الشعوب «غير الهندو الآرية» أو «غير الإيرانية».[1] استخدمت الشعوب الإيرانية القديمة مصط...

One of three main historic castes in the Merina Kingdom This article is about a caste among the Merina people in Madagascar. For other uses, see Hova. A Hova man, or free commoner, of the Merina people in 1896. The Hova, or free commoners, were one of the three principal historical castes in the Merina Kingdom of Madagascar, alongside the Andriana (nobles) and Andevo (slaves). The term hova originally applied to all members of a Malagasy clan (possibly of the Zafiraminia people) that migrated...

Itoman 糸満市IchumanKota BenderaLambangLocation of Itoman in Okinawa PrefectureNegara JepangWilayahKyūshūPrefektur OkinawaPemerintahan • WalikotaAkira UeharaLuas • Total46,6 km2 (180 sq mi)Populasi (Oktober 1, 2015) • Total58.547 • Kepadatan1.256/km2 (3,250/sq mi)Zona waktuUTC+9 (Waktu Standar Jepang)Simbol • PohonFicus microcarpa• BungaCatharanthus roseus• IkanLethrinus nebulosusNomor tele...









