Teoria dos crivos
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. AntoniusUskup Eparki Sourozh Jabatan lainEksark Gereja Ortodoks Rusia di Eropa BaratImamatTahbisan imam1948Tahbisan uskup1957Informasi pribadiNama lahirAndrei Borisovich BloomLahir(1914-06-19)19 Juni 1914Lausanne, SwissWafat4 Agustus 2003(2003-08-04) ...

Lumière du jour 13:00 UTC Cet article est une ébauche concernant l’astronomie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. La lumière du jour désigne la lumière naturelle dans la journée. Elle se compose du rayonnement solaire direct, mélangé à la diffusion dans les nuages ou le bleu du ciel. En éclairage, on appelle « lumière du jour » une source lumineuse dont la température de cou...

ZedekiaRaja YehudaBerkuasa597 SM - 586 SMPenobatan22 April 597 SMPendahuluYoyakhinPenerusGedalya (sebagai gubernur yang ditunjuk oleh Nebukadnezar)Kelahiran609 SMYerusalemKematianAgustus 586 SM atau setelahnyaBabelAyahYosia Zedekia (Ibrani: צִדְקִיָּהוּ, Yunani: Ζεδεκίας), yang artinya Kebenaran Tuhan adalah raja kerajaan Yehuda yang terakhir (597-586 SM).[1][2] Ia putra bungsu Yosia, dan dinobatkan oleh Nebukadnezar ketika keponakan laki-lakinya, Yoyakhin,...

Blok M Square - TMLogo Blok M SquareLokasiBlok M, Jakarta Selatan, IndonesiaAlamatJl. Melawai V, Kebayoran Baru, Jakarta Selatan 12160Tanggal dibuka23 Desember 1978 (sebagai Aldiron Plaza)10 Desember 2008 (menjadi Blok M Square)PengembangTrade Mall Agung PodomoroPD Pasar JayaPengurusPT Karya Utama Perdana anggota dari Agung Podomoro GroupPemilikAgung Podomoro GroupTotal luas pertokoan2,12 HaParkir3000 mobilAkses transportasi umumMRT Jakarta: M di stasiun MRT Blok MTransjakarta: 1 4 10 13 (di ...

City in California, United States City in California, United StatesHuron, CaliforniaCityCity of Huron SealLocation of Huron in Fresno County, California.HuronLocation in the United StatesShow map of CaliforniaHuronHuron (the United States)Show map of the United StatesCoordinates: 36°12′10″N 120°06′11″W / 36.20278°N 120.10306°W / 36.20278; -120.10306CountryUnited StatesStateCaliforniaCountyFresnoIncorporatedMay 3, 1951[1]Government • Mayo...

Cet article est une ébauche concernant une compétition de football et l’Italie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Serie A1985-1986 Généralités Sport Football Organisateur(s) FIGC Édition 84e Lieu(x) Italie Date du 8 septembre 1985 au 27 avril 1986 Participants 16 Matchs joués 240 Hiérarchie Hiérarchie 1er échelon Niveau inférieur Serie B 1985-1986 Palmarès Tenant du titre Hellas ...

Genre of Hispanic music, Cuban origins This article is about Cuban genre of song. For the older Spanish dance, see Bolero (Spanish dance). For the composition by Ravel, see Boléro. For other uses, see Bolero (disambiguation). BoleroStylistic originsCuban canciónCultural origins1880s trova from Santiago de CubaDerivative formsBachataFusion genresBolero-sonbolero-chabolero-mamboRegional scenesCubaDominican RepublicMexicoPuerto RicoSpainVietnam Bolero: identity, emotion and poetry turned into ...

Video streaming service VidAngelCompany typePublicIndustryEntertainmentFounded2013; 11 years ago (2013)HeadquartersLehi, Utah, United StatesArea servedUnited StatesKey peopleBill Aho (CEO)ServicesCustom filtering of streaming mediaWebsitevidangel.com VidAngel is an American streaming video company that allows the user to skip objectionable content based on user preferences regarding profanity, nudity, sexual situations, and graphic violence. The company uses customizable fil...
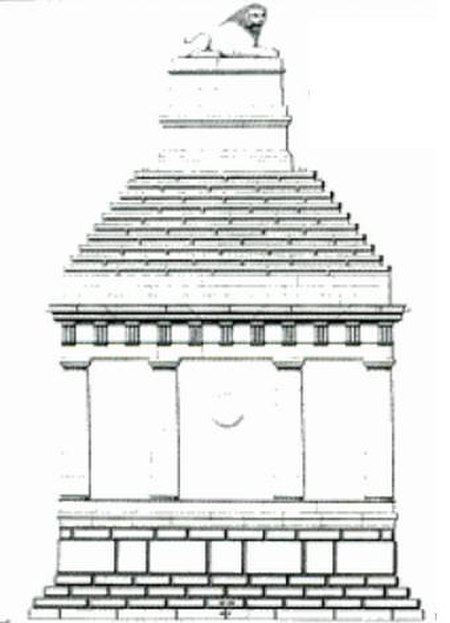
Ancient Greek statue Lion of KnidosLion of KnidosMaterialMarbleSize2.89 m long by 1.82 m highCreatedc. 350–200 BCPresent locationBritish Museum, LondonRegistration1859,1226.24 The Lion of Knidos is the name for a colossal ancient Greek statue erected near the ancient port of Knidos, south-west Asia Minor (now near Datça in Turkey). Although there is some debate about the age of the sculpture, in general, scholarly opinion dates it to the 2nd century BC. Since 2000, it has been promin...

American rock band This article is about the band. For the album, see Taking Back Sunday (album). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Taking Back Sunday – news · newspapers · books · scholar · JSTOR (July 2022) (Learn how and when to remove this message) Taking Back SundayTaking Back Sunday live ...

Gráfico producido por la Oficina Federal de Investigaciones que muestra a los principales jefes de la mafia ítaloestadounidense de todo el país en el año 1963. Las Cinco Familias son las familias criminales principales de la mafia ítaloestadounidense de Nueva York, que han dominado el crimen organizado en la ciudad desde finales del siglo XIX, aunque su poder e influencia se han visto mermados desde comienzos del siglo XXI por las capturas de sus miembros a manos de las autorid...

المملكة المتحدة المملكة المتحدة لبريطانيا العظمى وأيرلندا United Kingdom of Great Britain and Ireland1 1801–1922² المملكة المتحدة لبريطانيا العظمى وأيرلنداعلم المملكة المتحدة المملكة المتحدة لبريطانيا العظمى وأيرلنداشعار المملكة المتحدة الشعار الوطني : الرب وحقي (لغة ...

Le Razos de trobar in un manoscritto catalano Raimon Vidal de Bezaudun(n), in catalano Ramon Vidal de Besalú, in francese Raymond Vidal de Besaudun (1196 – 1252[1]), è stato un trovatore, poeta e grammatico catalano originario di Besalú. Famoso per essere stato l'autore del primo trattato poetico di una lingua romanza (l'occitano), le Razos de trobar (ca. 1210).[2] Indice 1 Biografia 2 Opera 3 Note 4 Bibliografia 5 Voci correlate 6 Altri progetti 7 Collegamenti esterni Bi...

Questa voce è orfana, ovvero priva di collegamenti in entrata da altre voci. Inseriscine almeno uno pertinente e utile e rimuovi l'avviso. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sull'argomento psicologia non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Il paradigma transdi...

Keuskupan JacarezinhoDioecesis IacarezinhoënsisCatedral Nossa Senhora da Conceição e São Sebastião (2016)LokasiNegara BrazilProvinsi gerejawiLondrinaStatistikLuas13.369 km2 (5.162 sq mi)Populasi- Total- Katolik(per 2006)437.000380,000 (87.0%)InformasiRitusRitus LatinPendirian10 Mei 1926 (98 tahun lalu)KatedralCatedral Nossa Senhora da Conceição e São SebastiãoKepemimpinan kiniPausFransiskusUskupFernando José PenteadoEmeritusConrado Walter, S.A...

Architectural structure Saint Petersburg Television TowerСанкт-Петербург Телевизионная башняSaint Petersburg TV Tower as seen from Ushakovskaya EmbankmentLocation within RussiaGeneral informationStatusCompletedTypeSteel lattice television towerLocationSaint Petersburg, RussiaCoordinates59°58′36″N 30°19′15″E / 59.97667°N 30.32083°E / 59.97667; 30.32083Construction started1956Completed1962Opening1963Height326 m (1,07...

Australian physicist and humanitarian Eric BurhopFRSBurhop uses an optical pyrometer to measure the temperature within an apparatusBorn(1911-01-31)31 January 1911Hobart, Tasmania, AustraliaDied22 January 1980(1980-01-22) (aged 68)Camden, London, EnglandAlma materUniversity of MelbourneUniversity of CambridgeAwardsFellow of the Royal Society (1963)Joliot-Curie Medal of Peace (1965)Lenin Peace Prize (1972)Order of Saints Cyril and Methodius (1973)Scientific careerInstitutionsCavendish...

Open Internet standards organization IETF redirects here. For other uses, see IETF (disambiguation). Internet Engineering Task ForceAbbreviationIETF[1]FormationJanuary 14, 1986; 38 years ago (1986-01-14)[2]TypeNon-profitStandards organizationPurposeCreating voluntary standards to maintain and improve the usability and interoperability of the InternetParent organizationInternet SocietyWebsiteietf.org InternetAn Opte Project visualization of routing paths throu...

Зміст 1 Підводні човни побудовані до 1906 1.1 Велика Британія 1.2 Італія 1.3 Російська імперія 1.4 США 1.5 Швеція 1.6 Франція 2 ДПЧ побудовані у 1905—1918 рр 2.1 Велика Британія 2.2 Італія 2.3 Російська імперія 2.4 США 2.5 Німецька імперія 2.6 Швеція 2.7 Франція 3 ДПЧ побудовані у 1919—1945 рр 3.1 В�...

العلاقات النيبالية النيوزيلندية نيبال نيوزيلندا نيبال نيوزيلندا تعديل مصدري - تعديل العلاقات النيبالية النيوزيلندية هي العلاقات الثنائية التي تجمع بين نيبال ونيوزيلندا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين:...


