Teorema fundamental da aritmética
|
Read other articles:

Stadion Sabah Al SalemThe Castle of Cups Informasi stadionNama lengkapStadion Sabah Al SalemPemilikPublic Authority For Youth And SportOperatorAl Arabi KuwaitLokasiLokasi Mansuriyah, Kuwait City , KuwaitKonstruksiDibuat1977Dibuka5 Jan 1979Data teknisPermukaanGrassKapasitas26,000[1]Sunting kotak info • L • BBantuan penggunaan templat ini Sabah al-Salem Stadium Stadium from the outside Al Arabi home ground Stadion Sabah al-Salem adalah sebuah stadion yang berlokasi di Kuwa...

Fuchengmen, 1930. Fuchengmen (Hanzi sederhana: 阜成门; Hanzi tradisional: 阜成門; Pinyin: Fùchéngmén; bahasa Manchu:ᡝᠯᡤᡳᠶᡝᠨ ᡳᠮᡠᡨᡝᡥᡝᡩᡠᡴᠠ;Möllendorf: elgiyen i mutehe duka) adalah sebuah gerbang di sisi barat tembok kota Beijing. Gerbang itu dirobohkan pada 1960-an untuk dijadikan jalan layang Fuchengmen di atas Jalan lingkar ke-2. Stasiun Fuchengmen menjadi simpul transportasi, tempat singgah sejumlah bus umum dan Jalur 2, Beijing Subwa...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Fiskal pajak – berita · surat kabar · buku · cendekiawan · JSTOR Fiskal adalah pajak yang harus dibayar setiap warga Indonesia yang akan berangkat ke luar negeri. Pada tahun 2004, biaya ini sebesar ...

Flüchtlingsandrang vor dem Notaufnahmelager Marienfelde in Berlin, Juli 1961 Flucht aus der Sowjetischen Besatzungszone und der DDR – im Sprachgebrauch der DDR „Republikflucht“ – war das Verlassen der DDR oder ihres Vorläufers, der Sowjetischen Besatzungszone (SBZ), oder Ost-Berlins ohne Genehmigung der Behörden. Von der Gründung der DDR am 7. Oktober 1949 bis in den Juni 1990 verließen über 3,8 Millionen Menschen den Staat, davon viele illegal und unter großer Gefahr...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要补充更多来源。 (2018年3月17日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:羅生門 (電影) — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 �...

Villars-les-Dombes Lambang kebesaranVillars-les-Dombes Lokasi di Region Auvergne-Rhône-Alpes Villars-les-Dombes Koordinat: 45°59′56″N 5°01′48″E / 45.9989°N 5.0299°E / 45.9989; 5.0299NegaraPrancisRegionAuvergne-Rhône-AlpesDepartemenAinArondisemenBourg-en-BresseKantonVillars-les-DombesAntarkomuneCentre DombesPemerintahan • Wali kota (2008–2014) Gabriel HumbertLuas • Land124,63 km2 (951 sq mi) • Populasi24...

Untuk layanan kereta api di Daop 1 Jakarta milik PT Kereta Api Indonesia, lihat Kereta api Cikuray. Gunung CikurayTitik tertinggiKetinggian2.821 m (9.255 kaki)Koordinat7°19′19″S 107°51′35″E / 7.32194°S 107.85972°E / -7.32194; 107.85972Koordinat: 7°19′19″S 107°51′35″E / 7.32194°S 107.85972°E / -7.32194; 107.85972 GeografiGunung Cikuray (tengah) diantara Gunung Papandayan (kiri bawah) dan Gunung Karacak (kanan atas)Le...

Serie B 1933-1934 Competizione Serie B Sport Calcio Edizione 5ª Organizzatore Direttorio Divisioni Superiori Date dal 10 settembre 1933al 24 giugno 1934 Luogo Italia Partecipanti 26 Formula 2 gironi e girone finale Risultati Vincitore Sampierdarenese(1º titolo) Retrocessioni Le retrocessioni sono state tutte annullate:VicenzaSerenissimaCagliariDerthona Statistiche Miglior marcatore Remo Galli (26) Cronologia della competizione 1932-1933 1934-1935 Manuale La Serie B 1933-...

International athletics championship event2015 French Athletics ChampionshipsThe host stadiumDates10–12 JulyHost cityVilleneuve-d'AscqVenueStadium Lille MétropoleEvents38← 2014 2016 → The 2015 French Athletics Championships was the 127th edition of the national championship in outdoor track and field for France. It was held on 10–12 July at the Stadium Lille Métropole in Villeneuve-d'Ascq. A total of 38 events (divided evenly between the sexes) were contested over the three-...

Signature de l'armistice germano-russe du 15 décembre 1917, avec à gauche le commandant des opérations du front de l'Est (maréchal général prince Léopold de Bavière) et à droite la délégation soviétique bolchévique russe (Adolf Joffé, Leo Kamenev et A. Bitsenko, selon la légende de la photo conservée par les archives fédérales allemandes). L'armistice du 15 décembre 1917 est une suspension d'armes entre les Puissances centrales et le pouvoir issu de la révolution d'Octobre...
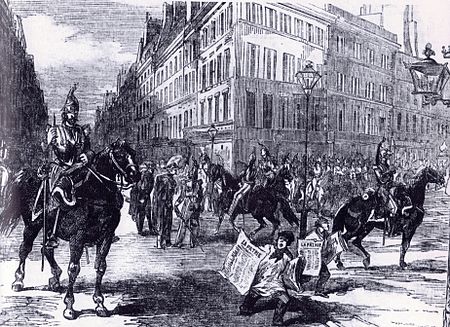
« Golpe » redirige ici. Pour la technique musicale, voir Golpe (guitare). Pour les articles homonymes, voir Coup d'État (homonymie). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mars 2010). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa...

Julius MartovJulius Martov en 1917.BiographieNaissance 24 novembre 1873ConstantinopleDécès 4 avril 1923 (à 49 ans)SchömbergSépulture Urnenfriedhof Gerichtstraße (d)Nom dans la langue maternelle Юлий Осипович МартовNom de naissance Юлий Осипович ЦедербаумNationalité soviétiqueFormation Université d'État de Saint-PétersbourgActivités Homme politique, journaliste d'opinionPère Joseph Alexandrovich Tsederbaum (d)Fratrie Lidiâ Osipovna Dan-...

Johann Caspar Lavater Johann Caspar Lavater (Zurigo, 11 novembre 1741 – Zurigo, 2 gennaio 1801) è stato uno scrittore, filosofo e teologo svizzero. Indice 1 Biografia 2 Gli studi sulla fisiognomica 3 Opere 4 Note 5 Bibliografia 6 Altri progetti 7 Collegamenti esterni Biografia Lavater in una silhouette di W.H. Mewes Pastore protestante di confessione zwingliana, Lavater partecipò attivamente alla vita culturale del suo tempo, sia attraverso i suoi scritti, sia intrattenendo rapporti epist...

Benjamin Nathan Cardozo Hakim Mahkamah Agung Amerika SerikatMasa jabatan14 Maret 1932 – 9 Juli 1938 Informasi pribadiKebangsaanAmerika SerikatProfesiHakimSunting kotak info • L • B Benjamin Nathan Cardozo adalah hakim Mahkamah Agung Amerika Serikat. Ia mulai menjabat sebagai hakim pada mahkamah tersebut pada tanggal 14 Maret 1932. Masa baktinya sebagai hakim berakhir pada tanggal 9 Juli 1938.[1] Referensi ^ Justices 1789 to Present. Washington, D.C.: Mahkamah ...

Pour les articles homonymes, voir La mariée était en noir (roman). La mariée était en noir Données clés Réalisation François Truffaut Scénario François TruffautJean-Louis Richardd'après le roman policier de Cornell Woolrich (alias William Irish) Musique Bernard Herrmann Acteurs principaux Jeanne MoreauMichel BouquetJean-Claude BrialyCharles DennerMichael LonsdaleClaude Rich Sociétés de production Dino De Laurentiis CinematograficaLes Films du CarrosseLes Productions Artistes Ass...

1936 Austrian filmCatherine the LastHans Holt and Franciska GaalDirected byHenry KosterWritten byAlexander Hunyady (novel) Károly Nóti Felix JacksonProduced byJoe PasternakStarringFranciska Gaal Hans Holt Hans Olden Otto WallburgCinematographyTheodore J. PahleEdited byViktor GertlerMusic byNicholas Brodszky Hans J. SalterProductioncompanyUniversal PicturesDistributed byUniversal PicturesRelease date 30 August 1936 (1936-08-30) CountryAustriaLanguageGerman Catherine the Last (...

Legal principle This article is part of a series onPolitics of the European Union Member states (27) Austria Belgium Bulgaria Croatia Cyprus Czech Republic Denmark Estonia Finland France Germany Greece Hungary Ireland Italy Latvia Lithuania Luxembourg Malta Netherlands Poland Portugal Romania Slovakia Slovenia Spain Sweden Candidate countries Albania Bosnia an...

У этого термина существуют и другие значения, см. Горностай (значения). Горностай Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:Челюстнороты...

西維珍尼亞 美國联邦州State of West Virginia 州旗州徽綽號:豪华之州地图中高亮部分为西維珍尼亞坐标:37°10'N-40°40'N, 77°40'W-82°40'W国家 美國加入聯邦1863年6月20日(第35个加入联邦)首府(最大城市)查爾斯頓政府 • 州长(英语:List of Governors of {{{Name}}}]]) • 副州长(英语:List of lieutenant governors of {{{Name}}}]])吉姆·賈斯蒂斯(R)米奇·卡邁克爾(...

Запрос «Дрон» перенаправляется сюда; см. также другие значения. У этого термина существуют и другие значения, см. Беспилотник. Беспилотный летательный аппарат Имя Drone и Drohne Краткое имя/название UAV Названо в честь трутень Создатель Реджинальд Денни[d] Взаимодействуе�...





















































