Matemática pura
|
Read other articles:

Untuk pesepak bola, lihat Aleksandar Ranković (pesepak bola). Aleksandar RankovićАлександар Ранковић Wakil Presiden Yugoslavia ke-1Masa jabatan30 Juni 1963 – 1 Juli 1966PresidenJosip Broz Tito PendahuluJabatan dibentukPenggantiKoča PopovićDeputi Perdana Menteri YugoslaviaMasa jabatan1 April 1949 – 18 April 1963Perdana MenteriJosip Broz Tito PendahuluJaša ProdanovićPenggantiSvetislav StefanovićMenteri Dalam Negeri (Yugoslavia)Masa jabatan2 Feb...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Earl MohanMohan dalam The Fraidy Cat (1924)Lahir12 November 1889 (1889-11-12)Pueblo, Colorado, Amerika SerikatMeninggal15 Oktober 1928(1928-10-15) (umur 38)Los Angeles, California, Amerika SerikatPekerjaanPemeranTahun aktif1915–1927 E...

Japanese light novel and manga series Fate/strange FakeFirst light novel volume cover Light novelWritten byRyōgo NaritaIllustrated byMorii ShizukiPublished byASCII Media WorksImprintDengeki BunkoDemographicMaleOriginal runJanuary 10, 2015 – presentVolumes9 (List of volumes) MangaIllustrated byMorii ShizukiPublished byType-MoonImprintType-Moon BooksDemographicSeinenOriginal runJanuary 10, 2015 – presentVolumes5 (List of volumes) Anime television filmFate/strange F...

Dutch rock band This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: The Gathering band – news · newspapers · books · scholar · JSTOR (October 2017) (Learn how and when to remove this template m...

Peta letak Pulau Giliraja Pulau Gili Raja Gili Raja (Madura: Ghili Rajâ; Péghu: ڬْيلي راجاْ) adalah sebuah pulau kecil yang terletak di sebelah tenggara Pulau Madura. Secara administratif, pulau ini termasuk wilayah kecamatan Giligenting, kabupaten Sumenep, Jawa Timur. Pulau yang indah ini dihuni oleh 14.923 jiwa pada tahun 2015. Sebagian besar masyarakatnya bekerja dalam bidang perikanan tangkap dengan beragam jenis alat tangkap ikan. lbsPulau di Jawa TimurKabupaten Banyuwangi Pu...
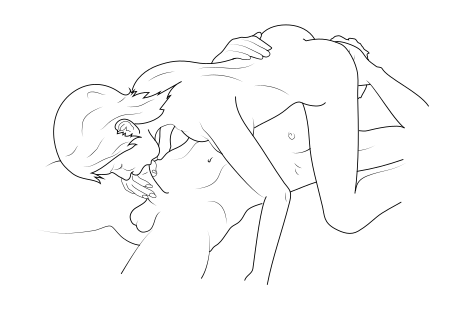
Halaman ini mengandung konten pornografi. Baca Wikipedia: Kebijakan dan pedoman sebelum memulai Wikipedia tidak disensor. Gambar atau rincian yang terdapat dalam artikel ini mungkin bersifat grafis atau tidak pantas demi memastikan kualitas artikel dan liputan lengkap tentang pokok bahasannya. Untuk informasi selengkapnya lihat halaman Wikipedia penyangkalan isi dan opsi untuk tidak melihat gambar. Baca juga: nasihat untuk orang tua. Untuk kegunaan lain, lihat 69. Ilustrasi pasangan yang seda...

Pour les articles homonymes, voir Berzelius. Jöns Jacob BerzeliusBerzelius, d'après Olof Johan Södermark (de), Svenska Familj-Journalen, 1873.FonctionFauteuil 5 de l'Académie suédoise20 décembre 1837 - 7 août 1848Carl von Rosenstein (en)Johan Erik Rydqvist (en)BiographieNaissance 20 août 1779Väversunda (d)Décès 7 août 1848 (à 68 ans)Paroisse Adolphe-Frédéric (d)Sépulture Cimetière de Solna (d)Nationalité suédoiseFormation Université d’UppsalaKatedralskolan (en...

Taren Point Road (ke selatan) menghadap Taren Point. Taren Point Road merupakan sebuah jalan besar yang berada di Taren Point dan Caringbah, New South Wales, Australia. Taren Point Road berawal dari Captain Cook Bridge, Taren Point dan berlanjut ke Gardere Street, Caringbah. Lalu lintas menuju utara mengarah ke Sans Souci, dan ke kota. Lalu lintas menuju selatan mengarah ke Miranda atau Cronulla. Taren Point Road juga berawal atau berakhir di Sutherland Shire Taren Point Road memiliki tiga la...

Tekanan turgor disebabkan kadar air dalam sel tumbuhan yang berlebih Nasti adalah gerak dari bagian tumbuhan yang arahnya tidak bergantung pada arah datangnya rangsangan.[1] Rangsangan akan menyebabkan perubahan tekanan turgor yaitu tekanan air pada dinding sel akibat perubahan kadar air dalam sel tumbuhan sehingga sel menjadi gembung/ tegang.[1][2] Tekanan turgor akan meningkat seiring dengan peningkatan kadar air. Ragam Berdasarkan sumber rangsangannya, gerak nasti d...

Nikolaus Messmer, S.I.vescovo della Chiesa cattolica Incarichi ricoperti Vescovo titolare di Carmeiano (2006-2016) Amministratore apostolico del Kirghizistan (2006-2016) Nato19 dicembre 1954 a Karaganda Ordinato presbitero28 maggio 1989 Nominato vescovo18 marzo 2006 da papa Benedetto XVI Consacrato vescovo2 giugno 2006 dal cardinale Angelo Sodano Deceduto18 luglio 2016 (61 anni) a Biškek Manuale Nikolaus Messmer (Karaganda, 19 dicembre 1954 – Biškek, 18 luglio 2016...

Cet article est une ébauche concernant la musique classique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Consultez la liste des tâches à accomplir en page de discussion. Cymbales antiques Cymbales antiques (en haut à droite) souvent utilisés avec d'autres instruments à percussion, comme le glockenspiel (en bas). Classification Instrument à percussion Famille Idiophones Instruments voisins Glockenspiel...

2014 pro-Russian unrest in UkrainePart of the Russo-Ukrainian WarMap of unrest by region, indicating its peak severityDate23 February – 2 May 2014 (2 months, 1 week and 2 days)LocationEastern and Southern UkraineCaused byOpposition to Euromaidan, success of the Revolution of Dignity and the pro-European outlook of the new government[1][2]Goals Union with Russia[3] Federalization[4] Referendums on status for Eastern Ukraine and Southern Ukraine...

Cet article est une ébauche concernant un homme politique américain. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Dale Bumpers Fonctions Sénateur des États-Unispour l'Arkansas 3 janvier 1975 – 3 janvier 1999(24 ans) Prédécesseur J. William Fulbright Successeur Blanche Lincoln 38e gouverneur de l'Arkansas 12 janvier 1971 – 3 janvier 1975(3 ans, 11 mois et 22 jours) Prédécesseur ...
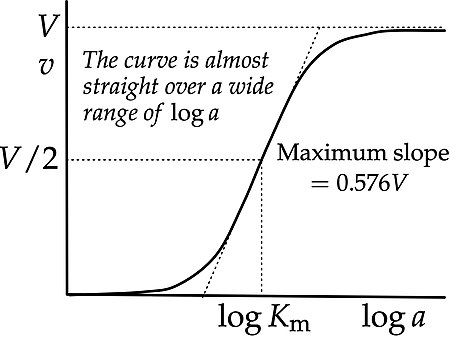
Model of enzyme kinetics Curve of the Michaelis–Menten equation labelled in accordance with IUBMB recommendations In biochemistry, Michaelis–Menten kinetics, named after Leonor Michaelis and Maud Menten, is the simplest case of enzyme kinetics, applied to enzyme-catalysed reactions of one substrate and one product. It takes the form of a differential equation describing the reaction rate v {\displaystyle v} (rate of formation of product P, with concentration p {\displaystyle p} ) to a {\d...

Islam menurut negara Afrika Aljazair Angola Benin Botswana Burkina Faso Burundi Kamerun Tanjung Verde Republik Afrika Tengah Chad Komoro Republik Demokratik Kongo Republik Kongo Djibouti Mesir Guinea Khatulistiwa Eritrea Eswatini Etiopia Gabon Gambia Ghana Guinea Guinea-Bissau Pantai Gading Kenya Lesotho Liberia Libya Madagaskar Malawi Mali Mauritania Mauritius Maroko Mozambik Namibia Niger Nigeria Rwanda Sao Tome dan Principe Senegal Seychelles Sierra Leone Somalia Somaliland Afrika Selatan ...

Department of Public SafetyDepartment overviewHeadquarters1900 E Woodrow Wilson AveJackson, MississippiEmployeesApprox. 1 400 (2021)[1]Annual budgetApprox. $147 000 000[2]Department executiveSean Tindell[3], CommissionerWebsitewww.dps.ms.gov The Mississippi Department of Public Safety is an administrative department of the Government of Mississippi, headquartered in Jackson. It is responsible for the state Highway Patrol and commercial vehicle enforcement; specialized ...

1966 book by Paul Sweezy and Paul A. Baran This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (July 2019) (Learn how and when to remove this message) Monopoly Capital: An Essay on the American Economic and Social Order Cover of the 1967 editionAuthorsPaul Sweezy, Paul A. BaranLanguageEnglishSubjectMonopolyPublisherMonthly Review...

Provinces of the Ottoman Empire Six Vilayets ولايت سته Վեց Հայկական Վիլայեթները Vilayets of Ottoman EmpireThe six Armenian provinces in early 20th century.Today part ofTurkey The Six Vilayets (Ottoman Turkish: ولايت سته, Vilâyat-ı Sitte), the Six Provinces, or the Six Armenian Vilayets (Armenian: Վեց Հայկական Վիլայեթները Vets' haykakan vilayet'nery; Turkish: Altı vilayet, Altı il[1]) were the main Armenian-populated vilay...

Vittorio Benussi Vittorio Benussi (Trieste, 17 gennaio 1878 – Padova, 24 novembre 1927) è stato uno psicologo italiano. Indice 1 Biografia 2 Teoria 3 Influenza 4 Note 5 Bibliografia 6 Voci correlate 7 Altri progetti 8 Collegamenti esterni Biografia Benussi nacque a Trieste nell'Impero austro-ungarico e morì a Padova, in Italia. Trascorse l'infanzia e la giovinezza nella terra natale dove il padre, Bernardo Benussi (1846-1929), istriano, godeva di grande considerazione quale storico e inse...

Province of the Republic of China Yunnan Province雲南省Province of the Republic of China (1912–1951)1912–1951Yunnan Province (red) in the de jure territory of the Republic of ChinaCapitalKunming (1912–1949, de jure)Bangkok, Thailand (in exile) (1950–1951)Area • 1947420,465 km2 (162,342 sq mi)Population • 1947 9,066,000 Historical era20th century• Established 1912• Defection of the Provincial Government 9 December 1949• PRC...
