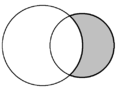
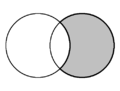
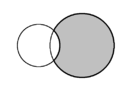
Na geometria plana, a forma crescente formada por dois círculos que se cruzam é chamada de lúnula. Em cada diagrama, duas lúnulas estão presentes e uma é sombreada em cinza.

Em geometria plana, uma lúnula ((latim: luna, «Lua»)^?) é a região côncavo-convexa delimitada por dois arcos circulares.^[1] Ela tem uma porção de limite para a qual o segmento de conexão de quaisquer dois pontos próximos se move para fora da região e outra porção de limite para a qual o segmento de conexão de quaisquer dois pontos próximos fica inteiramente dentro da região. Uma região convexa-convexa é chamada de lente.^[2]

Formalmente, uma lúnula é o complemento relativo de um disco em outro (onde eles se cruzam, mas nenhum é um subconjunto do outro). Alternativamente, se ${\displaystyle A}$ e ${\displaystyle B}$ são discos, então ${\displaystyle A\smallsetminus A\cap B}$ é uma lúnula.

No século 5 aC, Hipócrates de Chios mostrou que a Lúnula de Hipócrates e duas outras lúnulas poderiam ser tornadas quadradas (convertidas em um quadrado com a mesma área) por régua e compasso . Em 1766, o matemático finlandês Daniel Wijnquist, citando Daniel Bernoulli, listou todas as cinco lúnulas quadradas geométricas, somando-se àquelas conhecidas por Hipócrates. Em 1771, Leonard Euler deu uma abordagem geral e conseguiu certa equação para o problema. Em 1933 e 1947 foi provado por Nikolai Chebotaryov e seu aluno Anatoly Dorodnov que essas cinco são as únicas lúnulas quadratáveis.^{[3] [1]}

A área de uma lúnula formada por círculos de raios a e b ( b>a ) com distância c entre seus centros é:^[3]

${\displaystyle A=2\Delta +a^{2}\sec ^{-1}\left({\frac {2ac}{b^{2}-a^{2}-c^{2}}}\right)-b^{2}\sec ^{-1}\left({\frac {2bc}{b^{2}+c^{2}-a^{2}}}\right),}$

onde ${\displaystyle {\text{sec}}^{-1}}$ é a função inversa da função secante, e onde

${\displaystyle \Delta ={\frac {1}{4}}{\sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}}$

é a área de um triângulo de lados a, b e c .

• Arbelos
• Crescente
• Teorema de Gauss-Bonnet
• Lente

• As Cinco Lúnulas Quadradas em MathPages