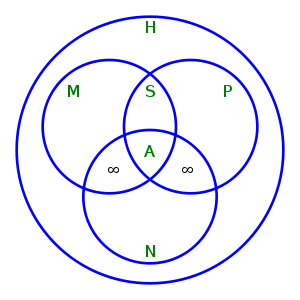
Homomorfismo
|
Read other articles:

Building in New York City, United StatesThe Church of St. JohnGeneral informationArchitectural styleTudor RevivalTown or cityKingsbridge, Bronx, New York CityCountryUnited StatesConstruction started1877 (for first church)[1] 1893 (for present church basement)[1]Completed1877 (for first church)[1]1904 (for present church)[1]Demolished1893 (for removal of first church)[1]Cost$21,000 (for 1893 basement)[1]ClientRoman Catholic Archdiocese of New Yor...

Football League 2018-2019 Competizione Football League Sport Calcio Edizione 60ª Organizzatore EPO Date dal 28 ottobre 2018al 27 maggio 2019 Luogo Grecia Partecipanti 16 Risultati Vincitore Volo(1º titolo) Promozioni VoloPlatanias Retrocessioni ĪraklīsTrikalaĪrodotosAittitos SpataAiginiakosSparta Cronologia della competizione 2017-2018 2019-2020 Manuale La Football League 2018-2019 è stata la 60ª edizione del secondo livello del campionato greco di calcio. Il torneo si �...

Former annual college football event in Miami, Florida Not to be confused with Myrtle Beach Bowl or Florida Beach Bowl. Miami Beach Bowl (defunct) The Battle of the Beach StadiumMarlins ParkLocationMiami, FloridaOperated2014–2016Conference tie-insAmerican Athletic Conference, Conference USA, Mid-American Conference, Sun Belt ConferencePayoutUS$1,000,000 (as of 2015)[1]Succeeded byFrisco Bowl2016 matchupCentral Michigan vs. Tulsa (Tulsa 55–10) The Miami Beach Bowl was a National Co...

2019 American sitcom created by Abby McEnany Work in ProgressOfficial release posterGenreComedyCreated by Abby McEnany Tim Mason Starring Abby McEnany Karin Anglin Celeste Pechous Julia Sweeney Theo Germaine ComposerEthan StollerCountry of originUnited StatesOriginal languageEnglishNo. of seasons2No. of episodes18 (list of episodes)ProductionExecutive producers Abby McEnany Tim Mason Lisa Masseur (pilot) Lilly Wachowski Lawrence Mattis Josh Adler Ashley Berns Julia Sweeney Tony Hernandez Prod...

American boxer (1896–1967) Sam Mosberg or MossbergMosberg in early careerBornSamuel A. MosbergMossberg in 1920's newspapers(1896-06-14)June 14, 1896[1][2]Austria[2] Grew up on New York City's East sideDiedAugust 30, 1967(1967-08-30) (aged 71)[3]Brooklyn, New York[4]NationalityAmericanStatisticsWeight(s)LightweightHeight5 ft 6 in (1.68 m)StanceOrthodox Boxing recordTotal fights29Partial record from BoxRecWins16Includes newspaper win...

Walther von LüttwitzIl generale von Lüttwitz nel 1918NascitaKreuzburg, 2 febbraio 1859 MorteBreslavia, 20 settembre 1942 Dati militariPaese servito Impero tedesco Repubblica di Weimar Forza armata Heer Reichswehr ArmaFanteria GradoGenerale di Fanteria GuerrePrima guerra mondiale voci di militari presenti su Wikipedia Manuale Walther Freiherr von Lüttwitz (Kreuzburg, 2 febbraio 1859 – Breslavia, 20 settembre 1942) è stato un militare tedesco, generale di fanteria. Indice 1 B...

Festival Internacional de Cine de Viña del Mar Cartel Inauguración FICVIÑA 2012Datos básicosNombre oficial Festival Internacional de Cine de Viña del MarOtros nombres FICVIÑATipo InternacionalUbicación Viña del Mar, Chile Primera edición 1962Organizador Departamento de Cinematografía, Ilustre Municipalidad de Viña del MarGalardón PaoaIdioma EspañolEdiciónDirector Juan Esteban MonteroInauguración 1962Página oficial[editar datos en Wikidata] El Festival Internacional d...

24 часа Ле-Мана 2012фр. 24 heures du Mans 47°56′59″ с. ш. 00°12′27″ в. д.HGЯO Дата 16—17 июня 2012 года Место Ле-Ман, Франция Трек Ле-Ман 13,629 км Погода Отчёт Общий заезд Круги 378 (5159,7 км) Поул-позиция Пилот Андре Лоттерер (Audi Sport Team Joest) Время 3:23.787[1] Быстрейший круг...

Крым Общая информация Автор Александр Проханов Тип литературное произведение[вд] Жанр роман Издательство Центрполиграф Год издания 2014 Страниц 382 Тираж 7000 ISBN 978-5-227-05618-4 «Крым» — роман Александра Проханова, журналиста, писателя, главного редактора газет «День» и «Завтр...

第二次世界大戦 > 仏印進駐 仏印進駐Invasion japonaise de l'Indochine 戦争:第二次世界大戦 年月日:1940年9月 - 1941年8月 場所: フランス領インドシナ連邦 結果:日本がフランス領インドシナを制圧し援蒋ルートを遮断、米・英との関係悪化 交戦勢力 大日本帝国 フランス国 フランス領インドシナ連邦 指導者・指揮官 中村明人 西村琢磨 ジャン・ドクー(英語版) 第二�...

L'apprendimento per rinforzo (o reinforcement learning) è una tecnica di apprendimento automatico che punta a realizzare agenti autonomi in grado di scegliere azioni da compiere per il conseguimento di determinati obiettivi tramite interazione con l'ambiente in cui sono immersi. L'apprendimento per rinforzo è uno dei tre paradigmi principali dell'apprendimento automatico, insieme all'apprendimento supervisionato e a quello non supervisionato. A differenza degli altri due, questo paradig...

Incidente aereo del monte VelinoMemoriale sul monte VelinoTipo di eventoIncidente Data8 marzo 1962 Ora23.00 circa TipoGuasto all'altimetro, errore di navigazione LuogoMonte Velino, Rosciolo dei Marsi Stato Italia Coordinate42°08′09.8″N 13°20′28″E42°08′09.8″N, 13°20′28″E Tipo di aeromobileDouglas DC-6 OperatoreSocietà aerea mediterranea Numero di registrazioneI-DIMO PartenzaAeroporto Internazionale di Khartum, Khartum, Sudan DestinazioneAeroporto di Roma-Ciampino, Rom...

أغوسان ديل سور (بالإنجليزية: Province of Agusan del Sur) أغوسان ديل سور خريطة الموقع تاريخ التأسيس 17 يونيو 1967 تقسيم إداري البلد الفلبين [1][2] العاصمة بروسبريداد التقسيم الأعلى كاراجا خصائص جغرافية إحداثيات 8°30′00″N 125°50′00″E / 8.5°N 125.83333333333°E / 8.5; 125.8...

Samarkand Challenger 2008Sport Tennis Data4 agosto - 10 agosto CampioniSingolare Michail Elgin Doppio Irakli Labadze / Denis Macukevič 2007 2009 Il Samarkand Challenger 2008 è stato un torneo di tennis facente parte della categoria ATP Challenger Series nell'ambito dell'ATP Challenger Series 2008. Il torneo si è giocato a Samarcanda in Uzbekistan dal 4 al 10 agosto 2008 su campi in terra rossa e aveva un montepremi di $35 000+H. Indice 1 Vincitori 1.1 Singolare 1.2 Doppio 2 Collegamenti es...

Second wife of Charles Sanders Peirce Juliette Peirce in 1883, the year she married Charles Part of a series onCharles Sanders Peirce Bibliography Pragmatism in epistemology Abductive reasoning Fallibilism Pragmaticism as maxim as theory of truth Community of inquiry Logic Continuous predicate Peirce's law Entitative graph in Qualitative logic Existential graph Functional completeness Logic gate Logic of information Logical graph Logical NOR Second-order logic Trikonic Type-token distinction ...

اليهودية القرائيةالإطارمناطق الخدمة الرملة — أسدود النوع حركات دينية يهودية التنظيمالأجهزة الداخلية قريميين الدين اليهودية تعديل - تعديل مصدري - تعديل ويكي بيانات اليهودية القرائية هي تيار في اليهودية يطلق عليه أيضا القراؤوت، ويُعرف أتباع هذا التيار باسم العنانيين أو ا...

River in Switzerland, Austria and Germany InnRomansh: EnLower Inn valley from Rattenberg castleLocationCountriesSwitzerlandAustriaGermanyCitiesSt. MoritzScuolLandeckInnsbruckWörglKufsteinRosenheimWasserburg am InnMühldorf am InnBraunau am InnSchärdingPassauPhysical characteristicsSource • locationSwiss Alps (Lägh dal Lunghin) • coordinates46°25′00″N 9°40′35″E / 46.41673°N 9.67645°E / 46.41673; 9.67645 R...

Lyndecomune Lynde – Veduta LocalizzazioneStato Francia RegioneAlta Francia Dipartimento Nord ArrondissementDunkerque CantoneHazebrouck TerritorioCoordinate50°43′N 2°25′E50°43′N, 2°25′E (Lynde) Altitudine34 e 72 m s.l.m. Superficie9,07 km² Abitanti684[1] (2009) Densità75,41 ab./km² Altre informazioniCod. postale59173 Fuso orarioUTC+1 Codice INSEE59366 CartografiaLynde Modifica dati su Wikidata · Manuale Lynde è un comune francese di 684...

Questa voce sull'argomento calciatori ungheresi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Máté FenyvesiNazionalità Ungheria Calcio RuoloCentrocampista CarrieraSquadre di club1 1949-1950 Jánoshalmai SE? (?)1950-1953 Kecskemét? (?)1953-1969 Ferencváros343 (84) Nazionale 1954-1966 Ungheria76 (8) Palmarès Europei di calcio BronzoSpagna 1964 1 I due numeri indicano le prese...

Heavy cruiser class of the Italian Royal Navy Trento early in her career Class overview Builders Cantiere navale fratelli Orlando Stabilimento Tecnico Triestino Operators Regia Marina Preceded byNone Succeeded byZara class Built1925–1929 In commission1928–1943 Completed2 Lost2 General characteristics TypeHeavy cruiser DisplacementFull load: 13,334 long tons (13,548 t) Length196.96 m (646 ft 2 in) o/a Beam20.6 m (67 ft 7 in) Draft6.8 m (22&...