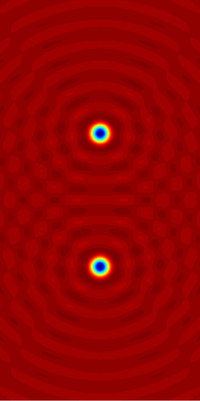
Equação de Helmholtz
|
Read other articles:

Selamat Hasundau artinya selamat datang pada gapura Lawang sakepeng Atraksi Lawang sakepeng yang biasa di tampilkan dalam acara pernikahan ataupun menyambut tamu di Kalimantan Tengah Lawang Sekepeng adalah atraksi silat dari suku Dayak Ngaju dari provinsi Kalimantan Tengah. Lawang artinya pintu atau gapura dan sakepeng berarti satu keping. Lawang sakepeng sering diperagakan pada upacara adat baik untuk menyambut tamu maupun acara perkawinan. Gapura Lawang sakepeng biasanya dibuat dari kayu de...

Christian theologian (c. 339–397) St. Ambrose redirects here. For the university, see St. Ambrose University. For other uses, see Ambrose (disambiguation). SaintAmbrose of MilanBishop of MilanDetail from possibly contemporary mosaic (c. 380–500) of Ambrose in the Basilica of Sant'Ambrogio[1]DioceseMediolanum (Milan)SeeMediolanumInstalled374 ADTerm ended4 April 397PredecessorAuxentiusSuccessorSimplicianOrdersConsecration7 December 374Personal detailsBornAurelius Ambrosiusc.&#...

SukorejoKecamatanNegara IndonesiaProvinsiJawa TengahKabupatenKendalPopulasi • Total57,194(sensus 2.008) jiwaKode Kemendagri33.24.03 Kode BPS3324020 Desa/kelurahan18 Danau Banaran di desa Bringinsari Sukorejo (Jawa: ꦱꦸꦏꦉꦗ, translit. Sukareja) adalah salah satu kecamatan di Kabupaten Kendal, Jawa Tengah, Indonesia. Kecamatan ini terletak di sebelah selatan kabupaten Kendal. Sejarah Kecamatan Sukorejo berdiri sebagai kecamatan definitif tahun 1981 berdasarkan ...

American mathematician (born 1943) This article is about the American mathematician. For other people named Richard Hamilton, see Richard Hamilton. Richard HamiltonHamilton in 1982Born (1943-01-10) January 10, 1943 (age 81)Cincinnati, Ohio, United StatesNationalityAmericanAlma materYale University (BA)Princeton University (PhD)Known forConvergence theorems for Ricci flowDirichlet problem for harmonic maps and harmonic map heat flowEarle–Hamilton fixed-point theoremGage–Hami...
周處除三害The Pig, The Snake and The Pigeon正式版海報基本资料导演黃精甫监制李烈黃江豐動作指導洪昰顥编剧黃精甫主演阮經天袁富華陳以文王淨李李仁謝瓊煖配乐盧律銘林孝親林思妤保卜摄影王金城剪辑黃精甫林雍益制片商一種態度電影股份有限公司片长134分鐘产地 臺灣语言國語粵語台語上映及发行上映日期 2023年10月6日 (2023-10-06)(台灣) 2023年11月2日 (2023-11-02)(香�...

Second issue of The SeerFebruary, 1853. The Seer was an official periodical of the Church of Jesus Christ of Latter-day Saints (LDS Church) which first appeared in 1853 and was published throughout 1854.[1] History After the LDS Church publicly acknowledged that it was teaching and practicing plural marriage at its September 1852 conference, LDS Church president Brigham Young dispatched apostle Orson Pratt to Washington, D.C., where he was asked to publish an apologetic magazine targe...

國立臺南高級商業職業學校國立臺南高級商業職業學校地址臺南市南區健康路一段327號经纬度22°58′52″N 120°12′09″E / 22.981225°N 120.202575°E / 22.981225; 120.202575邮政编码702其它名称National Tainan Commercial Vocational Senior High School类型技術型高級中等學校隶属教育部创办日期1922年 公立臺南商業補習學校学区臺南市南區学校编号06-261-7123教育部學校代碼210408校長黃耀�...

Untuk Gereja Ortodoks paska Konsili Khalsedon dan penganut paham miafisitisme, lihat Gereja Ortodoks Oriental. Gereja Ortodoks TimurOrthódoxi EkklisíaPenggolonganOrtodoks TimurKitab suciAlkitabTeologiTeologi Ortodoks TimurBentukpemerintahanEpiskopalBadanpemerintahanPatriarkPatriark KonstantinopelBartolomeus I dari KonstantinopelPatriark AleksandriaTheodore II dari AleksandriaPatriark AntiokhiaJohn X dari AntiokhiaPatriark YerusalemTeofilos III dari YerusalemWilayahSeluruh DuniaBahasaYunani,...

Berlin Wall Memorial built in 1998 East side of the memorial Gedenkstätte Berliner Mauerclass=notpageimage| Gedenkstätte Berliner Mauer, Berlin The Gedenkstätte Berliner Mauer (Berlin Wall Memorial) commemorates the division of Berlin by the Berlin Wall and the deaths that occurred there. The monument was created in 1998 by the Federal Republic of Germany and the Federal State of Berlin. It is located on Bernauer Straße at the corner of Ackerstraße and includes a Chapel of Reconciliation...

Finnish ski jumper Veikko KankkonenVeikko Kankkonen after winning the normal hill event at the 1964 Winter Olympics in Innsbruck, AustriaPersonal informationBorn5 January 1940 (1940-01-05) (age 84)Sotkamo, FinlandHeight174 cm (5 ft 9 in)Weight75–78 kg (165–172 lb)SportSportSki jumpingClubLahden Hiihtoseura, Lahti Medal record Representing Finland Olympic Games 1964 Innsbruck Individual normal hill 1964 Innsbruck Individual large hill Veikko Kankkon...

Saison 2023-2024 Ligue de hockey junior Maritimes Québec Vainqueur Voltigeurs de Drummondville Nombre d'équipes 18 Nombre de matchs 68 (saison régulière) Saison précédente Saison suivante modifier La saison 2023-2024 est la 55e saison de hockey sur glace de la LHJMQ. La saison régulière voit dix-huit équipes jouer soixante-huit matchs chacune. La saison régulière débute le 22 septembre 2023 et se termine 23 mars 2024 pour laisser place aux séries éliminatoires. Débutée sous l...

Lukisan dari tahun 1728 yang menggambarkan Tabut Perjanjian, beserta perkakas-perkakas lain, pada waktu pendirian Kemah Suci pertama kalinya, sebagaimana dicatat dalam Keluaran 40:17-19 Tabut Perjanjian (Ibrani: אָרוֹן הָבְרִית Ārōn Hāb’rīt [pelafalan modern Aron Habrit]; bahasa Arab: تابوت العهد Tābūt Al-ʿahd; bahasa Inggris: Ark of the Covenant atau Ark of Testimony; juga disebut Tabut Hukum Allah[1] atau Tabut Allah (Ark of God)[2 ...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Human rights in Africa – news · newspapers · books · scholar · JSTOR (April 2009) (Learn how and when to re...

Madura–Kangean Madura Wilayah Kepulauan Kangean Kepulauan Masalembu Pulau Bawean Pulau Madura Pulau Jawa (Tapal Kuda) Etnis Bawean Jawa (sebagian) Kangean Madura Penutur Rumpun bahasaAustronesia Melayu-PolinesiaMelayu-SumbawaMadura–KangeanKangean Madura Bentuk awalProto Madura–Kangean (Bahasa induk) Madura–Kangean Kode bahasaISO 639-3–Glottologmadu1247[1]Linguasfer31-MFLLokasi penuturanWilayah dimana rumpun bahasa Madura–Kangean dituturkan secara dominan (Provinsi Jawa Tim...

Presidente de laJunta General del Principado de Asturias Escudo de Asturias Juan Cofiño González Desde el 26 de junio de 2023Sede Palacio de la Junta GeneralCalle Fruela, 1333007 Oviedo, AsturiasTratamiento Excelentísimo/a señor/aSalario 70.511,12 € anuales[1]Duración 4 años, sin límiteDesignado por Junta General del Principado de AsturiasSuplente Vicepresidentes de la Junta GeneralCreación 6 de marzo de 1982 (42 años)Primer titular Agustín Antuña Alonso (UCD)Sit...

Mexican land grant in present-day Los Angeles and Ventura counties, California Rancho San Francisco1843 map of Rancho San FranciscoLocationNorthwestern Los Angeles County and eastern Ventura County, CaliforniaCoordinates34°26′02″N 118°36′28″W / 34.43389°N 118.60778°W / 34.43389; -118.60778Area48,612 acres (19,673 ha)EstablishedJanuary 22, 1839 California Historical LandmarkOfficial nameRancho San Francisco[1]Reference no.556 California His...

Sloop of the Royal Navy For other ships with the same name, see HMS Enchantress. HMS Enchantress in April 1945 History United Kingdom NameBittern: re-named Enchantress in 1935 BuilderJohn Brown & Company, Clydebank Laid down9 March 1934 Launched21 October 1934 Commissioned8 April 1935 DecommissionedMay 1946 IdentificationPennant number: L56 FateSold for scrap 1952 General characteristics [1] Class and typeBittern-class sloop Displacement1,085 tons Length282 ft (86 m) Bea...

アミラーゼ (amylase)はジアスターゼとも称される、膵液や唾液に含まれる消化酵素。グリコシド結合を加水分解することでデンプン(ラテン語amylum)中のアミロースやアミロペクチンを、単糖類であるグルコースや二糖類であるマルトースおよびオリゴ糖に変換する酵素群である。 概要 アミラーゼは1833年、フランスの生化学者、アンセルム・ペイアン (Anselme Payen) とジャン...
San Luca di MelicuccàIcona di San Luca di Melicuccà presso la chiesa dei Santi Elia e Filarete a Seminara Vescovo NascitaMelicuccà, 1035/1040 MorteAmaroni, 10 dicembre 1114 Venerato daChiesa cattolica Ricorrenza10 dicembre Manuale Luca di Melicuccà, detto Luca il Grammatico (Melicuccà, 1035/1040 – Amaroni, 10 dicembre 1114), fu monaco basiliano e vescovo. Venerato come santo dalla Chiesa cattolica, è ricordato il 10 dicembre. Biografia Nacque a metà dell'XI secolo in provi...

「民俗学」とは異なります。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 民族学 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2016年5月) 成長の儀式(マラウ�...