Classificação dos grupos simples finitos
|
Read other articles:

Jared DiamondLahirJared Mason Diamond10 September 1937 (umur 86)Boston, MassachusettsTempat tinggalAmerika SerikatWarga negaraAmerika SerikatAlmamater Harvard College Universitas Cambridge Penghargaan Phi Beta Kappa Award in Science (1997) Royal Society Prize for Science Books (1992, 1998 & 2006) Pulitzer Prize (1998) National Medal of Science (1999) Karier ilmiahBidang Fisiologi Biofisika Ornitologi Environmentalisme Sejarah Ekologi Geografi Biologi evolusioner Antropologi Institus...

Family of true bugs Not to be confused with Gerreidae. Water skipper redirects here. For the butterfly with this common name, see Parnara monasi. For the tracked vehicle, see Snowmobile skipping. GerridaeTemporal range: Eocene–Recent PreꞒ Ꞓ O S D C P T J K Pg N mating in Cyprus Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Hemiptera Suborder: Heteroptera Superfamily: Gerroidea Family: GerridaeLeach, 1815 Subfamilies[1] Rha...

Soviet and Russian geographer and Antarctic explorer Andrey KapitsaBornAndrey Petrovich KapitsaАндрей Петрович Капица(1931-07-09)9 July 1931Cambridge, EnglandDied2 August 2011(2011-08-02) (aged 80)Moscow, RussiaNationalityRussianCitizenshipRussiaAlma materMSU Faculty of GeographyKnown fordiscovery of the largest subglacial lake in Antarctica, Lake VostokAwardsUSSR State Prize (1971), Dmitry Anuchin Prize (1972), Honorary Scientist of Russia[1][2&...

Strong negative feeling towards a person with leprosy Part of a series onDiscrimination Forms Institutional Structural Statistical Taste-based Attributes Age Caste Class Dialect Disability Genetic Hair texture Height Language Looks Mental disorder Race / Ethnicity Skin color Scientific racism Rank Sex Sexual orientation Species Size Viewpoint Social Arophobia Acephobia Adultism Anti-albinism Anti-autism Anti-homelessness Anti-drug addicts Anti-intellectualism Anti-intersex Anti-left ...

County in New Jersey, United States County in New JerseySomerset CountyCountySomerset County courthouse in Somerville, the county seat FlagSealLocation within the U.S. state of New JerseyNew Jersey's location within the U.S.Coordinates: 40°34′N 74°37′W / 40.56°N 74.61°W / 40.56; -74.61Country United StatesState New JerseyFoundedMay 14, 1688[1]Named forEnglish county of Somerset[2]SeatSomerville[3]Largest municipalityFranklin To...

This article may need to be rewritten to comply with Wikipedia's quality standards. You can help. The talk page may contain suggestions. (April 2013) 2002 video gameState of EmergencyDeveloper(s)VIS EntertainmentPublisher(s)Rockstar Games (PlayStation 2, Xbox)Global Star Software (Windows)Platform(s)PlayStation 2, Xbox, Microsoft WindowsReleasePlayStation 2NA: 12 February 2002EU: 22 February 2002XboxNA: 25 March 2003EU: 4 April 2003Microsoft WindowsEU: 1 August 2003NA: 5 August 2003Genre(s)Be...

Bush TheatreUbicazioneStato Regno Unito LocalitàLondra IndirizzoShepherd's Bush Dati tecniciCapienza180 posti RealizzazioneCostruzioneXX secolo Inaugurazione6 aprile 1972 ProprietarioAlternative Theatre Company Sito ufficiale Modifica dati su Wikidata · Manuale Il Bush Theatre è un teatro londinese sito nel quartiere di Hammersmith e Fulham. Il teatro fu fondato nel 1972 ed è specializzato nella messa in scena di opere di drammaturghi contemporanei ed emergenti. Indice 1 Storia ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目的引用需要清理,使其符合格式。 (2019年8月18日)参考文献应符合正确的引用、脚注及外部链接格式。 此條目使用外部链接的方式可能不符合维基百科的方针或指引,或致使內文成為链接農場。 (2019年8月18日)請協助清理過度與不適當的外部連結,并将有用的链接移到参考文献中。详情请参见条目...

Student newspaper for La Salle University For other uses, see The Collegian (disambiguation). This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Collegian La Salle University – news · newspapers · books · scholar · JSTOR (August 2018) (Learn how and when to remove this message) The CollegianNameplate f...

Disambiguazione – Se stai cercando la definizione di azienda nel diritto italiano, vedi Azienda (ordinamento italiano). Questa voce o sezione sugli argomenti diritto e economia ha un'ottica geograficamente limitata. Contribuisci ad ampliarla o proponi le modifiche in discussione. Se la voce è approfondita, valuta se sia preferibile renderla una voce secondaria, dipendente da una più generale. Segui i suggerimenti dei progetti di riferimento 1, 2. Questa voce o sezione sull'argo...

Mike LaughtonNazionalità Canada Altezza188 cm Peso84 kg Hockey su ghiaccio RuoloCentro Tiro Sinistro Termine carriera1978 Carriera Periodo Squadra PG G A Pt Giovanili 1961-1963 Nelson Knights Squadre di club0 1962-1966 Nelson Maple Leafs 155 96 90 186 1966-1967 Victoria Maple Leafs 62 16 11 27 1967-1970 Oakland Seals 175 40 52 92 1967-1968 → Vancouver Canucks 23 8 5 13 1968-1969 → Cleveland Barons 13 2 6 8 1970-1971 California Golden Seals 25 1 0 ...
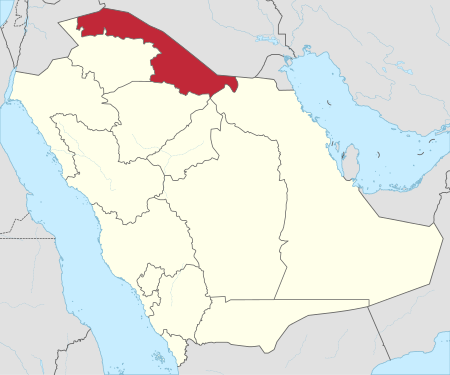
هجوم عرعر 2015 جزء من هجمات داعش في السعودية المعلومات الموقع مركز السويف الحدودي مع العراق ، التابع لقرية جديدة عرعر السعودية التاريخ 5 يناير 2015 الهدف نقطة أمنية حدودية نوع الهجوم إطلاق نار ، تفجير إنتحاري الأسلحة حزام ناسف الخسائر الوفيات 7 ، 3 منهم من رجال الأمن ، و 4 من �...

Pour les articles homonymes, voir Devillers. Gilles DevillersGilles Devillers au Grand Prix Criquielion 2014.InformationsNaissance 12 février 1985 (39 ans)GerpinnesNationalité belgeÉquipes amateurs 2006-2007Storez Ledecq Matériaux2008-2009Pesant Club Liégeois2010Lotto-Bodysol2011Wallonie Bruxelles-Crédit agricole2014Veranclassic-Doltcini2015Ottignies-PerwezÉquipes professionnelles 09.2005-12.2005[n 1]RAGT Semences (stagiaire)2012[n 2]Landbouwkrediet2012[n 3]Landbouwkrediet-Euphon...

水主町延長線概要現況 廃止起終点 起点:水主町電停終点:六反小学校前電停駅数 2駅運営開業 1934年9月11日廃止 1972年3月1日所有者 名古屋市交通局(名古屋市電)路線諸元路線総延長 0.4 km軌間 1,067 mm (3 ft 6 in)電化 直流600 V・架空電車線方式 路線図(1961年) テンプレートを表示 路線概略図 凡例 0.0 水主町電停 ↑岩井町線 ←下江川線→ 0.4 六反小�...

Period in the evolution of the early universe Part of a series onPhysical cosmology Big Bang · Universe Age of the universe Chronology of the universe Early universe Inflation · Nucleosynthesis Backgrounds Gravitational wave (GWB) Microwave (CMB) · Neutrino (CNB) Expansion · Future Hubble's law · Redshift Expansion of the universe FLRW metric · Friedmann equations Inhomogeneous cosmology Future of an expanding universe Ultimate fate of the universe Componen...

遊牧民族のサーミ人 遊牧民(ゆうぼくみん)あるいは遊牧民族(ゆうぼくみんぞく)は、牧畜(遊牧)を生業とする人々や民族を指す。似た概念に移牧民があるが、こちらは季節ごとに移動しても定住地を持つ点が異なる。英語では、ノマド(nomad)がほぼ相当する言葉だが(語源はギリシア語のノマデス νομάδες)、牧畜以外の生業を取る移動型の人々(ジプシー�...

جداول تحويل الوحدات يمكن تحويل الطاقة من صورة إلى أخرى، مثل تحويل طاقة كهربائية إلى طاقة حرارية، وهذا ما يعمله الفرن، وبالتالي توجد علاقات للتحويل بين صور الطاقات المختلفة: الطاقة اسم الوحدة الرمز التعريف العلاقة بوحدات إس آي جول J ≡ m·N == W·s = V·A·s == kg·m²/s² = 1 J= k g ⋅ m 2 s 2 {\dis...

Hamilton Deane (Wexford, 1880 – Ealing, 25 ottobre 1958) è stato un commediografo, scrittore e attore irlandese naturalizzato britannico, celebre per essere stato il primo ad adattare per il teatro il romanzo Dracula di Bram Stoker, nel 1924 a Londra. Indice 1 Dracula a teatro 2 Commedie 3 Filmografia parziale 4 Note 5 Voci correlate 6 Collegamenti esterni Dracula a teatro Hamilton Deane e John L. Balderston sono indicati come autori di una rappresentazione teatrale di Dracula del 1938 in ...

British art historian and curator Arthur Mayger Hind Arthur Mayger Hind (1880–1957) was a British art historian and curator, who usually published as Arthur M. Hind or A. M. Hind. He specialized in old master prints, and was Keeper of the Department of Prints and Drawings at the British Museum until he retired in 1945. Many prints continue to be referred to by the numbers from his catalogue of Italian engravings in the British Museum, a work begun in 1910 and published in expanded form ...

Carlson Park Dr. Paul Carlson Park, or, more commonly, Carlson Park, is a small park located in the Carlson Park neighborhood of Culver City, California. It is linear in shape and intended for passive recreational use, featuring open grassy spaces as well as picnic and barbecue facilities. It is named for Dr. Paul Carlson, a former resident of Culver City whose martyrdom in the Democratic Republic of the Congo in 1964 attracted national attention. In the summer, Culver City Public Theater giv...
