Ação de grupo
|
Read other articles:

Archaeological Ensemble of the Bend of the BoyneSitus Warisan Dunia UNESCOKriteriaBudaya: i, iii, ivNomor identifikasi659Pengukuhan1993 (ke-17) Lorong Timur, Knowth, Co. Meath Knowth (/ˈnaʊθ/; Irlandia: Cnoghbhacode: ga is deprecated ) adalah sebuah lorong batu Neolitikum dan monumen kuno di Brú na Bóinne di desa River Boyne di Irlandia. Knowth adalah lorong batu terbesar yang berada di kompleks Brú na Bóinne. Referensi Byrne, Francis John, Irish Kings and High-Kings. Batsford, Lo...

Bandar Udara HostomelАеропорт «Антонов»Sukhoi Su-27 milik Angkatan Udara Ukraina di Bandar Udara HostomelIATA: GMLICAO: UKKMInformasiJenisPemerintahan sipilPengelolaAntonov AirlinesMelayaniKievLokasiHostomel, Oblast Kiev, UkrainaKetinggian dpl158 mdplKoordinat50°36′13″N 30°11′31″E / 50.60361°N 30.19194°E / 50.60361; 30.19194Koordinat: 50°36′13″N 30°11′31″E / 50.60361°N 30.19194°E / 50.60361; 30....

English writer of Anglo-Norman verse Bibbsworth Hall: the farmhouse (built after Walter's time) Walter of Bibbesworth (1235–1270) was an English knight and Anglo-Norman poet. Documents confirm that he held land in the parish of Kimpton, Hertfordshire at the farm now called Bibbsworth Hall (Bibbs Hall on some maps). About 1250 he served in Gascony under the seneschal Nicholas de Molis in the army of the English king Henry III.[1] In 1270/1271 he is believed to have taken part in the ...

Penghargaan Guldbagge ke-37Tanggal28 Januari 2002TempatSwediaSorotanFilm TerbaikSå vit som en snöPenghargaan terbanyakSå vit som en snö (3)Nominasi terbanyakLeva livet (7)Liputan televisiJaringanSVT1 ← 36 Penghargaan Guldbagge 38 → Acara Penghargaan Guldbagge ke-37, yang dipersembahkan oleh Institut Film Swedia, menghargai film-film Swedia terbaik dari tahun 2001, dan diadakan pada 28 Januari 2002. Så vit som en snö garapan Lars Hermann dipersembahkan dengan pengha...

British comedy-drama television series Fresh MeatGenreComedy dramaCreated by Jesse Armstrong Sam Bain Starring Zawe Ashton Greg McHugh Kimberley Nixon Charlotte Ritchie Joe Thomas Jack Whitehall Jelka van Houten Faye Marsay Robert Webb Tony Gardner Music byChristian HensonCountry of originUnited KingdomOriginal languageEnglishNo. of series4No. of episodes30 (List of episodes)ProductionProduction locationsThe Sharp Project, ManchesterCamera setupSingle-cameraRunning time41 minutesProduction co...

Lalo Schifrin Lalo Schifrin (terlahir sebagai Boris Claudio Schifrin lahir 21 Juni 1932) adalah seorang komponis musikus film, dan pianis Argentina. Ia dikenal di seluruh dunia karena tema lagu acara TV Mission:Impossible dan film musikal lain seperti Dirty Harry, The Rise and Fall of the Third Reich, Mannix, The Fox, Cool Hand Luke, Bullitt, Enter the Dragon, THX 1138, The Four Musketeers, The Big Brawl, The Cincinnati Kid, The Man from U.N.C.L.E., The Amityville Horror, The Osterman Weekend...

Untuk kegunaan lain, lihat May. MayTokoh PokémonMay dalam permainan video Pokémon Omega Ruby dan Alpha Sapphire.PenampilanperdanaPokémon Ruby dan Sapphire (2002)PenciptaSatoshi TajiriDidesainolehKen Sugimori (konsep)Atsuko Nishida (permainan video)Sayuri Ichishi (anime)Pengisi suaraBahasa Jepang:Midori KawanaBahasa Inggris:Veronica Taylor (4Kids)Michelle Knotz (Pokémon USA)InformasiAliasSapphire (manga)Jenis kelaminPerempuanPekerjaanKoordinator PokémonKerabatMax (adik)Norman (ayah)Caroli...

Шалфей обыкновенный Научная классификация Домен:ЭукариотыЦарство:РастенияКлада:Цветковые растенияКлада:ЭвдикотыКлада:СуперастеридыКлада:АстеридыКлада:ЛамиидыПорядок:ЯсноткоцветныеСемейство:ЯснотковыеРод:ШалфейВид:Шалфей обыкновенный Международное научное наз...

Battaglia di Tinchebrayparte dell'invasione della Normandia da parte di Enrico I d'InghilterraMiniatura del Maestro di Bedford della battaglia di Tinchebray (XV secolo).Data28 settembre 1106 LuogoTinchebray, Normandia, Francia EsitoVittoria decisiva di Enrico I SchieramentiDucato di NormandiaRegno d'Inghilterra ComandantiRoberto II di NormandiaGuglielmo di Mortain Roberto II di BellêmeEnrico I d'InghilterraRanulfo di BayeuxRoberto di Beaumont, II conte di LeicesterGuglielmo di Warenne, II co...
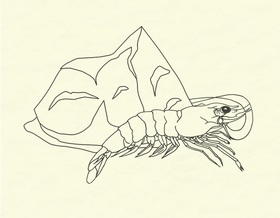
Gambaran peribahasa Ada udang di balik batu. Peribahasa, pepatah, atau amsal adalah kelompok kata yang mempunyai susunan yang tetap dan mengandung aturan berperilaku, nasihat, prinsip hidup, perbandingan atau perumpamaan.[1] Peribahasa biasanya menggunakan kiasan untuk menggambarkan maksud tertentu.[2] Peribahasa adalah salah satu jenis aforisme, yakni suatu bentuk kebahasaan yang ringkas dan berisikan kebenaran umum.[3] Ciri Peribahasa memiliki sejumlah ciri-ciri, di ...

Vous lisez un « bon article » labellisé en 2009. Cette cathédrale n’est pas la seule cathédrale Notre-Dame. Pour les articles homonymes, voir Saint-Privat. CathédraleNotre-Dame-et-Saint-Privatde Mende Présentation Culte Catholique romain Dédicataire Notre Dame et saint Privat Type CathédraleBasilique mineure Rattachement Diocèse de Mende (siège) Début de la construction XIVe siècle Fin des travaux XIXe siècle Style dominant Gothique Protection Class�...

American gymnast Joe KotysKotys in 1949Personal informationFull nameJoseph KotysCountry representedUnited StatesBorn(1925-10-31)October 31, 1925Olyphant, Pennsylvania, U.S.DiedAugust 21, 2012(2012-08-21) (aged 86)Florida, U.S.DisciplineMen's artistic gymnasticsGymSwiss TurnersCollege teamKent State Golden Flashes Medal record Representing United States Men's artistic gymnastics Event 1st 2nd 3rd Pan American Games 2 2 2 Total 2 2 2 Pan American Games 1955 Mexico City...

Spanish politician This biographical article is written like a résumé. Please help improve it by revising it to be neutral and encyclopedic. (February 2010) In this Spanish name, the first or paternal surname is Díaz de Mera and the second or maternal family name is García Consuegra. Agustín Díaz de Mera García ConsuegraDíaz de Mera in 2015Member of the European ParliamentIn office2004–2019ConstituencySpainSenateIn office1996–2004 Personal detailsBorn27 September 1947 ...

لمعانٍ أخرى، طالع حزب البعث العربي الاشتراكي (توضيح). هذه المقالة عن حزب البعث التونسي. لمعانٍ أخرى، طالع حزب البعث (توضيح). حزب البعث العربي الاشتراكي البلد تونس التأسيس التأسيس 1988 تاريخ التأسيس 20 يناير 2011 الشخصيات القادة عثمان بالحاج عمر [1] الأفكار ...

Protein-coding gene in the species Homo sapiens EIF4G3Available structuresPDBOrtholog search: PDBe RCSB List of PDB id codes1HU3IdentifiersAliasesEIF4G3, eIF-4G 3, eIF4G 3, eIF4GII, eukaryotic translation initiation factor 4 gamma 3External IDsOMIM: 603929; MGI: 1923935; HomoloGene: 2789; GeneCards: EIF4G3; OMA:EIF4G3 - orthologsGene location (Human)Chr.Chromosome 1 (human)[1]Band1p36.12Start20,806,292 bp[1]End21,177,285 bp[1]Gene location (Mouse)Chr.Chromosome 4 (mous...

جزء من سلسلة حولالاشتراكية تطورها تاريخ الاشتراكية مناظرة الحساب الاشتراكي اقتصاد اشتراكي أفكار Calculation in kind ملكية جماعية جمعية تعاونية ملكية مشتركة ديمقراطية اقتصادية تخطيط اقتصادي تكافؤ الفرص Free association ديمقراطية صناعية نموذج المدخلات - المخرجات أممية قسيمة العمل تخطيط...

此條目没有列出任何参考或来源。 (2022年2月19日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 2008年夏季奥林匹克运动会马耳他代表團马耳他国旗IOC編碼MLTNOC马耳他奥林匹克委员会網站nocmalta.org(英文)2008年夏季奥林匹克运动会(北京)2008年8月8日至8月24日運動員6參賽項目4个大项旗手Marcon Bezzina...

Limosin yang sering dijumpai Limosin putih yang eksotis Limosin modern yang tidak berbentuk mobil panjang Limosin (kadang-kadang ditulis limusin) (bahasa Inggris: limousine atau limo) adalah kendaraan sedan yang mewah, khususnya dikendarai oleh seorang sopir. Menurut Kamus Besar Bahasa Indonesia, limosin adalah sedan mewah beruang lega, berpintu empat atau lebih, dan ruang penumpang terpisah dari ruang sopir.[1] Beberapa fasilitas keamanan seperti kaca anti-peluru tersedia untuk m...

1917 American filmThe Spirit of RomanceTheatrical release posterDirected byE. Mason HopperScreenplay byAdele HarrisGeorge S. HopkinsStarringVivian MartinPercy ChallengerColin ChaseHerbert StandingElinor HancockGeorge FisherCinematographyJames Van TreesProductioncompanyPallas PicturesDistributed byParamount PicturesRelease date March 22, 1917 (1917-03-22) Running time50 minutesCountryUnited StatesLanguageSilent..English intertitles The Spirit of Romance is a lost[1] 1917...

Dalam nama Korean ini, nama keluarganya adalah Kim. SeolaInformasi latar belakangLahir24 Desember 1994 (umur 29)AsalSeoul, Korea SelatanGenreK-popPekerjaanPenyanyiInstrumenVokalTahun aktif2016-sekarangLabelStarship EntertainmentYuehua EntertainmentArtis terkaitCosmic GirlsStarship Planet Kim Hyun-jung (Hangul: 김현정),[1] yang lebih dikenal sebagai SeolA (설아) (lahir 24 Desember 1994) adalah vokalis utama dari grup vokal perempuan Korea-Tiongkok Cosmic Girls dan anggota uni...