Wyrażenie regularne (ang. regular expression, w skrócie regex lub regexp) – wzorzec opisujący łańcuch symboli. Teoria wyrażeń regularnych jest związana z teorią języków regularnych. Wyrażenia regularne mogą określać zbiór pasujących łańcuchów, jak również wyszczególniać istotne części łańcucha.
W informatyce teoretycznej wyrażenia regularne są ciągami znaków pozwalającymi opisywać języki regularne. W praktyce znalazły bardzo szerokie zastosowanie, pozwalają bowiem w łatwy sposób opisywać wzorce tekstu, natomiast istniejące algorytmy w efektywny sposób określają, czy podany ciąg znaków pasuje do wzorca lub wyszukują w tekście wystąpienia wzorca. Wyrażenia regularne w praktycznych zastosowaniach są zapisywane za pomocą bogatszej i łatwiejszej w użyciu składni niż ta stosowana w rozważaniach teoretycznych. Co więcej, opisane niżej powszechnie wykorzystywane wsteczne referencje (czyli użycie wcześniej dopasowanego fragmentu tekstu jako części wzorca), powodują, że wyrażenie regularne je zawierające może nie definiować języka regularnego.
Wyrażenia regularne stanowią integralną część narzędzi systemowych takich jak sed, grep, wielu edytorów tekstu, języków programowania przetwarzających tekst AWK i Perl, a także są dostępne jako odrębne biblioteki dla wszystkich języków używanych obecnie.
Dwie najpopularniejsze składnie wyrażeń regularnych to składnia uniksowa i składnia perlowa. Składnia perlowa jest znacznie bardziej rozbudowana. Jest ona używana nie tylko w języku Perl, ale także w innych językach programowania: Ruby, bibliotece PCRE do C i w narzędziu powłoki o nazwie pcregrep (znanego też jako pgrep). Perlową składnię stosuje się również w maskach przepisań mod rewrite.
Definicja wyrażeń regularnych
Wyrażeniem regularnym nad alfabetem  nazywamy ciąg znaków składający się z symboli
nazywamy ciąg znaków składający się z symboli  oraz symboli
oraz symboli  z alfabetu
z alfabetu  następującej postaci:
następującej postaci:
 (słowo puste) są wyrażeniami regularnymi;
(słowo puste) są wyrażeniami regularnymi;- wszystkie symbole
 są wyrażeniami regularnymi;
są wyrażeniami regularnymi;
- jeśli
 są wyrażeniami regularnymi, to są nimi również:
są wyrażeniami regularnymi, to są nimi również:
 (domknięcie Kleene’ego)
(domknięcie Kleene’ego) (konkatenacja)
(konkatenacja) (suma)
(suma) (grupowanie)
(grupowanie)
- wszystkie wyrażenia regularne są postaci opisanej w punktach 1–3.
Każde wyrażenie regularne definiuje pewien język formalny. Każdy język definiowany przez wyrażenie regularne jest regularny.
Definicja języka określanego przez wyrażenie regularne
Język definiowany przez wyrażenie regularne jest definiowany indukcyjnie. Niech L(w) oznacza język definiowany przez w. Wtedy baza indukcji jest następująca:
 (zbiór zawierający tylko słowo puste)
(zbiór zawierający tylko słowo puste) (zbiór pusty)
(zbiór pusty) dla dowolnego
dla dowolnego  z alfabetu
z alfabetu
Natomiast do konstrukcji wyrażeń służą 3 symbole:
 (suma języków)
(suma języków) (domknięcie Kleene’ego)
(domknięcie Kleene’ego) (konkatenacja języków)
(konkatenacja języków)
Gwiazdka wiąże najsilniej, konkatenacja słabiej, suma najsłabiej.
Własności wyrażeń regularnych
Wyrażenia są równoważne gdy definiują ten sam język:


 – suma jest przemienna
– suma jest przemienna – łańcuch pusty jest elementem neutralnym konkatenacji
– łańcuch pusty jest elementem neutralnym konkatenacji – suma jest łączna
– suma jest łączna – konkatenacja również jest łączna
– konkatenacja również jest łączna – konkatenacja jest rozdzielna względem sumy
– konkatenacja jest rozdzielna względem sumy

 – domknięcie Kleene’ego jest idempotentne
– domknięcie Kleene’ego jest idempotentne
- Przykład 1
Wyjaśnienie reguł:
 – dowolny ciąg składający się z
– dowolny ciąg składający się z  np.
np. 
 a także pusty
a także pusty – sekwencja, najpierw
– sekwencja, najpierw  następnie
następnie 
 – alternatywa, albo
– alternatywa, albo  albo
albo 
- Przykład 2
Wyrażenie  definiuje język zawierający dokładnie dwa słowa: „Wiki” i „wiki”. To samo można wyrazić wprost
definiuje język zawierający dokładnie dwa słowa: „Wiki” i „wiki”. To samo można wyrazić wprost 
- Przykład 3
Wyrażenie  definiuje język wszystkich słów nad alfabetem
definiuje język wszystkich słów nad alfabetem  które zawierają podsłowo baba.
które zawierają podsłowo baba.
Wyrażenia regularne a automaty skończone
 Ta sekcja jest niekompletna. Jeśli możesz, rozbuduj ją.
Ta sekcja jest niekompletna. Jeśli możesz, rozbuduj ją.Języki regularne można opisać również za pomocą automatów skończonych:
- niedeterministycznego automatu skończonego (NAS) z
 -przejściami (automat może zmienić swój stan bez podania symbolu wejściowego),
-przejściami (automat może zmienić swój stan bez podania symbolu wejściowego),
- niedeterministycznego automatu skończonego bez
 -przejść, oraz
-przejść, oraz
- deterministycznego automatu skończonego (DAS).
| Automat skończony
|
Wyrażenie regularne
|
![]()
|
automat dla pustego języka, nie zawierającego żadnego słowa; 
|
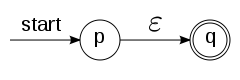
|
automat dla języka akceptującego tylko słowo puste; 
|

|
automat dla języka akceptującego tylko jeden symbol; 
|

|
NAS dla konkatenacji dwóch wyrażeń regularnych: 
|

|
NAS dla sumy dwóch wyrażeń regularnych: 
|

|
NAS dla domknięcia Kleene’ego wyrażenia regularnego: 
|
Jedne z pierwszych praktycznych implementacji wyrażeń regularnych opierały się właśnie na symulacji programowej automatu skończonego. Najpierw budowany jest NAS z  -przejściami zgodnie ze schematem pokazanym wyżej, następnie usuwane są
-przejściami zgodnie ze schematem pokazanym wyżej, następnie usuwane są  -przejścia, kolejnym krokiem jest determinizacja automatu skończonego, czego wynikiem jest otrzymanie DAS, ostatnim zaś etapem jego minimalizacja. Symulowanie DAS jest bardzo proste i szybkie; pierwsze narzędzia systemu Unix używały tej metody, wykorzystuje ją również język AWK, Tcl, a także biblioteki dla języka Haskell.
-przejścia, kolejnym krokiem jest determinizacja automatu skończonego, czego wynikiem jest otrzymanie DAS, ostatnim zaś etapem jego minimalizacja. Symulowanie DAS jest bardzo proste i szybkie; pierwsze narzędzia systemu Unix używały tej metody, wykorzystuje ją również język AWK, Tcl, a także biblioteki dla języka Haskell.
Wyrażenia regularne w praktyce
Porównanie składni praktycznej z teoretyczną
Na początku zostaną pokazane różnice i części wspólne zapisu teoretycznego i praktycznego.
| Informatyka teoretyczna
|
Praktyka
|
Komentarz
|
 |
brak, ""
|
w praktyce zbioru pustego nie podaje się wprost, w większości języków programowania słowo puste jest oznaczane przez "" (parę cudzysłowów)
|

|
(, ) lub \(, \)
|
w niektórych implementacjach symbole specjalne poprzedza się backslashem
|
 |
| lub \|
|
jw.
|

|
[0123abcdefgh] lub krócej [0-3a-h]
|
zakres znaków (dokładny opis – patrz niżej)
|

|
.
|
dowolny znak z alfabetu (tutaj małe i duże litery, w praktyce cały zestaw znaków); w teoretycznym zapisie wymaga wyliczenia wszystkich znaków z alfabetu
|
 |
* lub \*
|
0 lub więcej wystąpień
|
 |
e?
|
wyrażenie e występuje 0 lub 1 raz
|
 |
e+
|
wyrażenie e występuje 1 lub więcej razy
|
| brak |
^
|
metaznak oznaczający początek łańcucha (lub początek wiersza, jeśli przetwarzane są wielowierszowe napisy); w teoretycznych rozważaniach dopasowuje się całe słowa, podczas gdy w praktyce zwykle celem jest znalezienie dopasowania wewnątrz dłuższego tekstu, dlatego dopasowanie do całości wymaga dodatkowych oznaczeń
w zapisie [^e] oznacza negację e
|
| brak |
$
|
metaznak oznaczający koniec łańcucha
|
 |
e{4}
|
określona liczba powtórzeń (tutaj 4); rozszerzenie Perla
|

|
e{4,7}
|
określony zakres liczby powtórzeń wyrażenia e (tutaj od 4 do 7); rozszerzenie Perla
|
Podstawowe elementy
Podstawowe elementy wyrażeń regularnych:
- Każdy znak, oprócz znaków specjalnych, określa sam siebie, np.
a określa łańcuch złożony ze znaku a.
- Kolejne symbole oznaczają, że w łańcuchu muszą wystąpić dokładnie te symbole w dokładnie takiej samej kolejności, np.
ab oznacza że łańcuch musi składać się z litery a poprzedzającej literę b.
- Kropka
. oznacza dowolny znak z wyjątkiem znaku nowego wiersza (zależnie od ustawień i rodzaju wyrażeń).
- Znaki specjalne poprzedzone odwrotnym ukośnikiem
\ powodują, że poprzedzanym znakom nie są nadawane żadne dodatkowe znaczenia i oznaczają same siebie, np. \. oznacza znak kropki (a nie dowolny znak).
- Zestaw znaków między nawiasami kwadratowymi oznacza jeden dowolny znak objęty nawiasami kwadratowymi, np.
[abc] oznacza a, b lub c. Można używać także przedziałów: [a-c]. Między nawiasami kwadratowymi:
- Daszek
^ na początku zestawu oznacza wszystkie znaki oprócz tych z zestawu.
- Aby uniknąć niejasności, znaki
- (łącznik) i ] (zamknięcie nawiasu kwadratowego) zapisywane są na skraju zestawu lub w niektórych systemach po znaku odwrotnego ukośnika, daszek zaś wszędzie z wyjątkiem początku łańcucha. Zasady te mogą być różne w zależności od konkretnej implementacji.
- Większość znaków specjalnych w tym miejscu traci swoje znaczenie.
- Pomiędzy nawiasami okrągłymi
( i ) grupuje się symbole do ich późniejszego wykorzystania.
- Gwiazdka
* po symbolu (nawiasie, pojedynczym znaku) nazywana jest domknięciem Kleene’a i oznacza zero lub więcej wystąpień poprzedzającego wyrażenia.
- Znak zapytania
? po symbolu oznacza najwyżej jedno (być może zero) wystąpienie poprzedzającego wyrażenia.
- Plus
+ po symbolu oznacza co najmniej jedno wystąpienie poprzedzającego go wyrażenia.
- Daszek
^ oznacza początek wiersza, dolar $ oznacza koniec wiersza.
- Pionowa kreska (ang. pipeline)
| to operator OR np., jeśli napiszemy a|b|c, oznacza to, że w danym wyrażeniu może wystąpić a lub b lub c.
- Znaki
\<, \> oznaczające początek i koniec wyrazu (w niektórych implementacjach występuje pełniący podobną funkcję metaznak \b). Np. \<al znajdzie wszystkie wyrazy zaczynające się na al. et\> znajdzie wyrazy które kończą się na et.
- Przykład 1
Polski kod pocztowy składa się z sekwencji następujących elementów:
- dwóch cyfr (
[0-9][0-9]),
- dywizu (
-),
- trzech cyfr (
[0-9][0-9][0-9]).
Ostatecznie wyrażenie regularne, które opisuje kod pocztowy [0-9][0-9]-[0-9][0-9][0-9] lub wykorzystując opisane niżej rozszerzenia perla: [0-9]{2}-[0-9]{3}.
- Przykład 2
Anglosaski napis reprezentujący liczbę rzeczywistą składa się z następujących elementów:
- opcjonalnego znaku (
[+-]?);
- przynajmniej jednej cyfry (
[0-9]+);
- opcjonalnej części ułamkowej (
?), która składa się z kolei z:
- kropki dziesiętnej (
\.);
- przynajmniej jednej cyfry (
[0-9]+).
Wyrażenie regularne opisujące taki napis: [+-]?[0-9]+(\.[0-9]+)?.
- Przykład 3
Wyrażenie sprawdzające poprawność adresów poczty elektronicznej (w wersji uproszczonej, opisujące adresy w najpopularniejszej formie): ^[_a-zA-Z0-9-]+(\.[_a-zA-Z0-9-]+)*@[a-zA-Z0-9-]+(\.[a-zA-Z0-9-]{1,})*\.([a-zA-Z]{2,}){1}$.
Rozszerzenia Perla
Rozszerzenia Perla to między innymi:
- Negacja zestawu (wszystko, co nie należy do zestawu).
- cyfry są zastępowane znakami \d (dowolna cyfra) i \D (wszystko co nie jest cyfrą)
- znaki „białe” \s i \S (przeciwieństwo)
- Rozszerzony zapis przedziałów, wprowadzenie klas znaków np.:
[:digit:] oznacza dowolną cyfrę[:alpha:] literę[:alnum:] literę lub cyfrę
- Możliwość precyzyjnego określenia liczby wystąpień danego wyrażenia
- wyrażenie
{N} oznacza dokładnie N wystąpień
- wyrażenie
{N,} co najmniej N wystąpień wyrażenia
- wyrażenie
{,M} co najwyżej M wystąpień wyrażenia
- wyrażenie
{N,M} od N do M wystąpień wyrażenia
- Referencje wsteczne, czyli możliwość odwoływania się do odnalezionych podciągów zgrupowanych poprzez nawiasy. Np. w wyrażeniu
(.*)\1 referencją wsteczną jest „\1” i oznacza powtórzenie ciągu znalezionego w ramach pierwszej grupy nawiasów. To rozszerzenie pozwala definiować języki, które nie są regularne.
Wyrażenia zachłanne
Kwantyfikatory w wyrażeniach regularnych dopasowują tak wiele znaków, jak to możliwe, są to więc tzw. wyrażenia zachłanne (greedy – z ang. zachłanne, łapczywe). Może to być znaczącym problemem. Przykładowo, aby dopasować pierwszy element, znajdujący się w podwójnych nawiasach kwadratowych w tekście:
- Kolejna eksplozja wieloryba nastąpiła na
[[Tajwan]]ie, [[26 stycznia]] [[1990]].
użytkownik użyłby najchętniej wyrażenia (\[\[.*\]\]), które wygląda poprawnie (nawias kwadratowy powinien być interpretowany jako znak, dlatego poprzedzony jest odwrotnym ukośnikiem), jednak zwróci ciąg [[Tajwan]]ie, [[26 stycznia]] [[1990]] zamiast oczekiwanego [[Tajwan]].
Są dwie metody na uniknięcie tego problemu. Po pierwsze, zamiast określać, co powinno być dopasowane, można określić, co nie powinno być dopasowane. W tym przypadku ] jest znakiem niepożądanym, więc wyrażenie miałoby postać (\[\[[^\]]*\]\]). Jednak nie uda się w ten sposób dopasować ciągu znaków w postaci:
- A B C D E F G
Drugą, bardziej współczesną metodą, jest „zmuszenie” kwantyfikatora, aby nie był typu „greedy”, poprzez dopisanie za nim znaku zapytania (\[\[.*?\]\]). Są to tak zwane „leniwe” (ang. lazy) odmiany kwantyfikatorów.
Wady wyrażeń regularnych
Wyrażenia regularne obecnie nie wspierają[1] obsługi permutacji (wedle obecnych definicji i implementacji), tzn. nie ma mechanizmu, który w zwięzły sposób pozwoliłby dopasować np. ciągi znaków „ABC”, „ACB”, „BAC”, „BCA”, „CAB” i „CBA” (potrzebne jest explicite dopasowanie poszczególnych ciągów)
Zobacz też
Przypisy
Bibliografia
- Jeffrey E.F. Friedl: Wyrażenia regularne. Gliwice: Helion O'Reilly, 2001. ISBN 83-7197-351-9. (pol.). Brak numerów stron w książce
- Tony Stubblebine: Wyrażenia regularne leksykon kieszonkowy Wydanie I. Gliwice: Helion O'Reilly, 12 2003. ISBN 83-7361-075-8. Brak numerów stron w książce
- Tony Stubblebine: Wyrażenia regularne leksykon kieszonkowy Wydanie II. Gliwice: Helion O'Reilly, 01 2008. ISBN 978-83-246-1392-2. Brak numerów stron w książce
- Hopcroft, John E; Ullman, Jeffrey D; Konikowska, Beata: Wprowadzenie do teorii automatów, języków i obliczeń. Warszawa: Wydawnictwo Naukowe PWN, 2003. ISBN 83-01-14090-9. Brak numerów stron w książce
Linki zewnętrzne