Operator liczby cząstek
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Biskuit mentega Biskuit mentega (Inggris: butter cookiescode: en is deprecated ) adalah adalah kue yang dibuat tanpa menggunakan ragi atau pengembang, dengan bahan-bahan mentega, tepung terigu dan gula. Biskuit mentega dikategorikan sebagai biskuit re...

ريال مدريدموسم 2021–22لاعبو ريال مدريد يحتفلون بالثنائية في اليوم التالي من فوزهم بدوري الأبطالالرئيسفلورنتينو بيريزالمدير الفنيكارلو أنشيلوتيالملعبسانتياغو برنابيوالدوري الإسبانيالأولكأس ملك إسبانيادور ربع النهائيكأس السوبر الإسبانيالبطلدوري الأبطالالبطلالهدافال�...

United States Navy Fire Controlman (FC), USN rating badge. Radar pengendali tembakan (Inggris: Fire-control radarcode: en is deprecated (FCR)) adalah radar yang dirancang khusus untuk memberikan informasi (terutama menargetkan azimuth, elevasi, jangkauan dan kecepatan) ke fire-control system untuk menghitung solusi menembak (yaitu informasi tentang bagaimana untuk mengarahkan senjata tersebut ke arah target). Radar tersebut biasanya memancarkan gelombang radio sempit, balok intens untuk memas...

South Korean boyband BigBangBigBang in 2012L-R: G-Dragon, Taeyang, and DaesungBackground informationOriginSeoul, South KoreaGenresK-popJ-pophip hopdanceelectronicR&B[1]Years active2006–20182022LabelsYGUniversal JYGEXWarner TaiwanSpinoffsGD & TOPGD X TaeyangMembers Taeyang G-Dragon Daesung Past members T.O.P Seungri Websitewww.ygbigbang.com[dead link] BigBang (Korean: 빅뱅; stylized in all caps) is a South Korean boy band formed by YG Entertainment. The gro...

This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (June 2018) (Learn how and when to remove this template message) Frost School of MusicAddress1314 Miller DriveCoral Gables, Florida, U.S.InformationSchool typePrivateEstablished1926DeanShelly BergEnrollment716Websitehttps...

Ernest Gruening Senator Amerika Serikat dari AlaskaMasa jabatan3 Januari 1959 – 3 Januari 1969 PendahuluKursi dibentukPenggantiMike GravelGubernur Teritorial Alaska ke-7Masa jabatan6 Desember 1939 – 10 April 1953WakilBob Bartlett PendahuluJohn TroyPenggantiFrank Heintzleman Informasi pribadiLahirErnest Henry Gruening(1887-02-06)6 Februari 1887New York City, New York, Amerika SerikatMeninggal26 Juni 1974(1974-06-26) (umur 87)Washington, D.C., Amerika SerikatPartai po...

English sculptor and painter Alfred Adrian JonesBorn9 February 1845Ludlow, Shropshire, EnglandDied24 January 1938(1938-01-24) (aged 92)Chelsea, LondonNationalityBritishAlma materRoyal Veterinary CollegeKnown forSculptureNotable workPeace descending on the Quadriga of War Alfred Adrian Jones MVO (9 February 1845 – 24 January 1938) was an English sculptor and painter who specialized in depicting animals, particularly horses.[1] Before becoming a full-time artist he was ...

Cet article est une ébauche concernant l’océan Pacifique et les Philippines. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Ciel tropical dans le nord du golfe. Le golfe de Leyte est un golfe des Philippines situé à l'est de l'île de Leyte et ouvrant sur la mer des Philippines (10° 50′ N, 125° 25′ E). Le golfe est bordé au nord par l'île de Samar, qui n'est séparée de Leyte ...

2007 Kuomintang chairmanship by-election ← 2005 7 April 2007 2009 → Turnout53.75% Nominee Wu Po-hsiung Hung Hsiu-chu Popular vote 156,499 23,447 Percentage 86.97% 13.03% Chairman before election Chiang Pin-kung (acting) Elected Chairman Wu Po-hsiung The 2007 Kuomintang chairmanship by-election (Chinese: 2007年中國國民黨主席補選) was held on 7 April 2007 in Taiwan between Wu Po-hsiung and Hung Hsiu-chu. This was the third direct election of the c...

2002 nuclear disarmament treaty between the U.S. and Russia Not to be confused with Strategic Arms Reduction Treaty or Strategic Arms Limitation Talks. SORT redirects here. For other uses, see SORT (disambiguation). SORT / Treaty of MoscowTreaty on Strategic Offensive ReductionsPresidents Vladimir Putin and George W. Bush sign SORT on 24 May 2002 in MoscowTypeStrategic nuclear disarmamentSigned24 May 2002LocationMoscowEffective1 June 2003ConditionRatification of both partiesExpiration5 Februa...

Louis-Michel le Peletier de Saint-Fargeau ritratto da Garneray. Louis-Michel le Peletier, marchese di Saint-Fargeau (anche con la grafia Lepeletier o Lepelletier; Parigi, 29 maggio 1760 – Parigi, 20 gennaio 1793), è stato un politico e rivoluzionario francese. La firma di Louis-Michel le Peletier de Sait-Fargeau nel 1789. Dopo l'abolizione dei titoli nobiliari da parte dell'Assemblea Costituente nel 1790, egli cominciò a firmarsi con solo nome e cognome, come Michel Lepeletier.[1]...

この項目では、有理数 1/7 について説明しています。日米式の月日については「1月7日」を、欧州式の月日については「7月1日」をご覧ください。 この項目には、一部のコンピュータや閲覧ソフトで表示できない文字(Unicode5.2で表現したARIB外字)が含まれています(詳細)。 1/7(7分の1、ななぶんのいち、しちぶんのいち)は、0 と 1 の間にある有理数である。 1⁄7=...

Parts of this article (those related to the lead and statistics) need to be updated. Please help update this article to reflect recent events or newly available information. (October 2020) COVID-19 pandemic in New JerseyDiseaseCOVID-19Virus strainSARS-CoV-2LocationNew Jersey, U.S.First outbreakWuhan, Hubei, ChinaIndex caseBergen CountyArrival dateMarch 2, 2020Confirmed cases2,602,776Deaths34,290Government websitecovid19.nj.gov The COVID-19 pandemic reached the U.S. state of New Jersey with t...

شدة المجال المغناطيسيمعلومات عامةصنف فرعي من كمية فيزيائيةكمية فيزيائية متجهةشدة مجال جزء من مغناطيسيةسكونيات مغناطيسية جانب من جوانب حقل مغناطيسي سُمِّي باسم هانز أورستد البعد حسب النظام الدولي للكميات L − 1 I {\displaystyle {\mathsf {L}}^{-1}{\mathsf {I}}} تعريف الصيغة H = B μ 0 − M {\dis...

Questa voce o sezione sull'argomento pittori svedesi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Alexander Roslin, Autoritratto, 1790, Malmö, Konstmuseum Alexander Roslin (Malmö, 15 luglio 1718 – Parigi, 5 luglio 1793) è stato un pittore svedese, noto soprattutto come ritrattista. Indice 1 Biografia 1.1 I primi anni e l'inizio della carriera 1.2...

Les SSP cartographiés dans l'espace des défis à l'atténuation/adaptation Les trajectoires socio-économiques partagées (en anglais, shared socioeconomic pathways ; SSP) sont des scénarios d'évolutions socio-économiques mondiales projetés jusqu'en 2100. Ils sont utilisés pour élaborer des scénarios d'émissions de gaz à effet de serre associés à différentes politiques climatiques[1]. Concentrations atmosphériques de CO₂ par SSP au cours du XXIe siècle (projetées...

Untitled (Sculpture by Krol)Year1973 (1973)TypePainted metalDimensions290 cm × 200 cm × 370 cm (114 in × 78 in × 144 in)LocationPickwick Farms, Indianapolis, IndianaCoordinates39°55′24″N 86°11′13″W / 39.92333°N 86.18694°W / 39.92333; -86.18694OwnerPickwick Farms Untitled (Krol) is a public artwork by American artist Ronald W. Krol. It is located on the grounds of Pickwick Farms, ...

STS-115Emblema missione Dati della missioneOperatoreNASA NSSDC ID2006-036A SCN29391 VettoreSpace Shuttle Lancio9 settembre 2006, 15:14:55 UTC Luogo lancioRampa 39B Atterraggio21 settembre 2006, 10:21:30 UTC Sito atterraggioShuttle Landing Facility (pista 33) Durata11 giorni, 19 ore e 6 minuti Proprietà del veicolo spazialePeso al lancio2 000 t CaricoP3/P4 arrays della Stazione spaziale internazionale Parametri orbitaliOrbitaorbita terrestre bassa Numero orbite187 Apoapside226.6 km Peria...

この記事は「旧馬齢表記」が採用されており、国際的な表記法や2001年以降の日本国内の表記とは異なっています。 詳しくは馬齢#日本における馬齢表記を参照してください。 メジロアルダン欧字表記 Mejiro Ardan[1]品種 サラブレッド[1]性別 牡[1]毛色 黒鹿毛[1]生誕 1985年3月28日[1]死没 2002年6月18日(17歳没)[2]父 アスワン[1]母 メジ�...
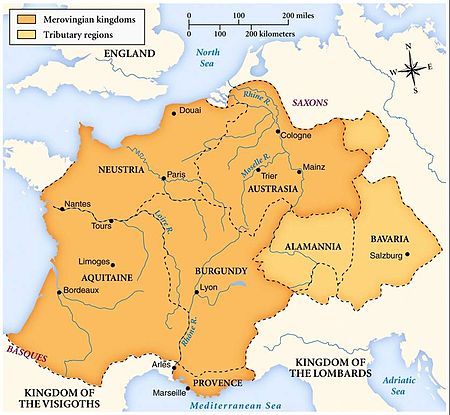
Frankish aristocratic family that ruled from around the middle of the 5th century to 751 Merovingian redirects here. For other uses, see Merovingian (disambiguation). Merovingian Kingdomsc. 481–751History • Established c. 481• Disestablished 751 The Merovingian dynasty (/ˌmɛrəˈvɪndʒiən/) was the ruling family of the Franks from around the middle of the 5th century until 751.[1] They first appear as Kings of the Franks in the Roman army of northern Gaul. By ...












