Lewis Fry Richardson (11. oktober 1881–30. september 1953) var ein engelsk matematikar, fysikar, meteorolog, psykolog og pasifist. Han var ein føregangsmann innan numerisk vêrvarsling, og for nytta av liknande teknikkar i studiet av årsakene til krigar og korleis dei kan førebyggjast. Han er òg kjent for pionerarbeidet sitt innan fraktalar og for ein metode for å løysa lineære likningssystem.[1]
Familie og utdanning
Lewis Fry Richardson var den yngste av sju born av foreldra Catherine Fry (1838–1919) og David Richardson (1835–1913).[2] Dei var ein velståande kvekarfamilie, og David Richardson dreiv ei framgangsrik verksemd innan garveri- og lêrbransjen.[3]
Då han var tolv vart han send til Bootham skule i York, ein internatskule for kvekarar, der han fekk ei utmerka utdanning innan vitskap, noko som stimulerte ei aktiv interesse for naturhistorie. I 1898 fortsette han til Durham College of Science (no Universitetet i Newcastle) der han studerte matematisk fysikk, kjemi, botanikk og zoologi. To år seinare fekk han eit stipendiat til King's College i Cambridge, der han vart uteksaminert med toppkarakterar innan naturvitskap i 1903.[3]
I 1909 gifta han seg med Dorothy Garnett (1885–1956), dotter av matematikaren og fysikaren William Garnett.[4] På grunn av inkompatible blodtypar kunne dei ikkje få barn, men dei adopterte to søner og ei dotter mellom 1920 og 1927.[2]
Karriere
Yrkeskarriere til Richardson reflekterer dei ueinsarta interessene hans:[5]
I 1926 vart han vald inn som medlem av Royal Society[6]
Vêrvarsling
Som matematikar og fysikar vigde han seg til spurnaden om i kva grad ein kunne lage meteorologiske varsel ved hjelp av matematiske modellar basert på differensiallikningar. Med dette for auge utvikla han metodar som i nyare tid har fått stor tyding ved simulering av komplekse fenomen ved hjelp av parallell datahandsaming. Ved dette blir området der hendinga finn stad inndelt i fleire mindre seksjonar, og ideen er å rekne ut tilstanden til kvar seksjon gjennom ein enkel modell. I neste steg blir så resultata frå dei einskilde seksjonane sett i samanheng med resultatet frå naboseksjonane. På denne måten blir det svært komplekse simuleringsproblemet delt opp i ei mengd mindre problem, som i stor grad kan løysast sjølvstendig av kvarandre. I dag blir utrekningane gjort med datamaskinar, men dette var ikkje tilgjengeleg då Richardson i 1922 publiserte Weather Prediction by Numerical Process, og sjølv relativt enkle simuleringar ville ha kravd mange personar som arbeidde med papir og blyant.
Han var òg interessert i atmosfærisk turbulens og utførte mange eksperiment innan dette feltet. Richardson-talet, ein dimensjonslaust parameter innan turbulensteori, er kalla opp etter han.
Pasifisme
Kvekartrua til Richardson medførte ein lidenskapeleg pasifisme, som fritok han frå militærteneste under første verdskrigen som militærnektar, sjølv om dette òg diskvalifiserte han frå å inneha akademiske embete for framtida. Richardson arbeidde frå 1916 til 1919 for ei frivillig ambulanseteneste av kvekarar (Friends' Ambulance Unit) tilknytt 16. franske infanteridivisjon.
I 1920 vart det meteorologiske instituttet (Met Office) han arbeidde for underlagt det britiske Air Ministry (som kontrollerte Royal Air Force). Han vart like etter kontakta av militære representantar, som ynskte å bruke dei meteorologiske modellane hans i samband med spreiing av giftgass i atmosfæren. Richardson nekta, sa opp stillinga si, og avslutta alt arbeid innan dette feltet og øydela resultat som han enno ikkje hadde publisert.[7]
Etter dette heldt han fram med ein karriere i utkanten av den akademiske verda, før han i 1940 trekte seg tilbake for å utforske sine egne idear.
Matematisk analyse av krig
Richardson nytta òg sine matematiske evner i teneste for sine pasifistiske prinsipp, spesielt innan studium av årsakene til internasjonale konfliktar. Av denne grunnen blir han i dag rekna som ein av grunnleggjarane (saman med Quincy Wright og Pitirim Sorokin, og dessutan andre som Kenneth Boulding, Anatol Rapaport og Adam Curle) av vitskapleg konfliktanalyse; eit interdisiplinært felt innan kvantitativ og matematisk sosial vitskap, tileigna til systematisk undersøking av årsakene til krig og vilkår for fred. Som han hadde gjort med vêret analyserte han krig hovudsakleg gjennom bruk av differensiallikningar og sannsynsteori. Når han vurderte væpnaden av to statar rekna Richardson eit idealisert system av likningar der auken av våpenmakta til ein stat er direkte proporsjonalt med våpenmengda som rivalen har, samt med kor sterkt stridsspørsmåla ovanfor rivalen kjennest, og negativt proporsjonalt med mengda av våpen som staten sjølv alt har. Løysinga av dette systemet av likningar gjer det mogleg å trekkje innsiktsfulle konklusjonar vedrørande karakteren og stabiliteten (eller ustabiliteten), til ulike hypotetiske vilkår som kan oppstå mellom statar.
I Arms and Insecurity (1949), og Statistics of Deadly Quarrels (1950), søkte han å statistisk analysere årsakene til krig. Faktorar han vurderte var blant anna økonomi, språk og religion. I forordet til den siste boka skreiv han: «Det føregår i verda mykje brilliant, intelligent politisk diskusjon som ikkje fører til nokre faste løysingar. Siktemålet mitt har vore eit anna: nemleg å undersøkja nokre førestillingar ved hjelp av kvantitative teknikkar i voner om å kome fram til eit påliteleg svar.»
Forsking om lengda på kystlinjer og grenser
Under studia sine av årsakene til krig mellom to land, avgjorde Richardson seg for å undersøkja i kva grad det var ein samanheng mellom sannsynet for at to land skulle gå til krig, og lengda på den felles grensa deira. Medan han samla inn data, innsåg han at det var stor variasjon i dei oppgjevne lengdene på internasjonale grenser i dei ulike kjeldene. Til dømes var grensa mellom Spania og Portugal oppgjeve å vere anten 987 eller 1214 km, og grensa mellom Nederland og Belgia anten 380 eller 449 km.[8]
Som ein del av forskingsarbeidet sitt undersøkte Richardson korleis den oppmålte lengda på ei grense endrast når måleeininga endrast. Han publiserte empirisk statistikk som indikerte ein anteken samanheng. Dette forskingsarbeidet vart sitert av matematikaren Benoît Mandelbrot i avhandlinga hans frå 1967: How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension.
Tenk at kysten av Storbritannia blir mælt med ein 200 km lang linjal, under føresetnad at begge endane av linjalen må røre kysten. Kutt no linjalen i to og gjenta målinga, og gjenta deretter ein gong til:


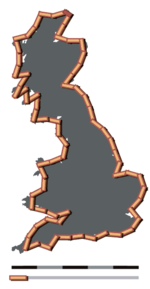
Legg merke til at desto kortare linjalen er, desto lengre blir resultatet. Det kunne teknast at desse verdiane ville konvergere til eit endeleg tal som uttrykte den «eigenlege» lengda til kysten. Richardson viste likevel at den oppmålte lengda til kystlinjer og andre naturlege former ser ut til å auke utan grense etterkvart som måleeininga vert gjort mindre.[9] Dette er i dag kjent som Richardson-effekten.[10]
På den tida vart forskinga til Richardson ignorert av den vitskaplege verda. I dag blir han imidlertid sett på som eit element i framveksten i studiet av fraktalar.
Patent for oppdaging av isfjell
I april 1912, kort tid etter forliset til RMS «Titanic» etter samanstøyt med isfjell, tok Richardson patent for ein måte å oppdaga isfjell på ved hjelp av ekkolokalisering i luft. Ein månad seinare tok han eit liknande patent på ekkolokalisering i vatn, ein forløpar for Paul Langevin og Robert Boyle si utvikling av sonar 6 år seinare.[11]
Bibliografi
(ufullstendig)
- Richardson, L.F. Weather Prediction by Numerical Process. (1922)
- Richardson, L.F. «Generalized foreign politics». (1939), The British Journal of Psychology, monograph supplement #23.
- Richardson, L.F. Statistics of deadly quarrels. (1960), Pacific Grove, CA: Boxwood Press.
- Richardson, L F. The Collected Papers of Lewis Fry Richardson. (1993), (red: Ashford, Oliver M; Charnock H; Drazin, P G; Hunt, J C R; Smoker, P, Sutherland, Ian)
- Vol. 1: Meteorology and numerical analysis (ISBN 978-0521382977, 1030pp.)
- Vol. 2: Quantitative psychology and studies of conflict. (ISBN 978-0521382984, 778pp.), Cambridge University Press, Cambridge.
Kjelder
- ↑ O’Connor, John og Robertson, Edmund F. «Lewis Fry Richardson». MacTutor History of Mathematics archive. Universitetet i St. Andrews.
- ↑ 2,0 2,1 Ashford, Oliver M. (2004). «Richardson, Lewis Fry (1881–1953)». Oxford Dictionary of National Biography. doi:10.1093/ref:odnb/35739. Henta 1. september 2011.
- ↑ 3,0 3,1 Hunt, J.C.R. (1998). «Lewis Fry Richardson and His Contributions to Mathematics, Meteorology, and Models of Conflict» (PDF). Annual Review of Fluid Mechanics 30: xiii–xxxvi. Arkivert frå originalen (pdf) 27. februar 2008. Henta 1. september 2011.
- ↑ William Garnett (1850-1932) - Brief biography on the British Society for the History of Mathematics
- ↑ Ashford, Oliver M. (1985). Prophet or Professor?: Life and Work of Lewis Fry Richardson. Bristol: Adam Hilger. ISBN 978-0852747742.
- ↑ «Royal Society election citation EC/1926/21». The Royal Society. 1926. Henta 1. september 2011.
- ↑ Körner, T. W. (1996). The Pleasures of Counting. Cambridge: Cambridge University Press. ISBN 978-0521568234. 544pp "A Quaker mathematician" (Ch 8) and "Richardson on war" (Ch 9)
- ↑ Lewis F. Richardson (1961). «The problem of contiguity: An appendix to Statistics of Deadly Quarrels». General Systems: Yearbook of the Society for the Advancement of General Systems Theory. (Ann Arbor, Mich.: The Society, [1956–: Society for General Systems Research) 6 (139): 139–187. ISSN 0072-0798. OCLC 1429672. «In the previous section integrals were taken around simple geometrical figures, as a preliminary to taking them around frontiers shown on political maps. An embarrassing doubt arose as to whether actual frontiers were so intricate as to invalidate that otherwise promising theory. A special investigation was made to settle this question. Some strange features came to notice; nevertheless an over-all general correction was found possible. The results will now be reported. ... As an explanation of how chance can arise in a world which he regarded as strictly deterministic, Heri Poincare* (no date) drew attention to insignificant causes which produced very noticeable effects. Sea coasts provide an apt illustration.»
- ↑ Fractals and the Fractal Dimension (Vanderbilt University website, vitja 30. januar 2008)
- ↑ «The Richardson Effect». www.futilitycloset.com. 2. desember 2013.
- ↑ Michael A. Ainslie Principles of Sonar Performance Modelling, Springer, 2010 ISBN 3-540-87661-8, s. 10
- Denne artikkelen bygger på «Lewis Fry Richardson» frå Wikipedia på bokmål, den 31. august 2011.
- Lynch, Peter: «Richardson's forecast: What went wrong?», juni 2004, National Oceanic and Atmospheric Administration (NOAA)
- Lynch, Peter: «The Emergence of Numerical Weather Prediction: Richardson's Dream», 2006, Cambridge University Press, ISBN 978-0521857291
- O'Connor, John J.; Robertson, Edmund F., «Lewis Fry Richardson», MacTutor History of Mathematics archive