Read other articles:

In mathematics, Fenchel's duality theorem is a result in the theory of convex functions named after Werner Fenchel. Let ƒ be a proper convex function on Rn and let g be a proper concave function on Rn. Then, if regularity conditions are satisfied, inf x ( f ( x ) − g ( x ) ) = sup p ( g ∗ ( p ) − f ∗ ( p ) ) . {\displaystyle \inf _{x}(f(x)-g(x))=\sup _{p}(g_{*}(p)-f^{*}(p)).} where ƒ * is the convex conjugate of ƒ (also referred to as the Fenche...

Bagian dari seri tentang:Islamisme Dasar Islam Sejarah Budaya Ekonomi Politik Sekularisme Ideologi Islamisme Qutbisme Salafisme Islamisme Syiah Fundamentalisme Islam Konsep Kekhalifahan Demokrasi Islam Sosialisme Islam Negara Islam Monarki Islam Republik Islam Islamisasi (pengetahuan) Jihad Pan-Islamisme Pasca-Islamisme Syariah Syura Perbudakan Teori dua bangsa Umat Pengaruh Anti-imperialisme Anti-Zionisme Kebangkitan Islam Zaman Kejayaan Islam GerakanMazhab Ahl-i Hadith Deobandi Madkhal...

البيت بيتك البلد مصر  لغة العمل العربية  IMDb.com صفحة البرنامج  تعديل مصدري - تعديل   شعار البرنامج البيت بيتك برنامج مصري منوع كان يذاع خمس مرات أسبوعياً على القناة الثانية المصرية والفضائية المصرية بالتلفزيون المصري، رئيس تحرير البرنامج الكاتب الصحفى محمد هانى م�...

  كاستيلو دي غراسيمونيوزا (بالإسبانية: Castillo de Garcimuñoz)‏[1]   - بلدية -    كاستيلو دي غراسيمونيوزا كاستيلو دي غراسيمونيوزا تقسيم إداري البلد إسبانيا[2]  [3] المقاطعة قونكة خصائص جغرافية إحداثيات 39°39′37″N 2°22′48″W / 39.660277777778°N 2.38°W / 39.66027...

Wali Kota TegalPetahanaDadang Somantrisejak 23 Maret 2019KediamanJalan Ki Gede Sebayu 1 Kota TegalMasa jabatan5 tahunPejabat pertamaD.J. SpanjaardSitus webSitus Resmi Kota Tegal Artikel ini memuat daftar wali kota Tegal, dari masa ke masa. No Wali Kota Mulai menjabat Akhir menjabat Prd. Ket. Wakil Wali Kota 1 Dirk Johannes Spanjaard 1929 1933 1 2 J.J.Ph. Koppenol 1933 1935 2 3 A.M. Pino 1935 1937 3 4 Mr. W.A. Court 1937 1941 4 5 H. Leenmans 1941 1942 5 6 Mr. Besar Mertokoesoemo 1942 1945...

Untuk kegunaan lain, lihat Gambir (disambiguasi). Gambir Uncaria rhynchophylla Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Plantae (tanpa takson): Trachaeophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Superasterids (tanpa takson): Asterids Ordo: Gentianales Famili: Rubiaceae Subfamili: Cinchonoideae Tribus: Naucleeae Genus: UncariaSchreber Spesies tipe Uncaria guianensis(Aublet) J.F. Gmelin Spesies Lihat teks Gambir (genus Uncaria) adalah genus tumbuhan yang ...

1975 film by François Truffaut The Story of Adèle H.Theatrical release posterDirected byFrançois TruffautScreenplay by François Truffaut Jean Gruault Suzanne Schiffman Frances Vernor Guille (collaboration) Jan Dawson (English adaptation) Based onLe Journal d'Adèle Hugoby Adèle HugoProduced byMarcel Berbert[citation needed]Starring Isabelle Adjani Bruce Robinson Sylvia Marriott Joseph Blatchley Ivry Gitlis CinematographyNestor AlmendrosEdited by Yann Dedet Martine Barraqué Jean ...

William E. Simon Bill Simon adalah seorang politikus Amerika, lahir tahun 1951 di Amerika Serikat, partisan, aktif di Partai Republik, yang nasional aktif dan efektif. Lihat WATCH TV LIV Simon's attack on Davis backfires Referensi Wikimedia Commons memiliki media mengenai William E. Simon. lbs Menteri Luar Negeri Amerika SerikatMenteri Urusan Luar Negeri1781–1789 R. Livingston Jay Menteri Luar Negeri1789–sekarang Jefferson Randolph Pickering J. Marshall Madison Smith Monroe Adams ...

Cet article est une ébauche concernant un acteur américain. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les conventions filmographiques. Lou WagnerBiographieNaissance 14 août 1948 (75 ans)San JoséNationalité américaineActivités Acteurmodifier - modifier le code - modifier Wikidata Lou Wagner est un acteur américain né le 14 août 1948 à San José, en Californie (États-Unis). Biographie Cette section est vide, insuffisamment détaillée ou ...

Министерство природных ресурсов и экологии Российской Федерациисокращённо: Минприроды России Общая информация Страна  Россия Юрисдикция Россия Дата создания 12 мая 2008 Предшественники Министерство природных ресурсов Российской Федерации (1996—1998)Министерство охраны...

Upper house of the German Empire's parliament This article is about the Bundesrat of the German Empire (1871–1918). For the current legislative body, see German Bundesrat. Bundesrat Deutscher BundesratLegislative body of GermanyTypeTypeUpper house HistoryEstablished1871Disbanded1918Preceded byBundesrat of the North German ConfederationSucceeded byReichsrat of the Weimar RepublicSeats61 (at dissolution)ElectionsVoting systemAppointedMeeting placeLeipziger Straße 4, Berlin (1871–...

Professional diving team leader responsible for safety A dive team listens to a safety brief from their dive supervisor For recreational diving supervision, see Divemaster and Dive leader. Not to be confused with Dive Supervisor. The diving supervisor is the professional diving team member who is directly responsible for the diving operation's safety and the management of any incidents or accidents that may occur during the operation; the supervisor is required to be available at the control...

  لمعانٍ أخرى، طالع أذربيجان (توضيح).أذربيجانمعلومات عامةالبلد إيران الإحداثيات 37°36′N 47°00′E / 37.6°N 47°E / 37.6; 47 التقسيمات الإدارية محافظة أذربيجان الشرقيةمحافظة أذربيجان الغربيةمحافظة أردبيل أتروباتين تعديل - تعديل مصدري - تعديل ويكي بيانات الأقاليم الثلا�...

American political activist, editor, and rabbi (born 1943) Michael LernerLerner at Occupy Oakland, November 2011Born1943 (age 80–81)Newark, New Jersey, USAlma materUniversity of California, BerkeleyWright InstituteOccupationsRabbieditorEmployersBeyt Tikkun SynagogueTikkunSpousesNan Fink (div. 1991) Deborah Kohn-Lerner ​ ​(m. 1998; div. 2014)​ Cat Zavis ​(m. 2015)​ChildrenAkiva Jeremiah Lerner Mic...

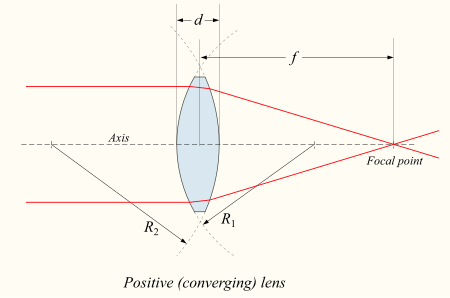
Lensa dapat dianggap sebagai lensa tipis jika ketebalannya jauh lebih kecil daripada jari-jari kelengkungan permukaannya (d ≪ |R1| dan d ≪ |R 2|). Dalam optik, 'lensa tipis adalah lensa dengan ketebalan (jarak sepanjang sumbu optik antara dua permukaan lensa) yang dapat diabaikan dibandingkan dengan jari-jari kelengkungan permukaan lensa. Lensa yang ketebalannya tidak dapat diabaikan terkadang disebut lensa tebal. approksimasi lensa tipis mengabaikan efek optik karena ...

AlmopiaΑλμωπία Letak Zona waktu: EET/EEST (UTC+2/3) Pemerintah Negara: Yunani Periferal: Makedonia Tengah Wali kota: Dimitris Pasois Statistik penduduk (pada 2011[1]) Kotamadya  - Jumlah penduduk: 27.556  - Luas: 985,8 km² (381 sq mi)  - Kepadatan: 28 /km² (72 /sq mi) Kode Almopia (bahasa Yunani: Αλμωπία), atau Enotia, juga dikenal pada Abad Pertengahan dengan sebutan Moglena (Yunani: Μογλενά, Make...

Hubungan Tiongkok-Rusia beralih ke halaman ini. Untuk Hubungan negara Tiongkok-Rusia sebelum 1991, lihat Sejarah Tiongkok-Rusia. Hubungan Tiongkok-Rusia Rusia Tiongkok Dmitry Medvedev dengan Hu Jintao saat kunjungan negara di Beijing pada Mei 2008. Anggota SCO dan CSTO Hubungan diplomatik antara Tiongkok dan Rusia secara dramatis terjadi setelah pembubaran Uni Soviet dan pendirian Federasi Rusia pada 1991. Kedua negara tersebut berbagi perbatasan tanah yang panjang yang yang diatur pada 1991,...

British colonial administrator (1844–1908) Sir Arthur HavelockGCSI GCMG GCIEPresident of NevisIn office6 April 1877 – 1878Preceded byRoger GoldsworthySucceeded byCharles Spencer SalmonGovernor of Sierra LeoneIn office27 June 1881 – September 1884MonarchQueen VictoriaPreceded bySir Samuel RoweSucceeded bySir Samuel Rowe35th Governor of TrinidadIn office24 January 1885 – 1885Preceded bySir Sanford FreelingSucceeded byWilliam RobinsonGovernor of Nat...

La pendenza è il grado di ripidità o di inclinazione di una strada o di un tratto di percorso. La pendenza di una strada è indicata dalla segnaletica verticale con cartelli di pericolo che indicano la pendenza con una percentuale. Il termine pendenza è un termine usato anche in geometria analitica. Indice 1 Pendenza puntuale 1.1 Non linearità della pendenza 2 Pendenza media 3 Valori notevoli 3.1 Pendenze massime ammissibili stradali 3.2 Pendenze massime ferroviarie 3.3 Pendenza massima p...

Cá hồng két Cá hồng két hay còn gọi là cá Két đỏ, cá huyết anh vũ, còn được biết đến với tên gọi tiếng Anh là blood parrot cichlid, parrot cichlid, bloody parrot là một loài cá lai được hình thành do kết quả lai tạo trong họ Cichlidae. Chúng được lai tạo ở Đài Loan vào những năm 1986. Hiện phổ biến hai giả thuyết tổ hợp lai của cá hồng két: Amphilophus labiatus X Heros severus Amphilophus citrinellum ...