Read other articles:

French Interior Minister since 2020 Gérald DarmaninDarmanin in 2019Minister of the Interior and OverseasIncumbentAssumed office 6 July 2020Prime MinisterJean CastexÉlisabeth BorneGabriel AttalPreceded byChristophe CastanerMinister of Public Action and AccountsIn office17 May 2017 – 6 July 2020Prime MinisterÉdouard PhilippePreceded byChristian Eckert (Secretary of State for the Budget and Public Accounts)Succeeded byOlivier DussoptMayor of TourcoingIn office23 May 2020 �...

Voce principale: Promozione 1986-1987. Promozione Lombarda 1986-1987 Competizione Promozione Sport Calcio Edizione 31ª Organizzatore FIGC - LNDComitato Regionale Lombardo Luogo  Italia Partecipanti 64 Formula 4 gironi all'italiana Cronologia della competizione 1985-1986 1987-1988 Manuale Nella stagione 1986-1987 la Promozione era il sesto livello del calcio italiano (il massimo livello regionale). Qui vi sono le statistiche relative al campionato in Lombardia e nella provincia di Piace...

Peta wilayah Mewar. Mewar atau Mewāḍ (Hindi: मेवाड़) adalah sebuah wilayah yang terletak di Rajasthan selatan-tengah di India barat. Wilayah ini mencakup Distrik Bhilwara, Chittorgarh, Rajsamand, Udaipur, dan Pratapgarh. Mewar berbatasan dengan Pegunungan Aravali di barat laut, Ajmer di utara, Gujarat dan Vagad di selatan, Malwa di tenggara, dan Hadoti di timur. Wilayah ini pernah dikuasai oleh Kerajaan Mewar (atau Udaipur) selama berabad-abad; kerajaan ini kemudian menjadi wil...

Chemical compound ToxiferineIdentifiersCAS Number302-30-7PubChem CID5281411ChemSpider4444760UNII9M7D9K3OJIChEMBLChEMBL231047CompTox Dashboard (EPA)DTXSID30897243 Chemical and physical dataFormulaC40H46N4O2Molar mass614.834 g·mol−13D model (JSmol)Interactive image SMILES [H][C@@]12[C@@]3(CC[N+]2(C)C/C4=C/CO)[C@@]5([H])N(C6=C3C=CC=C6)/C=C7[C@]([C@@]8(CC[N+]9(C)C/%10)[C@]9([H])C[C@]\7([H])C%10=C/CO)([H])N(C%11=C8C=CC=C%11)/C=C5/[C@]4([H])C1 Toxiferine (C-toxiferine I) is a curare toxin. ...

Neighborhood in Hillsborough County, Florida, US Ybor redirects here. For the cigar manufacturer after whom Ybor City is named, see Vicente Martinez Ybor. Neighborhood in Hillsborough County, Florida, United StatesYbor CityNeighborhoodCentro Ybor complex with a TECO Line car passing in front FlagNickname: Florida's Latin QuarterYbor CityCoordinates: 27°57′41″N 82°26′42″W / 27.96139°N 82.44500°W / 27.96139; -82.44500CountryUnited StatesStateFloridaCount...

Traveling by boat for pleasure This article is about yacht cruising. For cruising on cruise liners, see Cruise ship. A cruising sailboat anchored in the San Blas Islands, in Panama. Cruising is a maritime activity that involves staying aboard a watercraft for extended periods of time when the vessel is traveling on water at a steady speed. Cruising generally refers to leisurely trips on yachts and luxury cruiseships, with durations varying from day-trips to months-long round-the-world voyages...

Nazi Germany textile company Többens and SchultzTextile manufacturing plant in the Warsaw GhettoNative nameTöbbens und Schultz & CoCompany typeSlave labourIndustryTextile manufacturingOwnersFritz Schultz, Walter TöbbensNumber of employees18,000 (1942) Többens and Schultz (German: Többens und Schultz & Co) was a Nazi German textile manufacturing conglomerate making German uniforms, socks and garments in the Warsaw Ghetto and elsewhere,[1] during the occupation of Pola...

  关于与「友谊勋章 (俄罗斯)」標題相近或相同的条目页，請見「友谊勋章 (消歧义)」。 友谊勋章类型单级勋章（仅设有一个等级）授予原因加强各民族友谊、交流与合作国家／地区俄罗斯 颁发单位 俄羅斯颁授资格俄罗斯国民及世界各民族人民設立時間1994年3月2日[1]首次颁发康斯坦丁·蒂托夫（萨马拉州州长）绶带 优先顺序上等荣誉勋章下等光荣父母�...

Державний комітет телебачення і радіомовлення України (Держкомтелерадіо) Приміщення комітетуЗагальна інформаціяКраїна  УкраїнаДата створення 2003Керівне відомство Кабінет Міністрів УкраїниРічний бюджет 1 964 898 500 ₴[1]Голова Олег НаливайкоПідвідомчі ор...

Howard Cosell Información personalNombre de nacimiento Howard William Cohen Nombre en inglés Howard William Cosell Nacimiento 25 de marzo de 1918 Winston-Salem (Estados Unidos) Fallecimiento 23 de abril de 1995 (77 años)Manhattan (Estados Unidos) Causa de muerte Insuficiencia cardíaca Sepultura Westhampton Cemetery Nacionalidad EstadounidenseFamiliaHijos 2 EducaciónEducado en Escuela de Derecho de la Universidad de Nueva YorkUniversidad de Nueva YorkAlexander Hamilton High SchoolBoys Hig...

Військово-музичне управління Збройних сил України Тип військове формуванняЗасновано 1992Країна  Україна Емблема управління Військово-музичне управління Збройних сил України — структурний підрозділ Генерального штабу Збройних сил України призначений для планува...

Monarchist movement in Serbia Part of the Politics seriesMonarchy Central concepts MonarchMonarchismDivine right of kingsMandate of HeavenRoyal prerogative Types Abdication system Absolute Chinese Legalist Composite Constitutional Crowned republic Diarchy Dual Duchy Grand Dynastic union Elective Emirate Ethnarch Federal Hereditary Khanate Non-sovereign Pentarchy Personal union Popular Principality Real union Regency Coregency Self-proclaimed Signoria Tetrarch Triarchy Universal Philosophy Phi...

2015 EP by Dej Loaf...And See That's the ThingEP by Dej LoafReleasedJuly 31, 2015Recorded2015GenreHip hopLength23:01LabelColumbiaProducer DDS Go Grizzly iRocksays Izze The Producer The-A-Team Smash David J. Vaughn Dej Loaf chronology Sell Sole(2014) ...And See That's the Thing(2015) Singles from ...And See That's the Thing Back UpReleased: July 15, 2015[1] Hey ThereReleased: July 23, 2015[2] ...And See That's the Thing (stylized as #AndSeeThatsTheThing) is the first ex...

Eggs of the pollock fish Alaska pollock roeAlaska pollack's liver (top, center), roe (left), and milt (bottom)Korean nameHangul명란Hanja明卵Literal meaningAlaska pollock roeTranscriptionsRevised RomanizationmyeongnanMcCune–ReischauermyŏngnanJapanese nameKanji鱈子KanaたらこTranscriptionsRevised HepburntarakoRussian nameRussianикра минтаяRomanizationikra mintaya Pollock roe, also pollack roe (also known as myeongnan and tarako) is the roe of Alaska pollock (Gadus chalcogra...

This list of earthquakes in Bulgaria is organized by date and includes events that caused injuries/fatalities, historic quakes, as well events that are notable for other reasons. Seismic hazard map of Bulgaria, showing the calculated Peak Ground Acceleration in terms of g for a 475 year period Earthquakes Key   Epicenter outside Bulgaria Name Date Epicentre Mag. MMI Depth (km) Notes Deaths Injuries 1802 Vrancea earthquake 1802101400001802-10-14 Vrancea Mountains, Romania 7.9 VIII 150.0 ...

Fictional characters by Dashiell Hammett Fictional character Nick and Nora Charles(William Powell and Myrna Loy as Nick & Nora in the 1939 film Another Thin Man).First appearanceThe Thin ManCreated byDashiell HammettPortrayed byWilliam Powell & Myrna Loy (film, 1934–1947) Les Damon/Les Tremayne/David Gothard/Joseph Curtin & Claudia Morgan (radio, 1941–1950) Peter Lawford & Phyllis Kirk (TV, 1957–1959) Craig Stevens & Jo Ann Pflug (TV film) Barry Bostwick & Joanna...

Right of people to travel within and outside of their own country This article is about the right to travel. For the mechanical concept, see Range of motion. Free movement of persons redirects here. For the freedom of movement within the European Union, see Freedom of movement for workers in the European Union and European Single Market. Freedom of movement, mobility rights, or the right to travel is a human rights concept encompassing the right of individuals to travel from place to place wi...

Dynasty in northwest China (1038–1227) For other dynasties with the same name, see Xia (disambiguation). Xi Xia and Xixia redirect here. For the Chinese general whose name may be transliterated as Xi Xia, see Xi Qia. For locations, see Xixia (disambiguation). Great Xia大夏 (白高大夏國) (大白高國)1038–1227Location of Western Xia in 1111 (green in north west)Western Xia in 1150CapitalXingqing (modern Yinchuan)Common languagesTangutChineseReligion BuddhismTaoismConfucianismCh...

Former British imperial territories Not to be confused with United States of America. For the British Empire's colonial territories in the Americas before 1783, see British America. British North America1783–1907 Flag of the United Kingdom (1801 onward)Anthem: God Save The King/QueenStatus Colonies of Great Britain (1783–1800) Colonies of the United Kingdom of Great Britain and Ireland (1801–1907) CapitalAdministered from London, EnglandCommon languagesEnglish, French, GaelicR...

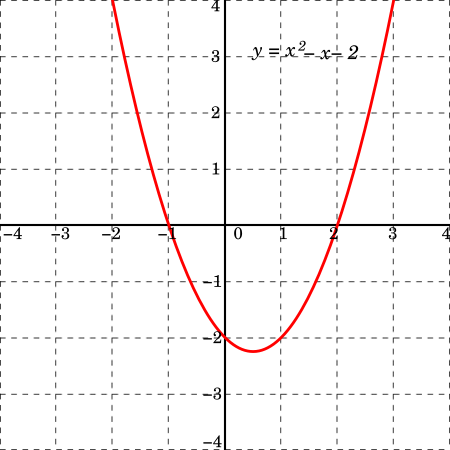
Polynomial function of degree two For the zeros of a quadratic function, see Quadratic equation and Quadratic formula. In mathematics, a quadratic polynomial is a polynomial of degree two in one or more variables. A quadratic function is the polynomial function defined by a quadratic polynomial. Before the 20th century, the distinction was unclear between a polynomial and its associated polynomial function; so quadratic polynomial and quadratic function were almost synonymous. This is still t...