Read other articles:

Halaman ini berisi artikel tentang sebuah spesies tumbuhan berbunga yang disebut Medlar Jepang. Untuk penggunaan lain, lihat Medlar. Untuk band, lihat Loquat (band). BiwaEriobotrya japonica Dedaunan dan buah-buahan Loquat Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Rosids Ordo: Rosales Famili: Rosaceae Genus: Eriobotrya Spesies: E. japonica Nama binomial Eriobotrya japonica(Thunb.) Lindl. Sinonim[1] Crataegus bibas L...

Kaseifu no MitaPoster Kaseifu no MitaGenreDrama keluargaDitulis olehKazuhiko YukawaSutradaraRyuichi Inomata, Toya Sato, Jun Ishio, Ken HigurashiPemeran Nanako Matsushima Yumi Shirakawa Hiroki Hasegawa Shiori Kutsuna Taishi Nakagawa Shūto Ayabe Miyu Honda Saki Aibu Penggubah lagu temaYoshihiro Ike,Kazuyoshi SaitoLagu pembukaMain Thema of MitaLagu penutupYasashiku NaritaiPenata musikYoshihiro IkeNegara asal JepangBahasa asliJepangJmlh. musim1Jmlh. episode11ProduksiProduser eksekuti...

Artikel ini bukan mengenai Roronoa Zoro. Zoroaster𐬰𐬀𐬭𐬀𐬚𐬎𐬱𐬙𐬭𐬀ZaraθuštraPersepsi Zoroastrian India mengenai sosok Zoroaster, diadaptasi dari sebuah patung yang dipahat pada abad ke-4 yang ditemukan di Taq-e Bostan, Iran Barat Daya. Yang asli sekarang diyakini sebagai representasi dari Mithra atau Hvare-khshaeta.[1]Dihormati diZoroastrianismeMenikhenismeBaha'iMithraismeAhmadiyah Zoroaster,[note 1] juga dikenal sebagai Zarathustra,[note 2] ...

Megavirus Megavirus chilensis TaksonomiSuperdomainBiotaDomainVirusFamiliMimiviridaeFamiliMegamimivirinaeGenusMegavirusSpesiesMegavirus chilensis lbs Megavirus[1] adalah genus virus yang hanya memiliki spesies tunggal yang diidentifikasi bernama Megavirus chilensis, yang secara filogenetik terkait dengan Acanthamoeba polyphaga Mimivirus (APMV).[2] Dalam penyebutan umum, Megavirus chilensis lebih sering disebut sebagai Megavirus. Hingga ditemukannya Pandoravirus pada tahun 2013,...

جمهورية مصر العربيةوزارة الدولة للإنتاج الحربي وزارة الدولة للإنتاج الحربي (مصر)الشعار البلد  مصر المقر الرئيسي العاصمة الإدارية، محافظة القاهرة تاريخ التأسيس 1966 (منذ 58 سنة) النوع وزارة العضوية مجلس الوزراء المصري اللغات الرسمية العربية الوزير محمد صلاح مصطفى[1] ا�...

Magic Hour the Series 2Genre Drama Roman BerdasarkanMagic HourSkenario Sukhdev Singh Tisa T.S. SutradaraAsep KusdinarPemeran Dimas Anggara Michelle Ziudith Maxime Bouttier Nadya Arina Yunita Siregar Dimaz Andrean Negara asalIndonesiaBahasa asliBahasa IndonesiaJmlh. musim2Jmlh. episode6ProduksiProduser Sukhdev Singh Wicky V. Olindo Pengaturan kameraMulti-kameraDurasi38–44 menitRumah produksiScreenplay FilmsRilis asliJaringan iflix WeTV Rilis18 Januari (2019-01-18) –18 Januari 20...

American graduate fellowship This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Harry S. Truman Scholarship – news · newspapers · books · scholar · JSTOR (September 2023) (Learn how and when to remove this template message) AwardHarry S. Truman ScholarshipAwarded forGraduate study in the United States for public service leadershipSponsored byHarry S. Truma...

Anastasia MyskinaKebangsaan RusiaTempat tinggalMoskwa, RusiaTinggi1.74 m (5 ft 8½ in)Berat59 kg (130½ lb)Memulai pro1998Tipe pemainKanan; backhand dengan dua tanganTotal hadiahUS$ 5,520,478TunggalRekor (M–K)252-141Gelar10Peringkat tertinggiNo. 2 (13 September, 2004)Hasil terbaik di Grand Slam (tunggal)Australia TerbukaQF (2003, 2004)Prancis TerbukaW (2004)WimbledonQF (2005, 2006)AS TerbukaQF (2003)GandaRekor (M–K)72-71Gelar5Peringkat tertinggiNo. 15 (21 Februari, 2005)Statisti...

Election in Rhode Island Main article: 1844 United States presidential election 1844 United States presidential election in Rhode Island ← 1840 November 1 - December 4, 1844 1848 →   Nominee Henry Clay James K. Polk Party Whig Democratic Home state Kentucky Tennessee Running mate Theodore Frelinghuysen George M. Dallas Electoral vote 4 0 Popular vote 7,322 4,867 Percentage 59.55% 39.58% President before election John Tyler Independent Elected Pre...

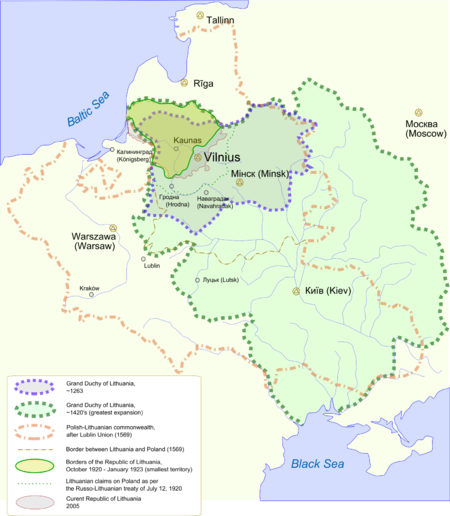
Disambiguazione – Se stai cercando altri significati, vedi Repubblica di Lituania. Lituania (dettagli) (dettagli) (LT) Tautos jėga vienybėje(IT) La forza del popolo è nell'unità! Lituania - LocalizzazioneLa Lituania (verde scuro) nell'Unione europea (verde chiaro) Dati amministrativiNome completoRepubblica di Lituania Nome ufficialeLietuvos Respublika Lingue ufficialiLituano Altre linguePolacco, Russo Capitale Vilnius  (580 020 ab. / 2020) PoliticaForma di gove...

الفريق ياسين باشا الهاشمي معلومات شخصية الميلاد سنة 1882 [1]  بغداد  الوفاة 21 يناير 1937 (54–55 سنة)[1]  دمشق  سبب الوفاة نوبة قلبية  مواطنة الدولة العثمانية العراق  مناصب رئيس وزراء العراق (4 )   في المنصب2 أغسطس 1924  – 26 يونيو 1925  جعفر العسكري  عب...

Multi-sport event in Innsbruck, Austria IX Olympic Winter GamesEmblem of the 1964 Winter Olympics[a]Host cityInnsbruck, AustriaNations36Athletes1,091 (892 men, 199 women)Events34 in 6 sports (10 disciplines)Opening29 January 1964Closing9 February 1964Opened byPresident Adolf SchärfCauldronJosl RiederStadiumBergiselWinter← Squaw Valley 1960Grenoble 1968 → Summer← Rome 1960Tokyo 1964 → Part of a series on 1964 Winter Olympics Bid process (bid...

Speech presented by a single character For the Soviet film, see Monologue (film). For the Malayalam film, see Anantaram. For the speech of a narrator, see Voiceover. Actor Christopher Walken performing a monologue in the 1984 stage play Hurlyburly In theatre, a monologue (from Greek: μονόλογος, from μόνος mónos, alone, solitary and λόγος lógos, speech) is a speech presented by a single character, most often to express their thoughts aloud, though sometimes also to directl...

Department of the Republic of the Congo Department in Republic of the CongoNiari NiadiDepartmentNiari, department of the Republic of the CongoCountryRepublic of the CongoCapitalDolisieArea • Total25,942 km2 (10,016 sq mi)Population (2023 census) • Total334,863 • Density13/km2 (33/sq mi)HDI (2018)0.567[1]medium · 4th of 12 Niari (can also be written as Niadi[2]) is a department of the Republic of the Congo in the wes...

1940 Indian filmEk Hi BhoolDirected byVijay BhattProduced byVijay-Shankar BhattStarringP. JairajMehtabUmakantBaby MeenaMusic byShankar Rao VyasPandit Anuj (lyrics)ProductioncompanyPrakash PicturesRelease date 1940 (1940) Running time155 minutesCountryIndiaLanguageHindi Ek Hi Bhool (The Only Mistake) is a 1940 Hindi social drama directed by Vijay Bhatt.[1] The film was produced by Vijay and his brother Shankar Bhatt for Bhatt's production banner Prakash Pictures.[2] The M...

Politics of Samoa Constitution Executive O le Ao o le Malo (head of state) Tuimalealiʻifano Vaʻaletoʻa Sualauvi II Council of Deputies Prime Minister Fiamē Naomi Mataʻafa Deputy Prime Minister Tuala Iosefo Ponifasio Cabinet Ministries Legislative Legislative Assembly Speaker: Papali’i Li’o Taeu Masipau Members Judiciary Court of Appeal of Samoa Supreme Court Chief Justice: Satiu Simativa Perese Elections Recent elections General: 201120162021Next Political parties Administrative div...

Type of greenhouse gas emissions trading scheme Part of a series aboutEnvironmental economics Carbon price Carbon credit Carbon emission trading Carbon fee and dividend Carbon finance Carbon offset Carbon tax Emissions trading Environmental tax Personal carbon trading Pigovian tax Social cost of carbon Climate change Carbon footprint Climate change mitigation Food miles Concepts Bright green environmentalism Circular economy Climate finance Corporate sustainability Degrowth Disinvestment Eco-...

Tigre de Longdan Panthera zdanskyi Crâne holotype. 2.55–2.16 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Pléistocène inférieur.Classification Règne Animalia Embranchement Chordata Classe Mammalia Infra-classe Placentalia Ordre Carnivora Sous-ordre Feliformia Famille Felidae Sous-famille Pantherinae Genre Panthera Espèce† Panthera zdanskyiMazák (d), Christiansen (d) & Kitchener (d), 2011 Panthera zdanskyi, le Tigre de Longdan[1], est une espèce éteinte ...

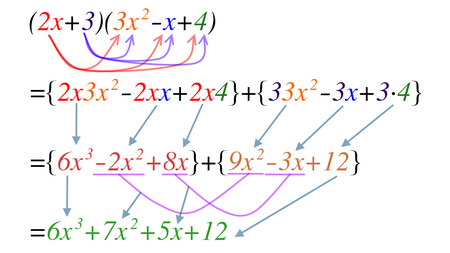
For locally approximating a function with a polynomial, see Taylor series. For graphs with sparse shallow minors, see Bounded expansion. In mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition. Expansion of a polynomial expression can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, contin...

You can help expand this article with text translated from the corresponding article in French. (December 2022) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikip...