NatŇęralusis skaińćius
|
Read other articles:
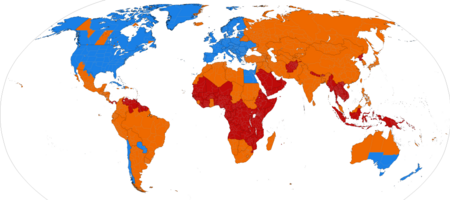
Untuk kegunaan lain, lihat DST. Walaupun tidak diterapkan oleh sebagian besar negara di dunia, waktu musim panas umum diterapkan di Dunia Barat. WMP diterapkan. WMP tidak lagi diterapkan. WMP tidak pernah diterapkan. Waktu Musim Panas (WMP) (Daylight Saving Time (DST) di Amerika Utara atau summer time di Inggris, Uni Eropa, dan tempat lainnya) adalah suatu praktik pemajuan jarum jam semasa musim panas sehingga malam hari datang pada pukul yang lebih lambat ...

Radio station in Windsor, Ontario, Canada For other stations that have used the CKLW callsign in the past, see CBET-DT and CIDR-FM. CKLWWindsor, OntarioBroadcast areaSouthwestern OntarioDetroit‚ÄďWindsorFrequency800 kHz (AM)BrandingAM 800 CKLWProgrammingFormatNews/TalkAffiliationsCHWI-DTThe Canadian PressPremiere NetworksWindsor SpitfiresOwnershipOwnerBell Media(Bell Media Radio)Sister stationsCHWI-DT, CIDR-FM, CIMX-FM, CKWWHistoryFirst air dateJune 2, 1932; 91 years ago (19...

Halaman ini berisi artikel tentang tokoh dalam Kitab Kejadian. Untuk nama yang merujuk pada tokoh ini, lihat Yusuf (nama). Untuk tokoh ini dalam sudut pandang Islam, lihat Yusuf dalam Islam. Untuk tokoh Perjanjian Baru, lihat Yusuf dari Nazaret dan Yusuf dari Arimatea. YusufNama dalam bahasa asli(he) ◊ô◊ē◊°◊£ BiografiKelahiran1915 SM ‚ÜĒ 1562 SM Haran (tempat dalam Alkitab) Kematian1805 SM ‚ÜĒ 1452 SM (109/110 tahun)Mesir Kuno Tempat pemakamanMakam Yusuf Gua Makhpela Nabi Yud...

Chilean television personality (born 1940) For other uses, see Don Francisco. In this Spanish name, the first or paternal surname is Kreutzberger and the second or maternal family name is Blumenfeld. Don FranciscoBornMario Luis Kreutzberger Blumenfeld (1940-12-28) 28 December 1940 (age 83)Talca, ChileNationalityChilean and AmericanCitizenshipChileOccupationTelevision hostYears active1962‚ÄďpresentTelevisionS√°bado GiganteDon Francisco PresentaDon Francisco te invitaSpouseTer...
Medical conditionHypertensive disease of pregnancyOther namesMaternal hypertensive disorderSpecialtyObstetricsFrequency20.7 million (2015)[1]Deaths46,900 (2015)[2] Hypertensive disease of pregnancy, also known as maternal hypertensive disorder, is a group of high blood pressure disorders that include preeclampsia, preeclampsia superimposed on chronic hypertension, gestational hypertension, and chronic hypertension.[3] Maternal hypertensive disorders occurred in about 2...

Borough in Estonia Small borough in L√§√§ne-Viru County, EstoniaSimunaSmall boroughAvanduse manor in Simuna.SimunaLocation in EstoniaCoordinates: 59¬į02‚Ä≤52‚Ä≥N 26¬į24‚Ä≤09‚Ä≥E / 59.04778¬įN 26.40250¬įE / 59.04778; 26.40250Country EstoniaCounty L√§√§ne-Viru CountyMunicipality V√§ike-Maarja ParishPopulation (01.08.2019[1]) ‚ÄĘ Total422 Simuna is a small borough in V√§ike-Maarja Parish, L√§√§ne-Viru County, in northeastern Estonia. It had a p...

Declaration of war in World War I Declaration of War with GermanyLong titleJoint Resolution Declaring that a State of War exists between the Imperial German Government and the Government and the people of the United States and making provision to prosecute the same.Enacted bythe 65th United States CongressEffectiveApril 6, 1917CitationsPublic lawPub. L.Tooltip Public Law (United States) 65‚Äď1Statutes at Large40 Stat. 1Legislative historyIntroduced in the Senate as S.J.Res...

French painter, draughtsman and etcher (d. 1682) Claude LorrainClaude Lorrain's self-portraitBornClaude Gell√©e1600 or 1604/5Chamagne, Duchy of LorraineDied21 November or 23 November 1682 (aged 77/78 or 82)Rome, Papal StatesKnown forPaintingMovementBaroqueSignature Claude Lorrain (French: [klod l…Ē. Ā…õŐÉ]; born Claude Gell√©e [ í…ôle], called le Lorrain in French; traditionally just Claude in English; c. 1600 ‚Äď 23 November 1682) was a French painter, draughts...

Kurau UtaraDesaKantor Desa Kurau Utara, Tanah LautPeta lokasi Desa Kurau UtaraNegara IndonesiaProvinsiKalimantan SelatanKabupatenTanah LautKecamatanBumi MakmurKode Kemendagri63.01.11.2002 Luas... km²Jumlah penduduk... jiwaKepadatan... jiwa/km² Kurau Utara adalah salah satu desa di Kecamatan Bumi Makmur, Tanah Laut, Kalimantan Selatan, Indonesia. Pranala luar (Indonesia) Keputusan Menteri Dalam Negeri Nomor 050-145 Tahun 2022 tentang Pemberian dan Pemutakhiran Kode, Data Wilayah Adminis...

ś≠§śĚ°ÁõģŚļŹŤ®ÄÁꆍäāś≤°śúČŚÖÖŚąÜśÄĽÁĽďŚÖ®śĖáŚÜÖŚģĻŤ¶ĀÁāĻ„Äā (2019ŚĻī3śúą21śó•)ŤĮ∑ŤÄÉŤôϜȩŚÖÖŚļŹŤ®ÄԾƜłÖśôįś¶āŤŅįśĚ°ÁõģśČÄśúČťá杼ě„ÄāŤĮ∑Śú®śĚ°ÁõģÁöĄŤģ®Ťģļť°ĶŤģ®Ťģļś≠§ťóģťĘė„Äā ŚďąŤź®ŚÖčśĖĮŚĚ¶ÁłĹÁĶĪŚďąŤĖ©ŚÖčÁłĹÁĶĪśóóÁŹĺšĽĽ“ö–į—Ā—č–ľ-–Ė–ĺ–ľ–į—Ä—ā –ö–Ķ–ľ–Ķ–Ľ“Ī–Ľ—č –Ę–ĺ“õ–į–Ķ–≤Ść°ÁĎüŚßÜŤč•ť©¨ŚįĒÁČĻ¬∑śČėŚć°ŤÄ∂Ś§ęŤá™2019ŚĻī3śúą20śó•Śú®šĽĽšĽĽśúü7ŚĻīť¶ĖšĽĽŚä™ŚįĒŤčŹšłĻ¬∑Áļ≥śČéŚįĒŚ∑īŤÄ∂Ś§ęŤģĺÁęč1990ŚĻī4śúą24śó•ÔľąŚďąŤĖ©ŚÖčŤėáÁ∂≠ŚüÉÁ§ĺśúÉšłĽÁĺ©ŚÖĪŚíĆŚúčÁłĹÁĶĪÔľČ ŚďąŤź®ŚÖčśĖĮŚĚ¶ ŚďąŤź®ŚÖčśĖĮŚĚ¶śĒŅŚļú...

SD Negeri Cinere 1InformasiDidirikan01 Januari 1950JenisNegeriAkreditasiANomor Statistik Sekolah101026607036Nomor Pokok Sekolah Nasional20228676Kepala SekolahMursidi S.PdRentang kelasI, II, III, IV, V, VIKurikulumKurikulum 2013StatusSekolah Standar NasionalAlamatLokasiJalan Cinere Raya ‚ĄĖ18, Cinere, Kec. Cinere, Depok, Jawa Barat, IndonesiaTel./Faks.(021) 7530548Situs webSitus [email protected] SD Negeri Cinere 1 adalah sebuah sekolah dasar negeri yang terletak d...

County in Indiana, United StatesFor other uses, see Shelby County (disambiguation). County in IndianaShelby CountyCountyShelby County Courthouse in ShelbyvilleLocation within the U.S. state of IndianaIndiana's location within the U.S.Coordinates: 39¬į31‚Ä≤N 85¬į47‚Ä≤W / 39.52¬įN 85.79¬įW / 39.52; -85.79Country United StatesState IndianaFoundedDecember 31, 1821 (authorized)1822 (organized)Named forIsaac ShelbySeatShelbyvilleLargest cityShelbyvilleArea ‚ÄĘ...

Statue in Chicago, Illinois, U.S. Equestrian statue of Philip SheridanThe statue in 2023Coordinates41¬į56‚Ä≤25.7‚Ä≥N 87¬į38‚Ä≤21.3‚Ä≥W / 41.940472¬įN 87.639250¬įW / 41.940472; -87.639250 An equestrian statue of Philip Sheridan by Gutzon Borglum, sometimes called the General Philip Henry Sheridan Monument, is installed in Chicago, in the U.S. state of Illinois.[1][2] History The sculpture was installed in 1923.[3][4] It was vandalized in ...

1948 novel by Ruth Park The Harp in the South First UK edition (publ. Michael Joseph)AuthorRuth ParkLanguageEnglishGenreFictionPublisherAngus & Robertson, AustraliaPublication date1948Publication placeAustraliaMedia typePrintPages229 ppISBN0-14-010456-9Preceded by‚Äď Followed byPoor Man's Orange The Harp in the South is the debut novel by New Zealand-born Australian author Ruth Park. Published in 1948, it portrays the life of a Catholic Irish Australian family li...

For related races, see 1976 United States gubernatorial elections. 1976 Missouri gubernatorial election ← 1972 November 2, 1976 1980 → Nominee Joseph Teasdale Kit Bond Party Democratic Republican Popular vote 971,184 958,110 Percentage 50.2% 49.6% County resultsTeasdale: 50‚Äď60% 60‚Äď70%Bond: 50‚Äď60% 60‚Äď70% Governor before election Kit ...

Seventh major release of Windows NT Operating system Windows VistaVersion of the Windows NT operating systemScreenshot of Windows Vista Ultimate, showing its desktop, taskbar, Start menu, Windows Sidebar, Welcome Center, and glass effects of Windows AeroDeveloperMicrosoftSource modelClosed-sourceSource-available (through Shared Source Initiative)[1]Released tomanufacturingNovember 8, 2006; 17 years ago (2006-11-08)[2]GeneralavailabilityJanuary 30, 2007&#...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2013) (Learn how and when to remove this message) 512th Airlift WingC-17 Globemaster III of the 436th and 512th Airlift WingsActive1949‚Äď1951; 1952‚Äď1971; 1973‚ÄďpresentCountry United StatesBranch United States Air ForceRoleAirliftPart ofAir Force Reserve CommandGarrison/HQDover Air Forc...

Galaxy in the constellation Cassiopeia NGC 147Hubble Space Telescope image of NGC 147Observation data (J2000 epoch)ConstellationCassiopeiaRight ascension00h 33m 12.1s[1]Declination+48° 30′ 32″[1]Redshift-193 ¬Ī 3 km/s[1]Distance2.53 ¬Ī 0.11 Mly (780 ¬Ī 30 kpc)[2][3][4][a]Apparent magnitude (V)10.5[1]CharacteristicsTypedSph/dE5[1]Apparent size (V)13.2‚Ä≤ √ó 7.8‚Ä≤[1]Notable featuressate...

ō™ō¨ŔÖōĻ ōßŔĄō≠ŔÜōßōī - ŔāōĪŔäō© - ō™Ŕāō≥ŔäŔÖ ō•ōĮōßōĪŔä ōßŔĄō®ŔĄōĮ ōßŔĄŔäŔÖŔÜ ōßŔĄŔÖō≠ōßŔĀōłō© ŔÖō≠ōßŔĀōłō© ō≠ō∂ōĪŔÖŔąō™ ōßŔĄŔÖōĮŔäōĪŔäō© ŔÖōĮŔäōĪŔäō© ōßŔĄōĻō®ōĪ ōßŔĄōĻō≤ŔĄō© ōĻō≤ŔĄō© ōßŔĄōĻō®ōĪ ōßŔĄō≥ŔÉōßŔÜ ōßŔĄō™ōĻōĮōßōĮ ōßŔĄō≥ŔÉōßŔÜŔä 2004 ōßŔĄō≥ŔÉōßŔÜ 56 ‚ÄĘ ōßŔĄōįŔÉŔąōĪ 29 ‚ÄĘ ōßŔĄō•ŔÜōßōę 27 ‚ÄĘ ōĻōĮōĮ ōßŔĄō£ō≥ōĪ 5 ‚ÄĘ ōĻōĮōĮ ōßŔĄŔÖō≥ōßŔÉŔÜ 5 ŔÖōĻŔĄŔąŔÖōßō™ ō£ōģōĪŔČ ōßŔĄō™ŔąŔāŔäō™ ō™ŔąŔāŔäō™ ōßŔĄŔäŔÖŔÜ (+3 ōļōĪŔäŔÜŔäō™ōī) ō™ōĻōĮÔŅĹ...

DEKRA SEJenisSocietas EuropaeaDidirikan1925Kantor pusatStuttgart, JermanTokoh kunciStefan K√∂lbl (CEO)Roland GerdonClemens KlinkeIvo RauhJ√∂rg MannspergerPendapatan‚ā¨1.86 billion (2010)Karyawan44,000[1]Situs webwww.dekra.com DEKRA adalah perusahaan inspeksi kendaraan Eropa yang didirikan di Berlin, Jerman pada tahun 1925 sebagai Deutscher Kraftfahrzeug-√úberwachungs-Verein (Asosiasi Inspeksi Kendaraan Bermotor Jerman).[2] Dengan sekitar 36.000 karyawan dan pendapatan sekitar ...








