R대칭
|
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Harold I. Johnston – berita · surat kabar · buku · cendekiawan · JSTOR Harold I. JohnstonPenerima Medal of HonorLahir(1892-03-09)9 Maret 1892Kendell, KansasMeninggal28 Agustus 1949(1949-08-28) (umur ...

Jill Biden Ibu Negara Amerika SerikatPetahanaMulai menjabat 20 Januari 2021PresidenJoe BidenWakil PresidenKamala Harris PendahuluMelania TrumpPenggantiPetahanaIstri Wakil Presiden Amerika SerikatMasa jabatan20 Januari 2009 – 20 Januari 2017PresidenBarack ObamaWakil PresidenJoe Biden PendahuluLynne CheneyPenggantiKaren Pence Informasi pribadiLahirJill Tracy Jacobs3 Juni 1951 (umur 72) Hammonton, New Jersey, Amerika SerikatPartai politikDemokratSuami/istriBill Stevenson (197...

Japanese folding knife Higonokami knives A higonokami (肥後守) is a type of folding pocket knife originating in Miki, Hyōgo Prefecture, Japan in 1896. The knife has no locking system, but is a friction folder or penny knife,[1] using the friction of the swivel or the pressure of the user's thumb on its iconic lever or chikiri, to prevent the knife from folding during use. The handle of the Higonokami is made of a folded over sheet of metal. The handle is stamped with the name of t...

محمد عزة دروزة محمد عزة دروزة في شبابه الأمين العام لحزب الاستقلال في المنصب1932 – 1947 المدير العام للأوقاف في فلسطين في المنصب1930 – 1937 معلومات شخصية اسم الولادة محمد عزة بن عبد الهادي دَرْوَزَة الميلاد 21 يونيو 1888 نابلس الوفاة 26 يوليو 1984 (96 سنة) دمشق مواطنة فل...

Bunga Citra LestariBunga pada tahun 2016Lahir22 Maret 1983 (umur 41)Jakarta, IndonesiaNama lainBCLPekerjaanPenyanyiaktrismodelTahun aktif1997—sekarangSuami/istriAshraf Sinclair (m. 2008; meninggal 2020) Tiko Aryawardhana (m. 2023)[1]Anak1Keluarga Intan Ayu Purnama (sepupu) Ivan Permana (sepupu) Sjarif Usman (kakek) Karier musikGenrePopInstrumen Vokal Label Aquarius Musikindo (2004–20...

American baseball player Baseball player Kyle KellerKeller with the Hanshin TigersYomiuri Giants – No. 33PitcherBorn: (1993-04-28) April 28, 1993 (age 30)Metairie, Louisiana, U.S.Bats: RightThrows: RightProfessional debutMLB: August 4, 2019, for the Miami MarlinsNPB: March 25, 2022, for the Hanshin TigersMLB statistics (through 2021 season)Win–loss record1–1Earned run average5.83Strikeouts48NPB statistics (through 2023 season)Win–loss record4–2Earn...

Phil Foden Foden bermain untuk Manchester City pada 2017Informasi pribadiNama lengkap Philip Walter Foden[1]Tanggal lahir 28 Mei 2000 (umur 23)[2]Tempat lahir Stockport, InggrisTinggi 171 cm (5 ft 7 in)[3]Posisi bermain Gelandang,PenyerangInformasi klubKlub saat ini Manchester CityNomor 47Karier junior2009–2016 Manchester CityKarier senior*Tahun Tim Tampil (Gol)2016– Manchester City 159 (49)Tim nasional‡2015–2016 Inggris U-16 8 (2)2016–20...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada April 2024. Gereja Keluarga Kudus, RamallahArab: كنيسة العائلة المقدسةcode: ar is deprecated Gereja Keluarga Kudus, RamallahLokasiRamallahNegara PalestinaDenominasiGereja Katolik RomaArsitekturStatusParokiStatus fungsionalAktifAdministrasiKeu...

Keuskupan AlbanyDioecesis AlbanensisKatolik LokasiNegara Amerika SerikatWilayahAlbany, Columbia, Delaware, Fulton, selatan Herkimer, Greene, Montgomery, Otsego, Rensselaer, Saratoga, Schenectady, Schoharie, Warren, dan WashingtonProvinsi gerejawiNew YorkDekanat14StatistikLuas10.419 sq mi (26.990 km2)Populasi- Total- Katolik(per Desember 2012)1.392.464330,000 (23.7%)Paroki129 (dengan 2 apostolat)Sekolah28InformasiDenominasiKatolik RomaGereja sui iurisGer...
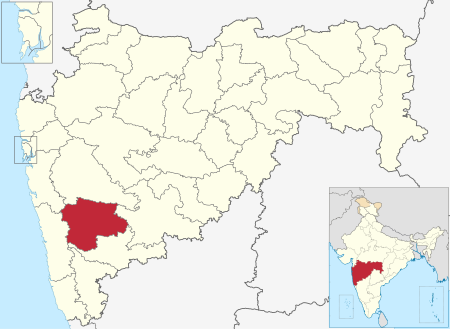
Hill fort in Maharashtra, India BhushangadSatara district, Maharashtra, India Bhushangad as seen from the plainsBhushangadShown within MaharashtraShow map of MaharashtraBhushangadBhushangad (India)Show map of IndiaCoordinates17°27′53″N 74°24′23″E / 17.4648°N 74.4063°E / 17.4648; 74.4063TypeHill Fort Bhushangad is a hill fort in the Khatav taluk of the Satara district of Maharashtra, India. It is oval in shape, and rises 600 feet (180 m) above the surro...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Railway station in Yao, Osaka Prefecture, Japan Yao Station八尾駅JR-West commuter rail stationYao Station, July 2014General informationLocation3-9 Yasunaka-chō, Yao-shi, Osaka-fu 581-0085JapanCoordinates34°37′3.2″N 135°35′48.3″E / 34.617556°N 135.596750°E / 34.617556; 135.596750Owned by JR WestOperated by JR WestLine(s) Q Kansai Main Line (Yamatoji Line)Distance163.1 km (101.3 mi) from Nagoya42.2 km (26.2 mi) from KamoPlat...

Pandemi koronavirus di AfghanistanJumlah kasus COVID-19 yang dikonfirmasi berdasarkan Provinsi di Afganistan pada 16 Mei 2020. 1–49 kasus terkonfirmasi 50–99 kasus terkonfirmasi 100–199 kasus terkonfirmasi 200–999 kasus terkonfirmasi ≥1000 kasus terkonfirmasiPenyakitCOVID-19Galur virusSARS-CoV-2LokasiAfghanistanKasus pertamaHeratTanggal kemunculan24 Februari 2020(4 tahun, 3 bulan, 1 minggu dan 1 hari)Asa...

Challenger Salinas 2010Sport Tennis Data11 gennaio – 16 gennaio Edizione15° SuperficieCemento CampioniSingolare Brian Dabul Doppio Jonathan Marray / Jamie Murray 2009 2011 Il Challenger Salinas 2010 è stato un torneo professionistico di tennis maschile giocato sul cemento, che faceva parte dell'ATP Challenger Tour 2010. Si è giocato a Salinas in Ecuador dall'11 al 16 gennaio 2010. Indice 1 Partecipanti 1.1 Teste di serie 1.2 Altri partecipanti 2 Campioni 2.1 Singolare 2.2 Doppio 3 Colleg...

← 2015 • • 2023 → Elecciones municipales en Cubas de la Sagra Fecha Domingo, 26 de mayo de 2019 Tipo municipales Lugar Cubas de la Sagra Cargos a elegir 25 concejales Resultados PP Votos 1,274 1.4 % Escaños obtenidos 6 7 45.02 % PSOE Votos 727 60.5 % Escaños obtenidos 3 1 25.69 % Ciudadanos Votos 553 Escaños obtenidos 3 12...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Southern Sydney – news · newspapers · books · scholar · JSTOR (February 2023) (Learn how and when to remove this message) Region in New South Wales, AustraliaSouthern SydneyNew South WalesSydney Airport, Botany Bay and surrounding suburbsLGA(s) Sydney Georges R...

6°19′26″S 134°54′53″E / 6.32389°S 134.91472°E / -6.32389; 134.91472 Pulau PenambulaiPulau PenambulaiPulau Penambulai (Indonesia)Pulau PenambulaiGeografiLokasiAsia TenggaraKoordinat6°22′31″S 134°51′25″E / 6.375278°S 134.856944°E / -6.375278; 134.856944KepulauanKepulauan MalukuPemerintahanNegaraIndonesiaProvinsiMalukuKabupatenKabupaten Kepulauan AruKependudukanPenduduk371 jiwa (2016)Info lainnyaZona waktuIEST (UTC+...
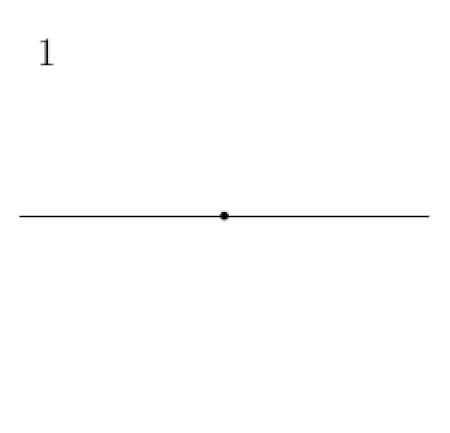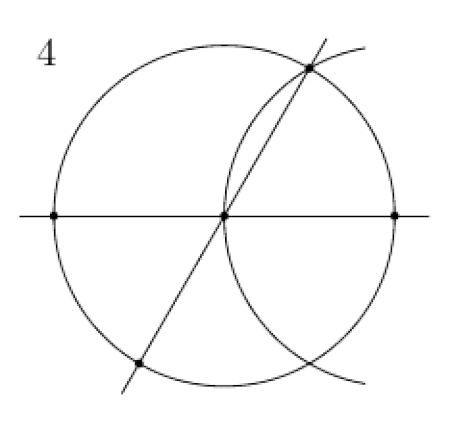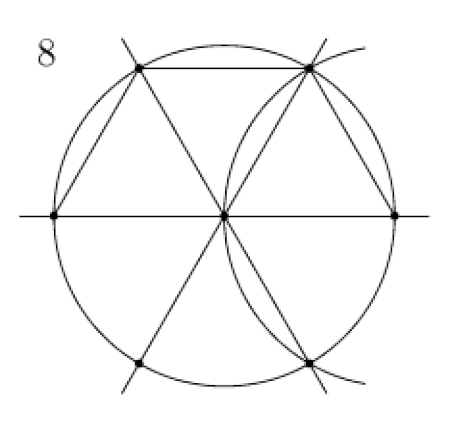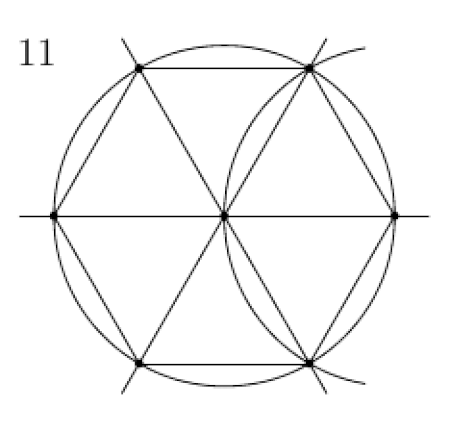
Hình họcHình chiếu một mặt cầu lên mặt phẳng. Đại cươngLịch sử Phân nhánh Euclid Phi Euclid Elliptic Cầu Hyperbol Hình học phi Archimedes Chiếu Afin Tổng hợp Giải tích Đại số Số học Diophantos Vi phân Riemann Symplectic Phức Hữu hạn Rời rạc Kỹ thuật số Lồi Tính toán Fractal Liên thuộc Khái niệmChiều Phép dựng hình bằng thước kẻ và compa Đỉnh Đường cong Đường chéo Góc Song song Vuông góc ...

Este artículo o sección tiene referencias, pero necesita más para complementar su verificabilidad. Busca fuentes: «DSports» – noticias · libros · académico · imágenesEste aviso fue puesto el 30 de noviembre de 2022. DSports Eslogan El canal del deporteTipo de canal Televisión por suscripciónProgramación DeportesPropietario Grupo WertheinOperado por Vrio TorneosFundación 13 de junio de 2009Inicio de transmisiones 13 de junio de 2009Formato de imagen 1080i HD...











































