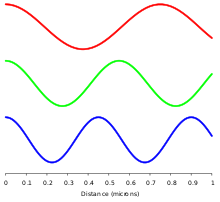
전자기파
|
Read other articles:

Blekutak Sepiella inermis Sepiella inermis (Van Hasselt, 1835)Status konservasiKekurangan dataIUCN162500 TaksonomiKerajaanAnimaliaFilumMolluscaKelasCephalopodaOrdoSepiidaFamiliSepiidaeGenusSepiellaSpesiesSepiella inermis Tata namaSinonim takson Diphtherosepion martini Rochebrune, 1884 Sepia affinis Souleyet, 1852 Sepia inermis Van Hasselt, 1835 Sepia microcheirus Gray, 1849 Sepia tourannensis Souleyet, 1852 Sepiella curta Pfeffer, 1884 Sepiella maindroni Rochebrune, 1884 lbs Sepiella inermis ...

On Such a NightSutradaraEwald André DupontProduserAdolph ZukorDitulis olehMorley F. CassidyS. S. FieldJohn D. KlorerPemeranGrant RichardsKaren MorleyRoscoe KarnsDistributorParamount PicturesTanggal rilis 27 Agustus 1937 (1937-08-27) Durasi71 menitNegaraAmerika SerikatBahasaInggris On Such a Night adalah sebuah film kejahatan Amerika Serikat tahun 1937 garapan Ewald André Dupont dan menampilkan Grant Richards, Karen Morley, dan Roscoe Karns. Film tersebut dibuat oleh Paramount Pictures ...

Duta Besar Yaman untuk IndonesiaPetahanaAbdulghani Nassr Ali Al-Shamirisejak 2018 Berikut adalah daftar duta besar Republik Yaman untuk Republik Indonesia. Nama Kredensial Selesai tugas Ref. Mohamed A. K Alwazir 2 Juli 1986 [1] Abdul Malik Mohamed Abdul Wasea Al Tayyeb 15 November 1989 [1] Mohammad Abdul Aziz Salam 15 Januari 1991 [1] Abdul Wahid Mohammed Faare 20 Juni 1995 [1] Abdulrahman Mohamed Alhothi 6 Februari 2006 [2] Ali Mohamed Alsoswa 21 ...

American judge Senator Trotter redirects here. For the Illinois State Senate member, see Donne Trotter. James Fisher TrotterUnited States Senatorfrom MississippiIn officeJanuary 22, 1838 – July 10, 1838Appointed byAlexander McNuttPreceded byJohn BlackSucceeded byThomas H. WilliamsMember of the Mississippi SenateIn office1829-1833Member of the Mississippi House of RepresentativesIn office1827-1829 Personal detailsBorn(1802-11-05)November 5, 1802Brunswick County, Virginia, USDied...

Negara Palestinaدولة فلسطين Daulat Filasṭin (Arab) Bendera Lambang Semboyan: فلسطين (Indonesia: Palestina)Lagu kebangsaan: فدائي Fida'i (Indonesia: Revolusiku) Lambang:Lambang ini digunakan untuk lambang PerangPerlihatkan BumiPerlihatkan peta BenderaStatusNegara yang diakui sebagian, negara pengamat PBBDiakui oleh 138 negara anggota PBBIbu kotaYerusalem(dipersengketakan)31°47′N 35°13′E / 31.783°N 35.217°E / 31.783; 35.217Pusat&...

Kowloon Generic Romance九龍ジェネリックロマンス(Kūron Jenerikku Romansu)GenreRoman[1] MangaPengarangJun MayuzukiPenerbitShueishaImprintYoung Jump ComicsMajalahWeekly Young JumpDemografiSeinenTerbit7 November, 2019 – sekarangVolume9 (Daftar volume) Portal anime dan manga Kowloon Generic Romance (Jepang: 九龍ジェネリックロマンスcode: ja is deprecated , Hepburn: Kūron Jenerikku Romansu) adalah seri manga Jepang yang ditulis dan diilustrasikan oleh Ju...

Questa voce sull'argomento calciatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Walter Negroni Nazionalità Italia Calcio Ruolo Difensore Carriera Squadre di club1 1926-1927 G.E.A. Firenze? (?)1928-1933 Parma108 (2)1933-1934 Salernitana22 (0)1934-1935 Siena5 (0)1935-1938 Parma67 (0)1938-1939 Pro Patria22 (1)1939-1940 Carbonia? (?)1940-1941 Perugia...

For other places with the same name, see Wronów (disambiguation). Village in Lublin Voivodeship, PolandWronówVillageWronówCoordinates: 51°10′N 22°9′E / 51.167°N 22.150°E / 51.167; 22.150Country PolandVoivodeshipLublinCountyLublinGminaBełżyce Wronów [ˈvrɔnuf] is a village in the administrative district of Gmina Bełżyce, within Lublin County, Lublin Voivodeship, in eastern Poland.[1] It lies approximately 9 kilometres (6 mi) west of Be...

This article may rely excessively on sources too closely associated with the subject, potentially preventing the article from being verifiable and neutral. Please help improve it by replacing them with more appropriate citations to reliable, independent, third-party sources. (June 2022) (Learn how and when to remove this message) Iowa Department of Health and Human ServicesAgency overviewFormed1937JurisdictionGovernment of IowaHeadquartersDes Moines, Iowa, U.S.Agency executiveKelly Kennedy Ga...

Imperial house order of Ethiopia Order of the Holy TrinitySet of the Imperial Order of the Holy Trinity.Awarded by EthiopiaTypeDynastic orderEstablished2 November 1930Royal houseSolomonic DynastyReligious affiliationEthiopian OrthodoxyRibbonRed with yellow edgesEligibilityEthiopian citizens and foreign nationals, both civilian and militaryAwarded forOutstanding service to the ThroneGradesGrand Cross with CollarGrand CrossPost-nominalsGCHT*GCHTFormer gradesGrand CrossGrand Offi...

Bombing of Reggio CalabriaPart of World War IIAerial photo taken during a British raid on Reggio Calabria in 1943Date1943LocationReggio Calabria, ItalyBelligerents United States United Kingdom Kingdom of Italy The bombing of Reggio Calabria was a series of attacks by the United States Army Air Force and the Royal Air Force on the Italian city of Reggio Calabria during World War II. All together, Reggio Calabria suffered 24 air raids, aimed at disabling its port facilities, ai...

Seventh major release of the classic Mac OS This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: System 7 – news · newspapers · books · scholar · JSTOR (Decembe...

British and Australian colony in Oceania from 1883 to 1975 Not to be confused with Territory of Papua and New Guinea. Territory of Papua1883–1975 Flag Badge Territory of Papua Queensland (annexed Papua in 1883) Other British possessionsStatusQueensland dependency (1883–1884)British protectorate (1884–1888)British colony (1888–1902)Australian external territory (1902–1975)CapitalPort MoresbyCommon languagesEnglish (official), Tok Pisin, Hiri M...

Leandro ChichizolaNazionalità Argentina Altezza185 cm Peso80 kg Calcio RuoloPortiere Squadra Parma CarrieraSquadre di club1 2009-2014 River Plate30 (-23)2014-2017 Spezia126 (-119)[1]2017-2018 Las Palmas27 (-47)2018-2021 Getafe1 (-1)2021 FC Cartagena9 (-10)2021-2022 Perugia38 (-32)[2]2022- Parma54 (-46)[3] 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasfe...

French classical composer (1862–1918) Debussy redirects here. For other uses, see Debussy (disambiguation). Debussy c. 1900 by Atelier Nadar (Achille) Claude Debussy[n 1] (French: [aʃil klod dəbysi]; 22 August 1862 – 25 March 1918) was a French composer. He is sometimes seen as the first Impressionist composer, although he vigorously rejected the term. He was among the most influential composers of the late 19th and early 20th centuries. Born to a family of mo...

City in Colorado, United States Home rule city in Colorado, United StatesGolden, ColoradoHome rule city[1]Downtown Golden, Colorado FlagMotto: Where the West LivesLocation of the City of Golden in Jefferson County, ColoradoGoldenLocation of the City of Golden in the United StatesCoordinates: 39°44′49″N 105°12′39″W / 39.74694°N 105.21083°W / 39.74694; -105.21083Country United StatesState ColoradoCountyJefferson County seat[1]Fo...

Irish appreciation of and contributions to the rock music genre Rock music in IrelandOther namesIrish rockStylistic originsRock musicRock and roll musicCultural originsIn the 1960s and the 1970s in Ireland Part of a series of articles onPopular music in Ireland Genres Rock Rebel Hip hop Jazz Artists Bands Albums Songs Charts Producers Awards Choice Music Prize IMRO Live Music Venue of the Year Awards Irish Music Television Awards Meteor Music Awards Competitions Eurosonic Festivals Current fe...

French composer, performer and record producer (born 1948) Jean-Michel JarreJarre in 2017Background informationBirth nameJean-Michel André JarreBorn (1948-08-24) 24 August 1948 (age 75)Lyon, FranceGenresAmbientnew-ageelectronictranceprogressive rock[1]technoOccupationsComposerperformerrecord producerInstrumentsSynthesizerpianoorganlaser harpaccordionguitarbass guitarthereminkeytarYears active1960–presentLabelsDisques DreyfusBMGSonyPolydorPolyGramEpicSMEWarner Bros.EMISpouse(s)...

كامبايلوس-بارافينتوس (بالإسبانية: Campillos-Paravientos)[1] - بلدية - تقسيم إداري البلد إسبانيا [2] المقاطعة قونكة خصائص جغرافية إحداثيات 39°58′24″N 1°32′47″W / 39.9734066°N 1.5465215°W / 39.9734066; -1.5465215 [3] [4] المساحة 54.34 كيلومتر مربع الارتفاع 11...

Gulliver and a giant, a painting by Tadeusz Pruszkowski (National Museum in Warsaw). The cultural influence of Gulliver's Travels has spanned centuries. Cultural influences From 1738 to 1746, Edward Cave published in occasional issues of The Gentleman's Magazine semi-fictionalized accounts of contemporary debates in the two Houses of Parliament under the title of Debates in the Senate of Lilliput. The names of the speakers in the debates, other individuals mentioned, politicians and monarchs...