ýÿñýØ╝Ùƒ¼ Ù▓¢ÙÅî
|
Read other articles:
Questa voce sull'argomento province della Thailandia ├¿ solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Prachuap Khiri KhanprovinciaÓ©øÓ©úÓ©░Ó©êÓ©ºÓ©ÜÓ©äÓ©ÁÓ©úÓ©ÁÓ©éÓ©▒Ó©ÖÓ©ÿÓ╣î LocalizzazioneStato Thailandia RegioneCentrale AmministrazioneCapoluogoDistretto di Mueang Prachuap Khiri Khan TerritorioCoordinatedel capoluogo11┬░49ÔÇ▓N 99┬░48ÔÇ▓E / 11.816667┬░N 99.8┬░E11.816667; 99.8´╗┐ (Prachuap Khiri Khan)Coordinate: 11┬░49ÔÇ▓N 99┬░48´┐¢...

For other uses, see Grae. 2020 studio album by Moses SumneyGræStudio album by Moses SumneyReleasedMay 15, 2020 (2020-05-15)Genre Art pop[1] art rock[2][3] avant-jazz[4][5] classical[2][6] folk[1][2][6] Length65:44LabelJagjaguwarProducer Moses Sumney Adult Jazz Ben Baptie John Congleton FKJ Daniel Lopatin Matthew Otto Moses Sumney chronology Aromanticism(2017) Græ(2020) Singles from Græ Vi...

Ϻ┘äÏ╣┘äϺ┘éϺϬ Ϻ┘ä┘êÏ│ÏÀ Ïú┘üÏ▒┘è┘é┘èÏ® Ϻ┘äÏ│┘èÏ▒Ϻ┘ä┘è┘ê┘å┘èÏ® ϼ┘à┘ç┘êÏ▒┘èÏ® Ïú┘üÏ▒┘è┘é┘èϺ Ϻ┘ä┘êÏ│ÏÀ┘ë Ï│┘èÏ▒Ϻ┘ä┘è┘ê┘å ϼ┘à┘ç┘êÏ▒┘èÏ® Ïú┘üÏ▒┘è┘é┘èϺ Ϻ┘ä┘êÏ│ÏÀ┘ë Ï│┘èÏ▒Ϻ┘ä┘è┘ê┘å ϬÏ╣Ï»┘è┘ä ┘àÏÁÏ»Ï▒┘è - ϬÏ╣Ï»┘è┘ä Ϻ┘äÏ╣┘äϺ┘éϺϬ Ϻ┘ä┘êÏ│ÏÀ Ïú┘üÏ▒┘è┘é┘èÏ® Ϻ┘äÏ│┘èÏ▒Ϻ┘ä┘è┘ê┘å┘èÏ® ┘ç┘è Ϻ┘äÏ╣┘äϺ┘éϺϬ Ϻ┘äϽ┘åϺϪ┘èÏ® Ϻ┘äϬ┘è Ϭϼ┘àÏ╣ Ï¿┘è┘å ϼ┘à┘ç┘êÏ▒┘èÏ® Ïú┘üÏ▒┘è┘é┘èϺ Ϻ┘ä┘êÏ│ÏÀ┘ë ┘êÏ│┘èÏ▒Ϻ┘ä┘è┘ê┘å.[1][2][3][4][...

V-1570 A V-1570-53 at the National Air and Space Museum. Type V12 piston engine Manufacturer Curtiss Aeroplane and Motor Company First run 1926 The Curtiss V-1570 Conqueror was a V12 liquid-cooled aircraft engine. Representing a more powerful version of the Curtiss D-12, the engine entered production in 1926 and flew in numerous aircraft.[1] Design and development Designed in 1924 as a military successor to the Curtiss D-12, initially named the Conqueror, it was later given the milit...

J65 Mesin Wright J65 Type Pancar Gas National origin Amerika Serikat Manufacturer Curtiss-Wright First run 1 Oktober 1948 (Sapphire) Maret 1951 (J65)[1] Major applications A-4 SkyhawkGrumman F-11 TigerMartin B-57 CanberraRepublic F-84F Thunderstreak Developed from Armstrong Siddeley Sapphire Wright J65 adalah sebuah mesin pesawat udara pancar gas yang diproduksi oleh Curtiss-Wright dengan lisensi dari Armstrong Siddeley. Pengembangannya adalah dinamakan Sapphire, dimana mesin ini men...

American basketball player (born 1998) Malik MonkMonk with the Los Angeles Lakers in 2022No. 0 ÔÇô Sacramento KingsPositionShooting guardLeagueNBAPersonal informationBorn (1998-02-04) February 4, 1998 (age 26)Jonesboro, Arkansas, U.S.Listed height6 ft 3 in (1.91 m)Listed weight200 lb (91 kg)Career informationHigh school East Poinsett(Lepanto, Arkansas) Bentonville(Bentonville, Arkansas) CollegeKentucky (2016ÔÇô2017)NBA draft2017: 1st round, 11th overall p...

This article is about the Moste District. For the former village of Moste, see Moste (Ljubljana). District in Upper Carniola, SloveniaMoste District ─îetrtna skupnost MosteDistrictMap of districts in Ljubljana. The Moste District is number 7.Moste DistrictLocation in SloveniaCoordinates: 46┬░04ÔÇ▓07ÔÇ│N 14┬░32ÔÇ▓02ÔÇ│E / 46.06861┬░N 14.53389┬░E / 46.06861; 14.53389Country SloveniaTraditional regionUpper CarniolaStatistical regionCentral SloveniaMunicipalityLjubljanaAre...

Pour les articles homonymes, voir Coppola et Ford (homonymie). Ne doit pas ├¬tre confondu avec Francis Ford. Pour les autres membres de la famille, voir Famille Coppola. Francis Ford Coppola Francis Ford Coppola en 2011. Donn├®es cl├®s Naissance 7 avril 1939 (85 ans)D├®troit, Michigan, ├ëtats-Unis Nationalit├® Am├®ricaine Profession R├®alisateurProducteur de cin├®maSc├®nariste Films notables Le Parrain (trilogie) Conversation secr├¿te Apocalypse Now Outsiders Dracula modifier Francis Fo...

American businessperson Emmett ShearShear in 2018Born1983 (age 40–41)Alma materYale University (BS)Known forCo-founder of TwitchFormer interim CEO of OpenAI Emmett Shear (born 1983) is an American Internet entrepreneur and investor.[1][a] He is the co-founder of live video platform Justin.tv. He served as the chief executive officer of Twitch when it was spun off from Justin.tv until March 2023. In 2011, Shear was appointed as a part-time partner at ventur...

Vidhan Sabha constituencyNarkatiaganjConstituency No. 3 for the Bihar Legislative AssemblyConstituency detailsCountryIndiaRegionEast IndiaStateBiharDistrictWest ChamparanLS constituency1. Valmiki NagarEstablished2008Total electors265,561ReservationNoneMember of Legislative Assembly17th Bihar Legislative AssemblyIncumbent Rashmi Varma PartyBJPAllianceNDAElected year2020 27┬░06ÔÇ▓20ÔÇ│N 84┬░27ÔÇ▓57ÔÇ│E / 27.10556┬░N 84.46583┬░E / 27.10556; 84.46583 Narkatiaganj Assembly ...

Canadian lay Catholic organization Catholic Civil Rights LeagueAbbreviationCCRLFormation1985TypeReligious organizations based in CanadaLegal statusactivePurposelobbying, courts, and media relationsHeadquartersOttawa, OntarioRegion served CanadaOfficial language EnglishFrenchWebsiteOfficial website This article is part of a series onConservatism in Canada Schools Calgary School Clerico-nationalism Right-wing populism Trumpism Social conservatism Social credit Toryism Blue Red Principles Canadi...

Municipality in Centre-Val de Loire, France For other uses, see Vendome (disambiguation). Subprefecture and commune in Centre-Val de Loire, FranceVend├┤meSubprefecture and communeView of Vend├┤me FlagCoat of armsLocation of Vend├┤me Vend├┤meShow map of FranceVend├┤meShow map of Centre-Val de LoireCoordinates: 47┬░47ÔÇ▓37ÔÇ│N 1┬░03ÔÇ▓59ÔÇ│E / 47.7936┬░N 1.0664┬░E / 47.7936; 1.0664CountryFranceRegionCentre-Val de LoireDepartmentLoir-et-CherArrondissementVend├┤meCantonVen...
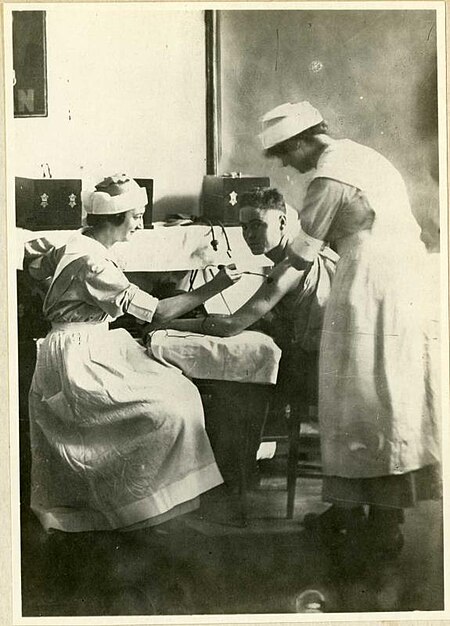
Elektrotopi atau Elektroterapi, penggunaan arus listrik bolak-balik untuk memberikan terapi kepada pasien Elektroterapi yaitu penggunaan alat terapi dengan memberikan arus bolak-balik pada tubuh manusia yang frekuensinya lebih dari 500.000 putaran per detik, akan tetapi tidak memberikan rangsangan terhadap saraf sensorik dan motorik.[1] Sumber lain menjelaskan bahwa elektroterapi adalah penggunaan arus listrik untuk perawatan medis.[2] Pada tahun 1855, Guillaume Duchenne yang ...

┘çÏ░┘ç Ϻ┘ä┘à┘éϺ┘äÏ® ┘èϬ┘è┘àÏ® ÏÑÏ░ ϬÏÁ┘ä ÏÑ┘ä┘è┘çϺ ┘à┘éϺ┘äϺϬ ÏúÏ«Ï▒┘ë ┘é┘ä┘è┘äÏ® ϼϻ┘ïϺ. ┘üÏÂ┘ä┘ïϺÏî Ï│ϺÏ╣Ï» Ï¿ÏÑÏÂϺ┘üÏ® ┘êÏÁ┘äÏ® ÏÑ┘ä┘è┘çϺ ┘ü┘è ┘à┘éϺ┘äϺϬ ┘àϬÏ╣┘ä┘éÏ® Ï¿┘çϺ. (ÏúÏ¿Ï▒┘è┘ä 2019) ┘ä┘è┘å┘è ┘àϺ┘â┘ä┘èÏ│ϬÏ▒ ┘àÏ╣┘ä┘ê┘àϺϬ Ï┤Ï«ÏÁ┘èÏ® Ϻ┘ä┘à┘è┘äϺϻ 13 ┘è┘åϺ┘èÏ▒ 1972 (52 Ï│┘åÏ®) Ï¿┘èϬÏ│Ï¿Ï▒Ï║ ┘à┘êϺÏÀ┘åÏ® Ϻ┘ä┘ê┘äϺ┘èϺϬ Ϻ┘ä┘àϬϡϻϮ Ϻ┘äÏ¡┘èϺϮ Ϻ┘äÏ╣┘à┘ä┘èÏ® Ϻ┘ä┘àÏ»Ï▒Ï│Ï® Ϻ┘äÏú┘à ┘â┘ä┘èÏ® Ï»┘è┘ü┘èÏ»Ï│┘ê┘å [┘äÏ║ϺϬ ÏúÏ«...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Human trafficking in Burkina Faso ÔÇô news ┬À newspapers ┬À books ┬À scholar ┬À JSTOR (December 2010) T...

Questa voce sull'argomento Tokyo ├¿ solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Suginamiquartiere specialeµØëõ©ªÕî║ Suginami ÔÇô Veduta LocalizzazioneStato Giappone RegioneKant┼ì Prefettura Tokyo SottoprefetturaNon presente DistrettoNon presente AmministrazioneSindacoSatoko Kishimoto dall'11-7-2022 TerritorioCoordinate35┬░41ÔÇ▓58ÔÇ│N 139┬░38ÔÇ▓11ÔÇ│E35┬░41ÔÇ▓58ÔÇ│N, 139┬░38ÔÇ▓11ÔÇ│E´╗┐ (Suginami) Superficie34,06 km┬▓ Abitanti589 528...

1945 film by Bodil Ipsen, Lau Lauritzen The Red Meadows1945 movie poster by Kai RaschDirected byBodil IpsenLau Lauritzen Jr.Written byLech FischerOle Juul (book)Produced byJens DennowHenning KarmarkStarringPoul ReichhardtLisbeth MovinCinematographyRudolf FrederiksenEdited byMarie EjlersenMusic bySven GyldmarkDistributed byASA FilmRelease date 1945 (1945) Running time85 minutesCountryDenmarkLanguageDanish The Red Meadows (Danish: De r├©de enge) is a 1945 Danish war drama directed by Bodil...

Coppa del Brasile 2018Copa do Brasil 2018 Competizione Coppa del Brasile Sport Calcio Edizione 30ª Organizzatore CBF Date dal 30 gennaio 2018al 17 ottobre 2018 Luogo Brasile Partecipanti 91 Risultati Vincitore Cruzeiro(6º titolo) Secondo Corinthians Cronologia della competizione 2017 2019 Manuale La Coppa del Brasile 2018 (ufficialmente in portoghese Copa do Brasil 2018) è stata la 30ª edizione della Coppa del Brasile. Indice 1 Formula 2 Partecipanti 2.1 Qualifi...

Sporting event delegationSouth Africa at the2015 World Aquatics ChampionshipsFlag of South AfricaFINA codeRSANational federationSwimming South AfricaWebsitewww.swimsa.co.zain Kazan, RussiaCompetitors43 in 5 sportsMedalsRanked 11th Gold 2 Silver 3 Bronze 0 Total 5 World Aquatics Championships appearances197319751978198219861991199419982001200320052007200920112013201520172019202220232024 South Africa competed at the 2015 World Aquatics Championships in Kazan, Russia from 24 July to 9 August 20...

French upper house from 1814 to 1848 For other uses, see Chamber of Peers. Chamber of Peers Chambre des PairsTypeTypeUpper house of the French Parliament HistoryFoundedJune 4, 1814 (1814-06-04)DisbandedFebruary 24, 1848 (1848-02-24)Preceded byS├®nat conservateurSucceeded bySenateStructurePolitical groupsUltra-royalistsLiberal royalistsRepublicansIndependentsDoctrinairesMeeting placeLuxembourg Palace, ParisConstitutionCharter of 1814Charter of 1815Charte...

















